Способы описания цифровых преобразователей

Цифровым преобразователем (ЦП) или цифровым фильтром называют вычислительное устройство, преобразующее входную числовую (импульсную) последовательность U*(kv) в выходную Y*(kv). Алгоритм функционирования ЦП с памятью, хранящей т входных и п выходных отсчетов, можно записать в виде соотношения, связывающего входные и выходные отсчеты,.

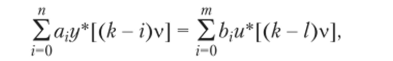
где a_v bj — коэффициенты, характеризующие алгоритм преобразования.

В большинстве приложений цифровые преобразователи работают с неизменным шагом дискретизации At = v, и для сокращения записи уравнений эту постоянную опускают. Тогда, приняв я₀ = 1 и выделив в левой части текущий отсчет при i = 0, представляют классическое описание алгоритма ЦП в более удобной форме.

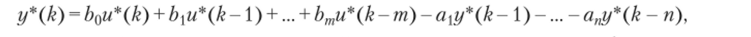
из которой следует, что выходной сигнал в момент времени kv определяется входной последовательностью т импульсов, а также последовательностью предшествующих (п- 1) выходных импульсов.

Приведенное уравнение «вход — выход» носит название разностного уравнения в неявной форме записи и может служить основой анализа и синтеза цифровых преобразователей. По заданному алгоритму ЦП можно реализовать программным способом на универсальном вычислительном оборудовании (ЦВМ) или с использованием типовых аппаратных средств. Для синтеза цифровых преобразователей используют следующий набор цифровых элементов: блок задержки на такт (запоминающее устройство), умножитель на постоянный коэффициент и цифровой сумматор (рис. 9.4).

Рис. 9.4. Элементы цифровых преобразователей:

а — задержка на такт; б — умножитель на постоянный коэффициент; в — цифровой сумматор Аппаратная реализация цифрового преобразователя возможна при выполнении условия т < п, свидетельствующего об отсутствии упреждающих звеньев, в которых реакция должна опережать по времени воздействие. Структура преобразователя (соединения элементов) определяется непосредственно способом записи алгоритма. Например, для ЦП второго порядка в соответствии с классической формой представления в виде.

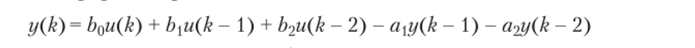
несложно синтезировать преобразователь с использованием приведенных элементов (рис. 9.5, а).

При построении цифровых преобразователей наряду с классической используют другие формы представления их уравнений.

Анализ процессов цифрового преобразования сигналов в системах с дискретным временем базируется на операциях с уравне;

Рис. 9.5. Структуры цифрового преобразователя:

а — классическая; б — каноническая ниями в конечных разностях, которые подобны производным в системах непрерывного времени:

• разность первого порядка (первая разность).

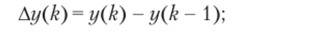
• разность второго порядка (вторая разность).

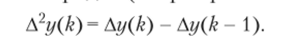
Вторую разность можно выразить через элементы последовательности.

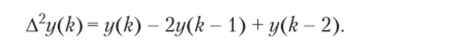
Вводят также разности более высокого порядка и выражают их через элементы последовательности.

С использованием конечных разностей можно перейти от основного соотношения цифрового фильтра к форме записи, подобной дифференциальному уравнению порядка п,

Полученное соотношение носит название уравнения в конечных разностях (разностного уравнения) порядка п.

При анализе цифровых преобразователей распространенной формой их описания служит система канонических разностных уравнений состояния, которую можно сформировать на основе классического уравнения ЦП путем замены переменных.

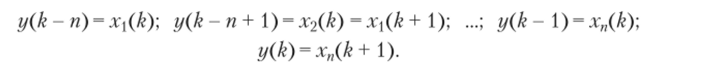
В результате получаем следующую систему уравнений:

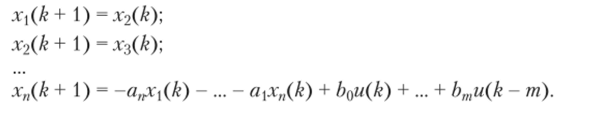
Форма записи уравнений определяет структуру программного алгоритма вычисления или аппаратной реализации ЦП с помощью типовых блоков (сумматора, умножителя, задержки).

В приведенной на рис. 9.5, а структуре, полученной с использованием классической записи уравнений, для задержки воздействия и выходного сигнала применены отдельные устройства. Схема имеет хорошую наглядность, но обладает аппаратной избыточностью вследствие использования четырех элементов задержки входного u (k) и выходного y (k) сигналов.

Для сокращения числа элементов уравнения ЦП приводят к канонической форме, в которой воздействие присутствует только в момент kv. Для этого вводят новую переменную к) и классическое уравнение переписывают в виде.

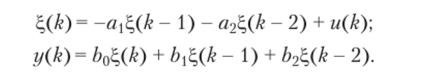
Переменные состояния можно выразить через новые величины, 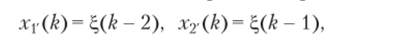и получить систему уравнений.

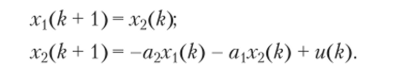
К этим уравнениям следует добавить уравнение выходной переменной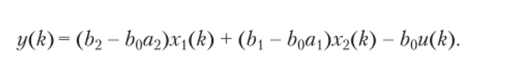

Приведенным уравнениям соответствует каноническая структура ЦП, содержащая всего два элемента задержки (рис. 9.5, б). Для преобразователей высокого порядка каноническая реализация позволяет существенно уменьшить аппаратные затраты, но сравнению с классической.

Применяется также синтез ЦП, но аналоговым прототипам, т. е. получение характеристик, которые сформулированы в терминах требований к аналоговой системе. Проиллюстрируем указанный подход на примере построения цифрового преобразователя, реализующего функциональные зависимости, аналогичные процессам в параллельном резонансном контуре (рис. 9.6, а).

Аналоговую цепь описывает система обыкновенных дифференциальных уравнений состояния

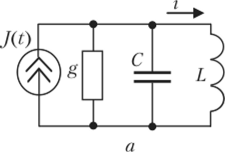
Рис. 9.6. Аналоговая схема (а) и ее цифровой эквивалент (б).

Разностные уравнения цифровой системы можно получить с использованием для производных приближенного соотношения.

Переход к обозначениям At = v и t = kv дает следующее аппроксимирующее выражение: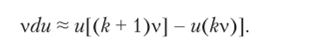

Замена производных в дифференциальных уравнениях на аппроксимирующие функции приводит к разностным уравнениям состояния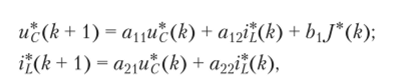

где а_п = (1 — Tg/C), а₂₂ = 1, а_{2 = -Т/С, а₂ = T/L, Ь = Т/С — коэффициенты (Т — длительность (время) тока).

Полученным разностным уравнениям состояния удовлетворяет структура ЦП (рис. 9.6, б), который в фиксированные моменты времени будет давать такие же значения выходного сигнала, как и в параллельном резонансном контуре при одинаковом воздействии.

В общем случае разностные уравнения состояния записывают в матричной форме: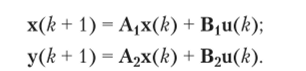

Приведенные соотношения применяют как для вывода общих свойств цифровых систем, так и для численного анализа преобразователей. В качестве переменных состояния обычно выбирают выходные сигналы элементов задержки, которые изменяются непрерывно и позволяют записать для них начальные условия.