Третий признак сравнения (признак сравнения со степенью)

Этот признак формулируется для произвольных (необязательно положительных) функций.

Теорема 4.18 (третий признак сравнения, или признак сравнения со степенью). 1. Для несобственных интегралов 1-го рода. Если при х —функция f является бесконечно малой функцией порядка р

по сравнению с бесконечно малой функцией —, т. е.

х

4−00.

то при р> 1 интеграл J f (x)dx сходится, а при р< 1 этот интеграл

а

расходится.

2. Для несобственных интегралов 2-го рода. Если при х—>Ь-0 функция /является бесконечно большой функцией порядка р по сравнению с бесконечно большой функцией —-, т. е.

Ь-х

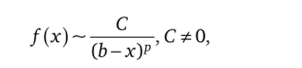
ь.

то при р < 1 интеграл J f (x)dx сходится, а при р> 1 — расходится.

а

Доказательство вытекает из теоремы сравнения и поведения инте;

+°° 1 ь ^.

тралов f —dx (а > 0) и f-dx, которые вычисляются явно при всех.

а ХР _аФ~х)Р

значениях параметра р.

Замечание 4.19. Третий признак сравнения относится к необходимым и достаточным условиям сходимости несобственных интегралов. Он дает ответ на вопрос о сходимости (расходимости) интеграла во всех случаях, когда применим. При этом если интеграл сходится по этому признаку, то он сходится абсолютно.

Пример 4.14.

Т dx

Исследовать сходимость интеграла J ,.

о 4х³ + х

Решение. Отметим, что данный интеграл является несобственным, так как на промежутке интегрирования имеются две особые точки: х = 0 (особенность 2-го рода, в окрестности этой точки подынтегральная функция не ограничена) и х = +°° (особенность 1-го рода). Используя свойство аддитивности, представим интеграл в виде суммы двух интегралов 7] и 1₂, так чтобы в каждом из полученных в результате интегралов осталось по одной особой точке:

• (в качестве, А можно взять любое положительное число), и исследуем сходимость каждого из них (интеграл 7 сходится тогда и только тогда, когда одновременно сходятся интегралы 7, и 7₂).
• 1. Исследуем сходимость интеграла 7,. При х —"+0 х «х³, поэтому подынтегральная функция. эквивалентна бесконечно большой функции сте- 1х³ + х

пенного видат= (являющейся главным членом подынтегральной функции), 4х

т. е.

и интегралы от них сходятся и расходятся одновременно. Так как-то по третьему признаку сравнения для интегралов 2-го рода интеграл 7, сходится.

2. Исследуем сходимость интеграла 7₂. При х —"оценим порядок малости подынтегральной функции:

(главный член подынтегральной функции), а значит, интегралы от этих функций сходятся и расходятся одновременно. Так как ³/₂ > 1, то по третьему признаку сравнения для интегралов 1-го рода интеграл 7, сходится.

Таким образом, так как интегралы 1_г и 7₂ сходятся, то сходится и их сумма — интеграл 7.

Исследовать сходимость интеграла f —.

о х^р

Решение. На промежутке интегрирования имеются две особые точки: х = О (особенность 2-го рода) и х = +°° (особенность 1-го рода). Представим интеграл в виде суммы двух интегралов 1_{ и 1₂, так чтобы в каждом из полученных в результате интегралов осталось по одной особой точке:

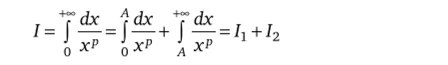
• (А > 0 — любое число), и исследуем сходимость каждого из них.
• 1. Интеграл Ij сходится при р < 1 и расходится при р > 1.
• 2. Интеграл 1₂ сходится при р > 1 и расходится при р < 1.

Таким образом, при любом р Ф1 один из интегралов или 1₂ сходится, а другой расходится, поэтому их сумма есть расходящийся интеграл. При р = 1 оба интеграла, а значит и их сумма, расходятся.

Ответ: интеграл расходится при любом р.

Т dx

Исследовать на сходимость интеграл -.

о хР + хЧ.

Решение. 1. Пусть р = q, тогда интеграл имеет вид i J — и, следовательно, расходится при любом р.

2. Пусть теперь p+°° /(х) =-= 0|—|, поэтому хР+хЧ 1хР/ ^к хР+хЧ v хЧ /

интеграл сходится тогда и только тогда, когда р < 1, q > 1.

3. Если p>q, то аналогичными рассуждениями получим, что интеграл сходится при р > 1, q < 1.

Итак, интеграл сходится тогда и только тогда, когда p±q, причем min (p, q) l.

Исследовать на сходимость интеграл

Решение. В окрестности точки х = а*, к = 1,2,…, п, подынтегральная функ;

(1)

ция /(х) есть О —, поэтому, чтобы интеграл сходился в окрест;

1|х-а*Р

ностях всех точек х = а_к, необходимо, чтобы p_fc < 1, к = 1,2,…, п. При х—>о°

( 1 1

имеем /(х)= О — —, следовательно, интеграл сходится при условии чМ^П™ у

Pi ⁺Р₂ ⁺-" + Рп >1Итак, интеграл сходится тогда и только тогда, когда р_к <1, к = 1,2,…, п,