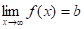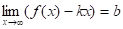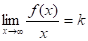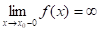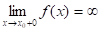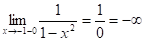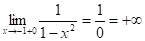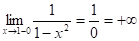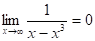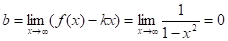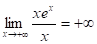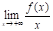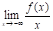Асимптоты графика функции

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки графика функции до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат.

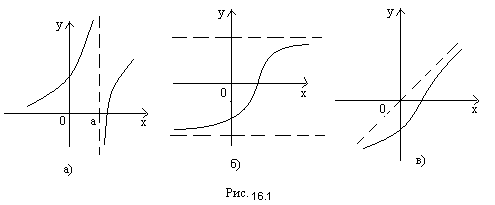
Асимптоты бывают вертикальными (рис. 1 а)), горизонтальными (рис. 1 б)), наклонными (рис. 1 в)).

Нахождение асимптот графика основано на следующих утверждениях.

Теорема 3. Пусть функция определена при достаточно больших х и существует конечный предел функции. Тогда прямая есть горизонтальная асимптота графика функции .

Если, то функция может иметь наклонную асимптоту.

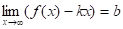
Теорема 4. Пусть функция определена при достаточно больших х и существуют конечные пределы функции и. Тогда прямая является наклонной асимптотой графика функции .

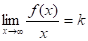
Теорема 5. Пусть функция определена в некоторой окрестности точки (исключая саму эту точку) и хотя бы один из пределов функции при х-0 (слева) или при х+0 (справа) равен бесконечности, т. е. или. Тогда прямая х = является вертикальной асимптотой графика функции .

Пример 3.

Найти асимптоты графика функции.

Решение Из области определения выпадают точки x = -1 и х = 1, т.к.

.

.

.

.

Следовательно, по теореме 5 прямые x = -1 и х = 1 являются вертикальными асимптотами.

Исследуем данную функцию на наклонную и горизонтальную асимптоты (теоремы 4 и 3).

k = ,.

y = 0-горизонтальная асимптота.

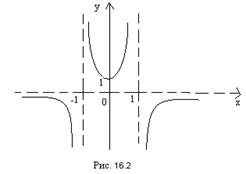
График функции изображен на рис. 2.

Ответ: x = -1 и х = 1 — вертикальные асимптоты, y = 0 — горизонтальная асимптота.

Пример 4.

Найти асимптоты графика функции.

Решение.

По теореме 16.4:

k = ,.

Следовательно при xграфик функции наклонной асимптоты не имеет.

При x:

k = ,.

b =.

график имеет горизонтальную асимптоту .