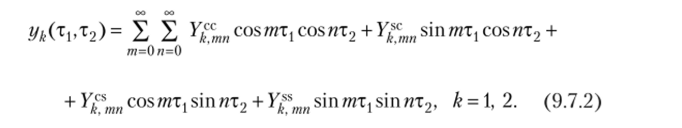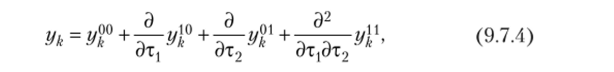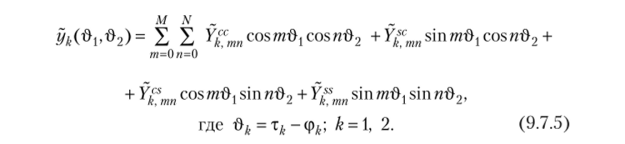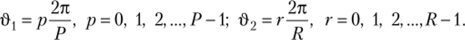Сущность метода идентификации при использовании двух ТС

При периодических воздействиях х{(т^)у х2(т2) отклики четырехполюсника могут быть представлены в виде двумерного тригонометрического ряда Фурье:

На основании (9.7.3) четырехполюсник можно описать следующим оператором:

Перепишем (9.7.2) в виде.

где г/^°, у™, г/? у^ — двумерные нелинейные функции независимых переменных х_и х₂. При этом первый член оператора (9.7.4) отражает безынерционные (статические) свойства НЧ, три последующих члена — инерционные (динамические) свойства НЧ, обусловленные изменяющимися во времени входным воздействием .r^ij), выходным воздействием х₂(т₂) и обоими воздействиями одновременно. Так как для ТС на интервале [0, л] существуют обратные функции, то после подстановки гДл^), т₂(х₂) в (9.7.3) можно получить аналитические выражения для характеристик оператора (9.7.4). Для ТС косинусоидальной формы (9.7.1) характеристики Ук°' Ук> Ук' у I' ^выражаются через полиномы Чебышёва первого рода. Для определения коэффициентов Y_k'_mn, Y™_mn, Y^_m", Y^_m" (9.7.3) искомых характеристик используется аппроксимирующий тригонометрический полином:

После подстановки &_к= т_к- фд, в (9.7.5) аппроксимирующий полином сводится к виду (9.7.2), что позволяет установить связь между коэффициентами Y_kpnn, Y_kpnn, Y?_mn, Yj^_m"

и Y^cc Y^sc Y^cs V^{55 и 1} k, mn> ¹ k, mtv ¹ k, mtv ¹ k, mrr

На частоты ТС введено ограничение в виде соотношения со,/со₂ = P/R целых чисел, не имеющих общего множителя. Исходными данными для определения коэффициентов полинома (9.7.5) служат отклики реального четырехполюсника в виде одномерных периодических функций г/Д&), где Э = соt; со = 2л/Г; ТРТ_{— RT₂. Для известных отсчетов одномерных откликов.

решается задача определения отсчетов у_крг откликов четырехполюсника, представленных в виде двумерных функций г/ДЗ, Э₂). В результате ее решения получены соотношения связи между аргументом i одномерных дискретных функций y_kj и аргументами/?, г двумерных дискретных функций у_крг. При этом область определения двумерных периодических функций у_к{0], Э₂) представляет собой равномерную сетку на квадрате, длина стороны которого равна 2я:

В работах [37, 48] выявлены особенности идентификации НЧ при использовании переменных и постоянных ТС. Даны сравнительная оценка обоих способов идентификации и рекомендации по их реализации. Рассмотрен вопрос о точности методов идентификации и приведены другие формы операторов (9.7.4). Возможности метода идентификации проиллюстрированы па конкретном примере.