Определение собственных частот системы с п степенями свободы

Отметим частные случаи матричного уравнения движения стержневой системы [см. (24.3)]: {ДО} ⁼ 0 — свободные затухающие колебания; {ДО} = 0 и [Я] = 0 — свободные незатухающие колебания.

Решение уравнения движения системы с одной степенью свободы показывает, что колебательное движение происходит по синусоиде:

Для определения собственных частот колебаний системы рассмотрим решение уравнения (24.3) для свободных незатухающих колебаний:

Выражение (24.9) можно использовать, лишь приняв следующую гипотезу: частота и фаза колебаний по всем направлениям одинаковы.

Эта гипотеза справедлива, если жесткости всех элементов системы отличаются нс слишком сильно. Представьте, что вы качаете дерево, толкая его ствол. Каждая ветка дерева будет колебаться со своей частотой, невпопад с колебаниями ствола, и принятая гипотеза в этом случае несправедлива. Подставим выражение (24.9) в уравнение движения (24.8). Для этого вычислим вторую производную от перемещений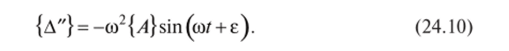

Выражение (24.10) справедливо при выполнении еще одной гипотезы: распределение скоростей и ускорений при колебательном движении системы пропорционально распределению перемещений при статическом приложении нагрузки.

Эта гипотеза становится несправедливой при больших частотах колебаний, когда велико влияние сил инерции.

Подставим выражения (24.9) и (24.10) в уравнение (24.8): — [М]аг{Л} sin (w/ + e) + [А']{/1 }sin (w/ + e) = 0. Сократив синус в последнем выражении, получаем:

и = y4sin (a)/+?). Примем условие, что и все узловые перемещения системы с п степенями свободы происходят по синусоиде:

Уравнение (24.11) в математике называется нестандартной или обобщенной задачей на собственные числа.

Напомним, что стандартная задача на собственные числа имеет вид ([/?]-Х[?"]){у4} = 0. Здесь [В] — симметричная положительно определенная матрица; X — собственное число; [?] — единичная матрица (аналог умножения матрицы на единицу); {А} — собственный вектор, соответствующий собственному числу X.

Примером решения стандартной задачи является определение главных напряжений: ([Г₀] — o_rnaB[E]){L} = 0, которое описано в п. 20.2.5. Стандартная задача решается методом вращений Якоби.

При решении нестандартной задачи тем же методом Якоби, надо, чтобы на месте матрицы масс находилась единичная матрица. Такое преобразование производится с использованием разложения матрицы [М] на верхнееи нижнетреугольную матрицы.

В силу принятых ранее гипотез, вследствие набегающей ошибки, лишь первые 4—5 компонентов вектора собственных частот действительно являются собственными частотами и совпадают с экспериментальными значениями. Остальные компоненты являются собственными числами, но не являются собственными частотами.

Рассмотрим пример испытаний консольной балки (пластмассовой линейки) на вибростенде (рис. 24.3). Собственный вектор {А} представляет собой форму колебаний, т. е. вид изогнутой оси балки в процессе колебаний. Экспериментальная максимальная амплитуда колебаний А_тгх резко уменьшается с ростом номера собственной частоты о). В то же время определить величину амплитуды колебаний расчетным путем невозможно, так как в системе уравнений (24.8) необходимо еще одно уравнение. Приходится задаваться А_х = 1. В результате находим лишь форму колебания, но не величину амплитуды колебаний. Для удобства сопоставления форм колебаний найденные амплитуды нормируются по длине многомерного вектора А.

А =. г. На выходе из программы расчета максимальные ампли;

' ,/х?

туды колебаний для всех собственных векторов примерно одинаковы.

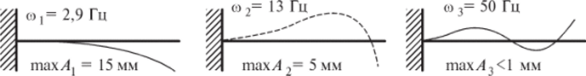
Рис. 24.3. Формы колебаний консольной балки на трех первых частотах.