Задачи. 
Дискретный анализ. 
Основы высшей алгебры

Некоторые из предлагаемых ниже задач очень просты и получаются немедленным применением приведенных в основном тексте рассуждений. Но есть и сложные задачи, которые требуют привлечения новых идей.

1.1. Является ли ассоциативной операция * на множестве положительных действительных чисел, задаваемая формулой.

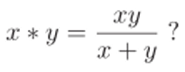
• 1.2. Построить пример неассоциативной бинарной операции, для которой выполняются аксиома единицы и аксиома обратного элемента.
• 1.3. Доказать, что конечное множество G, в котором определена ассоциативная алгебраическая операция и каждое из уравнений ах = Ъ, уа = b дня любых а и b из G имеет в G единственное решение, будет группой.
• 1.4. Пусть в полугруппе G есть правая единица е (для любого х е G выполнено хе = я) и для любого х € G есть правый обратный х~¹ (х • аг^-1 = е). Доказать, что тогда G — группа (в частности, единица в пей единственна и для каждого элемента обратный тоже единственен).
• 1.5. Выяснить, образуют ли группы следующие множества при указанной операции над элементами:
• 1) целые числа относительно сложения;
• 2) четные числа относительно сложения;
• 3) целые числа, кратные данному натуральному числу п, относительно сложения;
• 4) степени данного действительного числа а, а ^ 0, ±1, с целыми показателями относительно умножения;
• 5) неотрицательные целые числа относительно сложения;
• 6) нечетные целые числа относительно сложения;
• 7) целые числа относительно вычитания;
• 8) рациональные числа относительно сложения;
• 9) рациональные числа относительно умножения;
• 10) рациональные числа, отличные от нуля, относительно умножения;
• 11) положительные рациональные числа относительно умножения;
• 12) положительные рациональные числа относительно деления;
• 13) двоично-рациональные числа, т. е. рациональные числа, знаменатели которых, — степени числа 2 с целыми неотрицательными показателями, относительно сложения;
• 14) все рациональные числа, знаменатели которых равны произведениям простых чисел из данного множества М (конечного или бесконечного) с целыми неотрицательными показателями (лишь конечное число которых может быть отлично от нуля), относительно сложения;
• 15) корни гг-й степени из единицы (как действительные, так и комплексные) относительно умножения;
• 16) корни всех целых положительных степеней из единицы относительно умножения;
• 17) матрицы порядка п с действительными элементами относительно умножения;
• 18) невырожденные матрицы порядка п с действительными элементами относительно умножения;
• 19) матрицы порядка п с целыми элементами относительно умножения;
• 20) матрицы порядка п с целыми элементами и определителем, равным 1 относительно умножения;
• 21) матрицы порядка п с целыми элементами и определителем, равным ±1 относительно умножения;
• 22) матрицы порядка п с действительными элементами относительно сложения;
• 23) перестановки чисел 1,2,…, п относительно композиции перестановок;
• 24) четные перестановки чисел 1,2,…, п относительно композиции перестановок;
• 25) нечетные перестановки чисел 1,2,…, п относительно композиции перестановок;
• 26) взаимно однозначные отображения множества натуральных чисел на себя, каждое из которых перемещает (отображает не в себя) лишь конечное число чисел, если за произведение отображений .s и t принята композиция sot отображений (последовательное выполнение отображений t, затем .s);
• 27) преобразования множества М, т. е. взаимно однозначные отображения этого множества на себя, относительно композиции отображений;
• 28) векторы n-мерного линейного пространства М^п относительно сложения;
• 29) параллельные переносы трехмерного пространства R'³ относительно композиции движений;
• 30) повороты трехмерного пространства R'⁵ вокруг прямых, проходящих через данную точку О относительно композиции движений;
• 31) все движения трехмерного пространства R³ относительно композиции движений;
• 32) положительные действительные числа относительно операции а *Ь = а^ь;
• 33) положительные действительные числа относительно операции а *Ь = а²Ь²
• 34) действительные многочлены степени не выше п от неизвестного х и нулевой многочлен относительно сложения;
• 35) действительные многочлены степени п от переменной х относительно сложения;
• 36) действительные многочлены любых степеней (включая 0) от переменной х относительно сложения;
• 37) отрезок [0,1] с операцией ф, где аф/3 дробная часть
• 38) множество функций вида

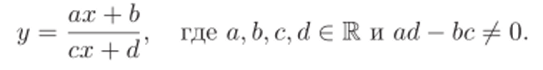
1.6. Доказать, что множество A]® так называемых аффинных преобразований: х ах + b (a, b € М; а ^ 0) вещественной прямой R образует группу с законом умножения ч>а, ъфсл = <�РасМ+Ь‘ В группе >li (IR) содержится подгруппа GL ( 1, R), оставляющая точку х = 0 на месте, и подгруппа «чистых сдвигов» х I—> х 4- Ь.

1.7. В любой ли группе выполняются тождества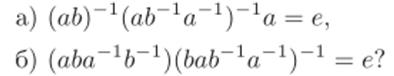

1.8. Для любых трех элементов а, 6, с группы G выполняется равенство.

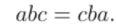
Верно ли, что группа коммутативная?

• 1.9. Пусть в группе G выполняется тождество а? а = е. Доказать, что G — коммутативная.
• 1.10*. Доказать, что группа корней п-й степени из единицы является единственной мультипликативной группой n-го порядка с комплексными элементами.
• 1.11*. Найти все (с точностью до изоморфизма) группы порядка а) 3; б) 4; в) б. Выписать таблицы умножения этих групп и представить эти группы в виде групп перестановок.
• 1.12. Доказать, что группы 1) — 4) задачи 1.5 изоморфны между собой.
• 1.13*. Доказать, что:
  • а) симметрическая группа S_n при п > 1 порождается транспозициями (12), (13), …, (In);
  • б) знакопеременная группа Л_п при п > 2 порождается множеством всех тройных циклов (ijk);
  • в) знакопеременная группа А_п при п > 2 порождается тройными циклами: (12 3), (12 4), (12п).
• 1.14. Найти минимальное количество перестановок п элементов, порождающих группу S_n, п ^ 3.
• 1.15. Найти порядок элемента

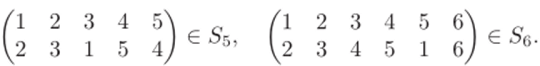
• 1.16. Существует ли в Sq элемент порядка 8?
• 1.17. Цикличиа ли группа С2 х С5?
• 1.18. В циклической группе (а) порядка п найти все элементы д, удовлетворяющие условию д^к = е, и все элементы порядка к при
• а) п = 24, к = 6;
• б) п = 100, к = 20;
• в) п = 100, к = 5;
• г) п = 360, к = 30;
• д) п = 360, к = 12;
• е) п = 360, к = 7.
• 1.19. Пусть G = (а) конечная циклическая группа порядка п. Доказать утверждения:
  • а) для любого делителя d числа п существует единственная подгруппа II группы G, имеющая порядок d
  • б) порождающими подгруппы Н порядка d являются все элементы порядка d группы G. В частности, Н = {aⁿ^^d).
• 1.20. Доказать, что если элемент х группы G имеет бесконечный порядок, то х^к = х^т тогда и только тогда, когда к = т.
• 1.21. Доказать, что если е — единица и а — элемент порядка п группы G, то а^к = е тогда и только тогда, когда к делится на п.
• 1.22. Найти порядок элемента х^к, если порядок элемента х равен п.
• 1.23. Доказать утверждения:
  • а) если элементы а и b группы G перестановочны (коммутируют), т. е.

и имеют конечные взаимно простые порядки г и 5, то их произведение ab имеет порядок rs

б) если элементы а и b группы G перестановочны, имеют конечные порядки г и .s и пересечение порожденных ими циклических подгрупп содержит лишь единицу е, т. е.

то порядок произведения ab равен наименьшему общему кратному г и s. Показать на примерах, что для справедливости последнего утверждения каждого из условий (1°) и (2°) в отдельности недостаточно и что условие (1°) не является следствием условия (2°), даже для взаимно простых порядков элементов а и Ь:

• в) если порядки г и s элементов а и b взаимно просты, то условие (2°) выполняется;
• г) показать на примере, что без условия (2°) порядок произведения ab не определяется однозначно порядками сомножителей а и Ь.
• 1.24. Пусть G = (а) — циклическая группа порядка п. Доказать, что:
  • а) если n и к взаимно просты, то в G существует корень т. е. а является к-й степенью некоторого элемента из G и обратно;
• 5) в группе нечетного порядка все элементы являются квадратами.
• 1.25. Пусть порядок элемента х группы G есть число pry, где р и q — взаимно просты. Доказать, что в группе G найдутся такие элементы и и с, что выполняются равенства

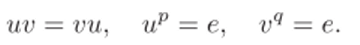
• 1.26*. Доказать, что если в конечной группе G порядка п для каждого делителя d числа п уравнение x^d = е имеет не более d решений, то группа G — циклическая.
• 1.27*. Показателем группы назовем наименьшее общее кратное порядков ее элементов. Доказать, что коммутативная группа циклическая тогда и только тогда, когда показатель равен порядку группы.
• 1.28. Какие из групп задачи 1.5 являются подгруппами других из этих групп?
• 1.29. Доказать, что любая бесконечная группа имеет бесконечное число подгрупп.
• 1.30. Найти с точностью до изоморфизма все группы, которые изоморфны любой своей неедииичиой подгруппе.
• 1.31. Найти все подгруппы:
  • а) циклической группы порядка 6;
• 6) циклической группы порядка 24;
• в) четверной группы (задача 1.11);
• г) симметрической группы SY
• д) Какие из подгрупп группы S3 являются нормальными делителями?
• е) Доказать, что знакопеременная группа четвертой степени А не имеет подгруппы шестого порядка. Таким образом, группа G порядка п для некоторых к, делящих п, может не иметь подгрупп порядка к.
• 1.32. Найти все подгруппы группы G порядка 8, все элементы которой, кроме единицы е, имеют порядок 2.
• 1.33. Найти все подгруппы циклической группы порядка р^п, где р — простое число.
• 1.34. Найти смежные классы
• а) аддитивной группы целых чисел по подгруппе чисел, кратных данному натуральному числу d
• б) аддитивной группы действительных чисел по подгруппе целых чисел;
• в) аддитивной группы комплексных чисел по подгруппе целых гауссовых чисел, т. е. чисел вида т + /гг, т, п Е Z;
• г) аддитивной группы векторов плоскости (выходящих из начала координат) но подгруппе векторов, лежащих на оси Ох:
• д) мультипликативной группы комплексных чисел, отличных от нуля, по подгруппе чисел, равных по модулю единице;
• е) мультипликативной группы комплексных чисел, отличных от нуля, по подгруппе положительных действительных чисел;
• ж) мультипликативной группы комплексных чисел, отличных от нуля, по подгруппе действительных чисел;
• з) симметрической группы S_n но подгруппе перестановок, оставляющих число п на месте.
• 1.35. Доказать, что
• а) если Я — конечное множество элементов группы G и произведение двух любых элементов из Я снова лежит в Я, то Н :
• б) если все элементы множества Я группы G имеют конечные порядки и произведение двух любых элементов из Я снова лежит в Я, то Я будет подгруппой группы G.
• 1.36. Найти центр у группы обратимых действительных матриц размера п х п.
• 1.37. Сколько подгрупп второго порядка имеет группа Sr,?
• 1.38. Есть ли подгруппа индекса 2 в Л_п?
• 1.39. Периодической частью группы G называется множество всех ее элементов конечного порядка. Доказать, что периодическая часть коммутативной группы является подгруппой.
• 1.40. Доказать, что если в коммутативной группе G есть элементы бесконечного порядка, и все они содержатся в подгруппе Я, то Я = G.
• 1.41*. Доказать, что подгруппа Я индекса два любой группы G содержит квадраты всех элементов группы G.
• 1.42*. Доказать, что при п > 1 знакопеременная группа А_п является единственной подгруппой индекса два в симметрической группе S_n. Привести пример конечной группы, содержащей несколько подгрупп индекса два.
• 1.43. Доказать, что:
  • а) группа положительных действительных чисел по умножению изоморфна группе всех действительных чисел по сложению;
  • б) группа положительных рациональных чисел по умножению не изоморфна группе всех рациональных чисел по сложению.
• 1.44. Доказать, что в коммутативной группе множество элементов, порядки которых делят фиксированное число, является подгруппой. Верно ли это утверждение для некоммутативной группы?
• 1.45. Доказать, что группа G' является гомоморфным образом конечной циклической группы G тогда и только тогда, когда G' также циклическая и ее порядок делит порядок группы G.
• 1.46. Доказать, что если группа G гомоморфно отображена

на группу G', причем а а', то.

• а) порядок а делится на порядок а!
• б) порядок G делится па порядок G'.
• 1.47. Доказать, что порядок любой нечетной перестановки в S_n четен.
• 1.48. Найти все гомоморфные отображения а) циклической группы С_п в себя; б) С₆ в Ci₈; в) С_]8 в С₆; г) С₂ в С]₅; д) С₆ в С₂->.
• 1.49. Доказать, что аддитивную группу ради опальных чисел нельзя гомоморфно отобразить на аддитивную группу целых чисел.
• 1.50. Пусть р — простое число. Изоморфны ли группы C_pi иС_рх С_р?
• 1.51. Изоморфны ли группы а) С$ х С₂о и С₂ х С30; б) Gig х С20 и С36 х Сю?
• 1.52. Сколько подгрупп, изоморфных С4, содержится в С12 X С]8?
• 1.53*. Доказать, что:
  • а) группа тетраэдра изоморфна группе четных перестановок четырех элементов;
  • б) группы куба и октаэдра изоморфны группе всех перестановок четырех элементов;
  • в) группы додекаэдра и икосаэдра изоморфны группе четных перестановок пяти элементов.
• 1.54. Пусть в конечной группе G выполняется тождество а — а = е. Доказать, что эта группа изоморфна группе подмножеств конечного множества относительно операции симметрической разности: А ф В = (А В) U (В А).
• 1.55. Сколько есть разных ожерелий из 2 красных, 2 зеленых и 2 желтых бусин? (Определение разных ожерелий см. в примере 1.55.)
• 1.56. Является ли нормальной подгруппа симметрической группы S_n, которая содержит все перестановки, оставляющие число п на месте?
• 1.57. Является ли нормальной подгруппой в Sio группа перестановок, которые каждое четное число оставляют на месте?
• 1.58. Доказать, что в любой группе перестановок, содержащей хотя бы одну нечетную перестановку:
  • а) число четных перестановок равно числу нечетных;
  • б) четные перестановки образуют нормальный делитель;
  • в) все простые группы перестановок п элементов (где п > 2) содержатся в знакопеременной группе А_п (простой называется группа, не имеющая нормальных делителей, кроме себя самой и единичной подгруппы).
• 1.59. Доказать, что центр группы G (пример 1.18 на с. 25) является нормальным делителем.
• 1.60. Элемент аЬа~¹Ь~¹ называется комм г/т, а тор ом элементов а и b группы G. Доказать, что группа К, порожденная коммутаторами всех пар элементов группы, является нормальной подгруппой К группы G. Эта подгруппа называется коммутантом G.
• 1.61. Доказать, что любая четная перестановка является коммутатором некоторых перестановок. Найти коммутант симметрической группы S_n.
• 1.62. Привести пример группы, в которой коммутант нс совпадает с множеством коммутаторов.
• 1.63. Пусть G — группа всех собственных движений трехмерного пространства, Н — подгруппа параллельных переносов, К — подгруппа вращений, оставляющих неподвижной точку О. Доказать, что
• а) Я является нормальным делителем G, а К — нет;
• б) факторгруппа G/Н изоморфна К.
• 1.64. Доказать, что нормальный делитель группы G, имеющий конечный индекс к, содержит все элементы группы G, порядки которых взаимно просты с к. Показать на примере, что для подгруппы Я, не являющейся нормальным делителем, утверждение может быть неверным.
• 1.65. Доказать, что факторгруппа G/H тогда и только тогда коммутативна, когда Я содержит коммутант К группы G.
• 1.66. Доказать, что во всякой группе элементы х и уху~¹ имеют один и тот же порядок.
• 1.67. Доказать, что для любых элементов а, 6 и с группы G:
  • а) элементы ab и Ьа имеют одинаковый порядок;
  • б) элементы abc, Ьса и cab имеют одинаковый порядок.
• 1.68. Построить пример группы, в которой есть такие элементы а, 6, с, что abc и eba имеют разный порядок.
• 1.69*. Доказать, что:
  • а) четверная группа V (задача 1.11) является нормальным делителем симметрической группы S4;
  • б) факторгруппа S4/V изоморфна симметрической группе S3.
• 1.70*. Найти число перестановок симметрической группы S_n, коммутирующих с данной перестановкой о.
• 1.71*. Доказать, что если пересечение двух нормальных делителей Я1 и Н2 группы G содержит лишь единицу е, то hli2 = fi2h для всех элементов h € Н%, h₂ G Я₂.
• 1.72. Пусть в группе G подгруппа N (a) является нормализатором элемента а. Показать, что для любого х € G нормализатором элемента яад:^-1 будет, тЛ^г(а)а:^-1.
• 1.73. Пусть N = N (H) — нормализатор подгруппы Я в группе G. Дано правое разложение G по N (H):

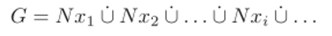
Доказать, что все множества

различны и что всякое множество, сопряженное с Я, совпадает с одним из XjHx~ (г = 1,2,…).

• 1.74. Доказать, что
• а) нормализатор N (a) содержит подгруппу (а) в качестве нормального делителя;
• б) число элементов группы G, сопряженных с а, равно индексу нормализатора N (а) в G.
• 1.75. Доказать, что
• а) нормализатор N (H) подгруппы Я в группе G содержит подгруппу Я в качестве нормального делителя;
• б) число подгрупп группы <7, сопряженных с Я, равно индексу нормализатора N (H) в G.
• 1.76. Доказать, что:
  • а) число элементов группы G, сопряженных с данным элементом, делит порядок группы G;
  • б) число подгрупп группы G, сопряженных с данной подгруппой, делит порядок группы G.
• 1.77. Пусть х — элемент конечной группы G и к — число элементов, сопряженных с х в G: пусть к' — число элементов, сопряженных с х^п в G. Доказать, что к! — делитель числа к.
• 1.78. Пусть Я — подгруппа индекса 2 в группе С, К — класс сопряженных в G элементов и К С Я. Доказать, что К является либо классом сопряженных в Я элементов, либо объединением двух классов сопряженных в Я элементов, состоящих из одинакового числа элементов.
• 1.79. Найти число перестановок симметрической группы S_n, сопряженных с данной перестановкой о.
• 1.80*. Конечная группа G имеет порядок р^п, где р — простое число. Доказать, что G имеет нетривиальный центр (содержащий более одного элемента).
• 1.81*. Доказать, что любой нормальный делитель А знакопеременной группы А_п степени п ^ 5, содержащий хотя бы один тройной цикл, совпадает с А_п.
• 1.82*. а) Найти все классы сопряженных элементов группы икосаэдра;
• б) доказать, что группа икосаэдра является простой (т. е. не имеет нормальных делителей, отличных от самой группы и единичной подгруппы).
• 1.83*. Доказать, что знакопеременная группа пятой степени является простой.
• 1.84. Доказать, что факторгруппа симметрической группы S_n по знакопеременной группе Л_п изоморфна факторгруппе аддитивной группы целых чисел по подгруппе четных чисел.
• 1.85. Построить факторгруппу
• а) аддитивной группы целых чисел по подгруппе чисел, кратных данному натуральному числу d;
• б) аддитивной группы целых чисел, кратных 3, но подгруппе чисел, кратных 15;
• в) аддитивной группы целых чисел, кратных 4, по подгруппе чисел, кратных 24;
• г) мультипликативной группы действительных чисел, отличных от нуля, по подгруппе положительных чисел;
• д) аддитивной группы комплексных чисел по подгруппе целых гауссовых чисел;
• е) аддитивной группы векторов плоскости (выходящих из начала координат) но подгруппе векторов, лежащих на оси Ох;
• ж) мультипликативной группы комплексных чисел, отличных от нуля, по подгруппе действительных чисел.
• 1.86. Пусть G_n — аддитивная группа векторов п-мерного линейного пространства и Яk — подгруппа векторов^{-мерного} подпространства, 0 ^ к ^ п. Доказать, что факторгруппа Grx/Нь изоморфна G_n-k-
• 1.87. Пусть G мультипликативная группа всех комплексных чисел, отличных от 0, и II — множество всех чисел из G, лежащих на действительной и мнимой осях.
• а) Доказать, что Я — подгруппа группы G.
• б) Найти смежные классы группы G по подгруппе Я.
• в) Доказать, что факторгруппа G/H изоморфна мультипликативной группе U всех комплексных чисел, равных по модулю 1.
• 1.88*. Пусть

G — мультипликативная группа комплексных чисел, отличных от О, Я — множество чисел из G, лежащих на п лучах, выходящих из 0 под равными углами, причем один из этих лучей совпадает с положительной действительной полуосью.

К — аддитивная группа всех действительных чисел,.

Z — аддитивная группа целых чисел,.

D — мультипликативная группа положительных чисел,.

U — мультипликативная группа комплексных чисел, равных по модулю 1,.

U_n — мультипликативная группа корней п-й степени из 1. Доказать, что.

a) K/Z * U; б) G/D ^ U; в) G/U ^ D:

• г) U/U_n = U; д) G/U_n = G; е) Н < G и G/H = U;
• ж) H/D = U_n з) H/U_n = D.
• 1.89. Для мультипликативных групп невырожденных квадратных матриц порядка п доказать утверждения:
  • а) факторгруппа группы действительных матриц по подгруппе матриц с определителем, равным 1, изоморфна мультипликативной группе действительных чисел, отличных от 0;
  • б) факторгруппа группы действительных матриц по подгруппе матриц с определителем, равным ±1, изоморфна мультипликативной группе положительных чисел;
  • в) факторгруппа группы действительных матриц по подгруппе матриц с положительными определителями является циклической группой второго порядка;
  • г) факторгруппа группы комплексных матриц по подгруппе матриц с определителями, по модулю равными 1, изоморфна мультипликативной группе положительных чисел;
  • д) факторгруппа группы комплексных матриц по подгруппе матриц с положительными определителями изоморфна мультипликативной группе комплексных чисел, по модулю равных 1.
• 1.90. Доказать, что в факторгруппе Q/Z (Q — аддитивная группа рациональных чисел, Z — аддитивная группа целых чисел):
  • а) каждый элемент имеет конечный порядок;
  • б) для каждого натурального п имеется в точности одна подгруппа порядка п.
• 1.91. Доказать, что
• а) симметрическая группа 5з имеет шесть внутренних автоморфизмов и ни одного внешнего, причем группа автоморфизмов изоморфна 5з;
• б) четверная группа V (задача 1.11) имеет один внутренний автоморфизм (тождественный) и пять внешних, причем группа автоморфизмов изоморфна S3.
• 1.92. Доказать, что для любой группы G множество всех внутренних автоморфизмов является нормальной подгруппой в группе всех автоморфизмов группы G.
• 1.93*. Существуют ли у Sq внешние автоморфизмы?
• 1.94. Доказать, что группа внутренних автоморфизмов группы G изоморфна факторгруппе группы G но ее центру.
• 1.95. Доказать, что группа всех автоморфизмов некоммутативной группы не может быть циклической.
• 1.96. Доказать, что факторгруппа некоммутативной группы по ее центру (пример 1.18 на с. 25) не может быть циклической.
• 1.97*. Доказать, что если порядок конечной группы G делится на простое число р, то G содержит элемент порядка р (теорема Коши).
• 1.98*. Пусть р — простое число. Г руина G называется />-группой, если порядки всех ее элементов конечны и равны некоторым степеням числа р. Доказать, что конечная группа G тогда и только тогда будет р-группой, когда ее порядок равен степени числа р.
• 1.99. Доказать, что группа порядка р², где р — простое число, коммутативна.
• 1.100. Найти число классов сопряженности и число элементов в каждом классе для пекоммутативной группы порядка р³, где р — простое число.
• 1.101. Доказать, что:
  • а) аддитивная группа векторов n-мерного линейного пространства есть прямая сумма п подгрупп векторов одномерных подпространств, натянутых на векторы любого базиса пространства;
  • б) аддитивная группа комплексных чисел есть прямая сумма подгрупп действительных и чисто мнимых чисел;
  • в) мультипликативная группа действительных чисел есть прямое произведение подгруппы положительных чисел и подгруппы чисел ±1;
  • г) мультипликативная группа комплексных чисел есть прямое произведение подгрупп положительных чисел и чисел, по

модулю равных единице.

• 1.102. Доказать, что если G = А + В = А + В-2 — прямые разложения абелевой группы G и В С Z?2, то В = В2-
• 1.103. Доказать, что прямое разложение G = Н+К абелевой группы G существует тогда и только тогда, когда существует гомоморфное отображение G на подгруппу Я, сохраняющее на месте все элементы из Я.
• 1.104. Доказать, что если G = А 4- В — прямое разложение группы G, то факторгруппа G/А изоморфна В.
• 1.105. Пусть G = А + А2 4- • • • 4- А_а разложение абелевой

группы G в прямую сумму подгрупп и х = (1 + а 2 + • • • + a_s, (ik € Ak, к = 1,2, — соответствующее разложение эле мента х в сумму компонент. Доказать, что:

• а) группа G тогда и только тогда имеет конечный порядок гг, когда каждая подгруппа Ak имеет конечный порядок п^, к = 1,2,…, s, причем п = пП2 … n_s.
• б) элемент тогда и только тогда имеет конечный порядок р, когда каждая его компонента а* имеет конечный порядок /д-, к = 1, 2,…, s, причем р равно наименьшему общему кратном}' чисел рир₂, • • •, Ps-
• в) группа G тогда и только тогда является конечной циклической, когда все прямые слагаемые Ak — конечные циклические группы, причем их порядки попарно взаимно просты.
• 1.106. Разложить в прямую сумму примарных компонент циклическую группу порядка: а) 6; б) 12; в) 60; г) 900.
• 1.107*. Доказать неразложимость в прямую сумму двух ненулевых подгрупп:
  • а) аддитивной группы целых чисел;
  • б) аддитивной группы рациоиапьиых чисел;
  • в) циклической группы порядка р^п, р простое.
• 1.108*. Пусть G — ненулевая конечная абелева группа (с аддитивной записью операции). Доказать утверждения:
  • а) если порядки всех элементов из G делят произведение pq взаимно простых чисел р и q, то G разлагается в прямую сумму подгрупп Л и Я, где порядки всех элементов из А делят р, а из В — делят q, причем одна из подгрупп А или В может оказаться нулевой;
  • б) для группы G имеет место разложение G = Л1+Л2−1-. .+ -I- A_s в прямую сумму ненулевых подгрупп, порядок элементов Ai — степень простого числа р, причем все р, различны: Pi Ф Рз при г ф 3
  • в) группа Afc, относящаяся к простому числу рь состоит из всех элементов группы G, порядки которых равны степеням числар^к, что однозначно определяет разложение из пункта б).
• 1.109. Найти все (с точностью до изоморфизма) абелевы группы следующих порядков:
  • а) 3; 6) 4; в) 6; г) 8; д) 9; е) 12; ж) 16; з) 24; и) 30; к) 36; л) 48; м) 60; н) 63; о) 72; и) 100.
• 1.110*. Разложить в прямую сумму примарных циклических и бесконечных циклических подгрупп факторгруппу Z³/Я, где a? i, х₂, #з ^— порождающие Z³, а порождающие II заданы

соотношениями.

• 1.111. Доказать, что является циклической конечная абелева группа G, порядок которой равен:
  • а) произведению двух различных простых чисел р и р;
  • б) произведению различных простых чисел Pi, Р2, • • •, Ps
  • в) найти все подгруппы абелевой группы G, порядок которой удовлетворяет условию пункта б), и найти число этих

подгрупп;

• г) доказать, что для любого делителя к порядка п конечной абелевой группы G существуют подгруппа и факторгруппа группы G, имеющие порядок к.
• 1.112. Пусть G — ненулевая конечная абелева группа, все ненулевые элементы которой имеют один и тот же порядок р (элементарная группа). Доказать утверждения:
  • а) число р является простым;
  • б) группа G разлагается в прямую сумму конечного числа циклических подгрупп порядка р и имеет порядок р^к, где к число этих слагаемых;
  • в) любая ненулевая подгруппа II группы G сама будет элементарной и является прямым слагаемым в некотором прямом разложении G = Н + К группы G:
  • г) число подгрупп порядка р³ элементарной группы G порядка р^к к ^ s > 0, равно

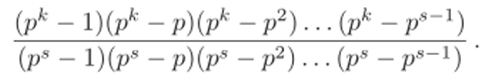
1.113. Доказать, что конечная абелева группа G порождается ее элементами максимального порядка.