Задачи.
Дискретный анализ.
Основы высшей алгебры

РефератПомощь в написанииУзнать стоимостьмоей работы

А) Доказать, что если многочлены f (x) и д (х) с целыми коэффициентами взаимно просты над полем вычетов по простому модулю р, причем хотя бы один из старших коэффициентов не делится па р, то эти многочлены взаимно просты над полем рациональных чисел. Ненулевой вычет, а называется квадратичным вычетом по модулю р, если уравнение х2 = а имеет решение в поле Z/(р). В противном случае вычет называется… Читать ещё >

Задачи. Дискретный анализ. Основы высшей алгебры (реферат, курсовая, диплом, контрольная)

3.1. Доказать, что минимальное подполе любого поля характеристики 0 изоморфно нолю рациональных чисел.
3.2. Доказать, что минимальное подполе любого поля характеристики р изоморфно полю GF (p).
3.3. Решить уравнение 4х = 1 в поле Z/(101).
3.4. Найти 73″¹ в поле Z/(103).
3.5. Решить систему уравнений

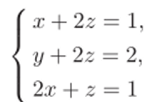
в поле вычетов по модулю 3 и по модулю 5.

3.6. Решить систему уравнений.

в поле вычетов по модулю 5 и по модулю 7.

3.7. Ненулевой вычет а называется квадратичным вычетом по модулю р, если уравнение х² = а имеет решение в поле Z/(р). В противном случае вычет называется квадратичным невычетом. Чего больше: квадратичных вычетов или квадратичных невычетов?

3.8. Доказать, что а является квадратичным вычетом по нечетному простому модулю р тогда и только тогда, когда.

_а(р—1)/2 _ 1 (_тос1р).

3.9. Найти произведение всех квадратичных вычетов по модулю 71.
3.10. Найти сумму всех квадратичных вычетов по модулю 67.

3.11. (Теорема Вильсона.) Доказать, что 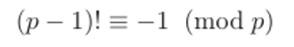Задачи. Дискретный анализ. Основы высшей алгебры. для простою р.

3.12. Доказать, что в поле GF (p) выполняются равенства:

3.13. Найти I²⁰⁰⁶ + 2²⁰⁰⁶ + З²⁰⁰⁶ + • • • 4−16²⁰⁰⁶ по модулю 17.
3.14. Сколько решений имеет уравнение х² = а в поле GF ( 2^П)?
3.15. Для каких из чисел п = 2,3,4,5,6, 7 существует поле из п элементов?
3.16. В поле F выполнено равенство 5 = 21. Верно ли, что в поле F выполнено равенство 7 = 15?
3.17. Можно ли в поле из 64 элементов найти подполе из 16 элементов?
3.18. Доказать, что поле из р² элементов, где р — простое число, имеет единственное собственное подполе.
3.19*. а) Доказать, что если многочлены f (x) и д (х) с целыми коэффициентами взаимно просты над полем вычетов по простому модулю р, причем хотя бы один из старших коэффициентов не делится па р, то эти многочлены взаимно просты над полем рациональных чисел.
б) Показать на примере, что для любого простого числа р обратное утверждение не верно.
3.20. Доказать, что многочлены f (x) и д (х) с целыми коэффициентами тогда и только тогда взаимно просты над полем рациональных чисел, когда они взаимно просты над полем

вычетов, но модулю р, где р любое простое число, исключая, быть может, конечное множество таких чисел.

3.21*. Доказать, что если многочлен f (x) с целыми коэффициентами приводим над полем рациональных чисел, то он приводим над полем вычетов по любому простому модулю р, не делящему старший коэффициент. Привести пример многочлена, приводимого над полем рациональных чисел, но неприводимого над полем вычетов, но модулю р, где р делит старший коэффициент.
3.22*. Существуют многочлены с целыми коэффициентами, неприводимые над полем рациональных чисел, но приводимые над полем вычетов по любому простому модулю р. Доказать, что таким будет, например, многочлен f (x) = х⁴ — 10т²+ 1. Это многочлен наименьшей степени с целыми коэффициентами, имеющий корень, а = /2 4- /3.
3.23. Многочлен f (x) = x²+ax+b, а, b € GF (5), неприводим над GF (5). Верно ли, что f (x) неприводим над GF (125)?
3.24. Доказать, что п делит

3.25. Решить уравнение х^р — х = 0 в поле GF (pⁿ).
3.26. Решить уравнение 5 т — 7 = 0 в поле из 169 элементов.
3.27. Решить уравнение х² + х 4- 4 = 0 в иоле GF (121).
3.28. Сколько решений имеет уравнение т²³ — х⁷ — 1 = 0 в поле GF (2⁴)?
3.29. Производная многочлена / ф 0 над полем характеристики р тождественно равна 0. Доказать, что этот многочлен приводимый.
3.30. Доказать, что многочлен / над полем F характеристики р, который взаимно прост со своей производной /', неприводим тогда и только тогда, когда уравнение х^р = х имеет в кольце F[x]/(f) ровно р решений.
3.31. Пусть (/,/') = 1 и v^p = v в кольце F[t]/(/), v? {0,1,…, р — 1}. (Здесь р — характеристика ноля коэффициентов F.) Доказать, что тогда для некоторого а € F многочлены v — а и / имеют нетривиальный общий делитель.
3.32. Доказать, что любая функция /: GF (pⁿ) —" GF (pⁿ) может быть представлена многочленом.
3.33. Является ли ж⁴ 4- 1 неприводимым многочленом над полем GF (3)?
3.34. Многочлен х⁵ + ж³+ж²4−1 разложить на неприводимые множители над полем вычетов по модулю 2.
3.35. Многочлен ж³ -I- 2ж² + 4ж + 1 разложить на неприводимые множители над полем вычетов по модулю 5.
3.36. Многочлен ж⁴ 4- ж³ 4- х4- 2 разложить на неприводимые множители над полем вычетов по модулю 3.
3.37. Многочлен ж⁴ 4- Зж³ + 2х² 4- ж + 4 разложить на неприводимые множители над полем вычетов, но модулю 5.
3.38. Разложить на неприводимые множители над полем вычетов по модулю 2 все нормированные многочлены второй степени от х.
3.39. Разложить на неприводимые множители над полем вычетов до модулю 2 все нормированные многочлены третьей степени от х.
3.40. Найти все нормированные многочлены второй степени от ж, неприводимые над нолем вычетов, но модулю 3.
3.41. Найти все нормированные многочлены третьей степени от ж, неприводимые над полем вычетов по модулю 3.
3.42. а) Проверить, что F = GF (7)[ж]/(ж² + ж — 1) является полем, б) Выразите обратный к 1 — ж в F в базисе 1, ж.
3.43. Найти порядок элемента ж + ж² в мультипликативной группе
а) поля GF (2)[ж]/(ж⁴ 4- ж 4−1);
б) поля GF (2)[ж]/(ж⁴ + ж³ + 1).
3.44. Найти количество неприводимых многочленов
а) степени 7 над полем GF (2);
б) степени 6 над полем GF (5);
в) степени 24 над полем GF (3).
3.45. Чему равно произведение всех ненулевых элементов поля GF (2⁶)?
3.46. Чему равна сумма всех элементов ноля GF (3')?
3.47. Многочлен / € GF (13)[t] седьмой степени разлагается над GF ( 13) на неприводимые множители степени 3 и 4. В каких полях GF (13″) многочлен / разлагается на линейные множители?
3.48. Найти наименьшее поле характеристики 2, в котором многочлен ж¹⁹ — 1 разлагается на линейные множители.
3.49. Построить изоморфизм между нолями

3.50. Доказать, что группа автоморфизмов ноля GF (pⁿ) циклическая, а ее порождающим является автоморфизм Фробениуса.
3.51. Конечная проективная плоскость порядка п — это такое семейство подмножеств L, …, L_m («прямых») конечного множества «точек» Р, что выполняются следующие свойства:
- • через каждую точку проходит п + 1 прямая;
- • каждая прямая содержит п + 1 точку;
- • через любые две различные точки проходит ровно одна прямая;
- • любые две различные прямые пересекаются ровно по одной точке.

Построить конечную проективную плоскость порядка q, где q — степень простого числа.

3.52. Пусть р — простое нечетное число. Определим для элемента а поля вычетов GF (p^rn) символ Лежандра. х (^а) как О, если а = 0, как +1, если уравнение х² = а имеет решение в поле GF (p^m), и как -1 в противном случае. Доказать
а) х (а)х (&) = х (аЬ)
б) еслир^т = 1 (mod 4), то х (^—1) = 1; если р^т = —1 (mod 4),

то х (—1) = -1;

в) E"_€gf (p-) х (в) = 0;
г) для любого Ь ф 0 выполнено S_a€GF (p" *) х («)х («+ Ь) = = -1.
3.53*. Матрица Адамара Н порядка п состоит из элементов ±1 и удовлетворяет условию

НН^Т = п1, где I — единичная матрица.

Построить матрицу Адамара порядка п = р^т + 1, где р — простое, а п делится на 4.

Показать весь текст

Заполнить форму текущей работой

Другие работы

Анализ развития отраслей экономики и социальной сферы региона

Крупнейшие предприятия нефтепереработки в Самарской области: Сызраньский нефтеперерабатывающий завод, Самарский нефтеперерабатывающий завод и Новокуйбышевский нефтехимический комплекс, в Республике Татарстан — нефтеперерабатывающий завод в Альтемевске; Волгоградский НПЗ — ведущий в стране по выработке смазочных масел. поволжье нефтегазохимический вода земля Очень высокого уровня достигли…

Реферат