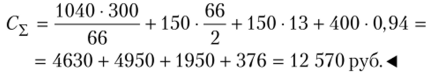Последовательность определения параметров стратегии с ФРЗ

Для формирования параметров модели ФРЗ необходимо знать следующие показатели:

• • постоянный (оптимальный) размер заказа ед.;
• • среднесуточный расход (интенсивность) Д ед/дн.;
• • время выполнения заказа т, дн.;
• • интервал времени контроля запаса Д, дн.

Величина Qo рассчитывается с помощью модели EOQ или на основании статистических данных. Рассмотрим последовательность определения параметров модели с ФРЗ.

Расчетными параметрами модели являются:

• • страховой запас, ед.;
• • максимальный запас, ед.;
• • уровень (точка) заказа, ед.;
• • средний уровень запаса, ед.;
• • общие затраты модели ФРЗ, руб.
• 1. Для расчета величины страхового (гарантийного) запаса может быть применена формула

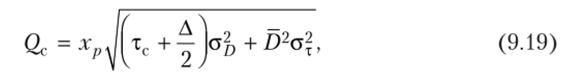
где т_с, а_х — среднее значение и среднее квадратическое отклонение времени выполнения заказа; Д o_D — среднее значение и среднее квадратическое отклонение среднесуточного расхода продукции.

2. Величина максимального запаса определяется по формуле.

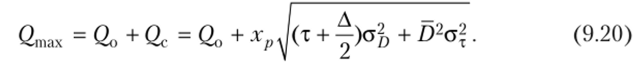
3. Уровень (точка) заказа Q_y3 может быть рассчитан по формуле.

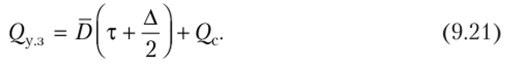
Если контроль осуществляется ежедневно (Д = 1 дн.), то составляющую 0,5А в формулах (9.19)—(9.21) можно не учитывать.

Таким образом, рассчитанные параметры позволяют построить «сетку» из опорных прямых (рис. 9.5) «объем заказа: Q_max, Q_y 3 Q<; время — интервал контроля А», на которую наносятся контрольные точки проверки состояния запаса и точки, характеризующие моменты заказа и его выполнения.

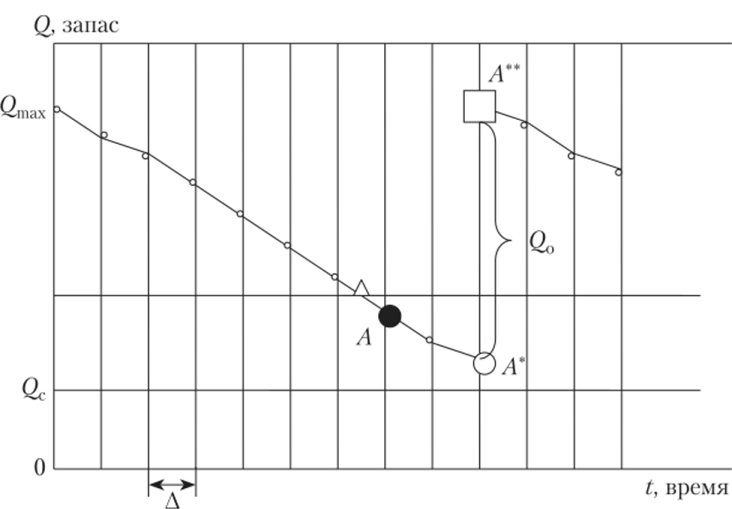
Рис. 9.5. Модель управления запасами с фиксированным размером заказа:

Л — точка пересечения уровня запаса (ROP); • — остаток запаса в момент заказа (Л); О — остаток запаса в момент поступления заказа (Л*);? — текущий запас в начале следующего интервала (Л**).

4. Средний уровень запаса определяется как.

5. Определим общие затраты модели с ФРЗ. Следует указать, что в литературе приведены различные варианты зависимости общих затрат для модели с ФРЗ, основное различие которых заключается в неоднозначной трактовке используемых обозначений и их аналитическом представлении, в частности с помощью табулированных функций или математического описания в виде интегралов.

Общие затраты могут быть определены по формуле.

где QJjCp а₍.) — страховой запас, рассчитываемый по формуле (9.19).

По аналогии с моделью ФПЗ, для определения оптимальных величин Q_<) и Qc, минимизирующих С-?, могут быть использованы численные (итерационные) и аналитические способы. В частности, известен подход^[1], согласно которому для вычисления Q, и Q_c используется система двух уравнений дСу ‘ дСу

= 0 и —= 0.

3Q эа При использовании итерационной процедуры алгоритм вычисления Q, и включает^[2]:

• 1. Расчет, но формуле Харриса — Уилсона.
• 2. Оценку величины

где Р — вероятность отсутствия дефицита.

• 3. Определение х_р с использованием таблицы прил. 1 для нормального закона распределения.
• 4. Определение 1(х_р) по таблице прил. 1.
• 5. Расчет откорректированной величины оптимальной партии заказа

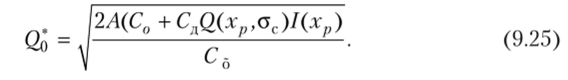
• 6. Повторение процедуры вычисления до достижения заданной точности.
• ? Разбор ситуации

Для данных, рассмотренных в предыдущих ситуациях гл. 9, изменим условие — заказы будут выполняться по стратегии с фиксированным размером, а также добавим недостающие данные. Напомним, какая исходная информация уже известна: А = 1040 ед., С₀ = 300 руб., С_х = 150 руб/ед. • год, С_л= 400 руб/ед. • год, I) = 4 ед/дн.; а_п= 1 ед/дн.

Допустим, что время выполнения заказа подчиняется нормальному закону с параметрами: среднее значение т_с= 6 дн., о_т = 1,5 дн. Определим основные параметры (величина заказа Q, страхового запаса Q. и др.) для стратегии с фиксированным размером заказа.

• 1. На первом этапе определим оптимальную партию поставки по формуле Харриса — Уилсона, она равна Q, = 64,5 ед.
• 2. На втором этапе рассчитаем вероятность отсутствия дефицита по (9.24):

• 3. Для определения коэффициента х_р воспользз’емся таблицей прил. 1: х_р = 2,0.
• 4. Для оценки интеграла потерь 1(х_р) воспользз’емся таблицей прил. 1: 1(х_р) = 0,0085.
• 5. Рассчитаем величину среднего квадратического отклонения страхового запаса по (9.19) при условии, что интервал времени контроля запаса Д ~ 0:

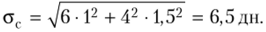
6. Рассчитаем величину откорректированной партии заказа по (9.25):

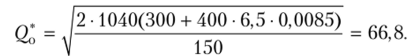
7. Согласно алгоритму, повторим расчет Р при Q,* = 66,8 и определим вероятность отсутствия дефицита.

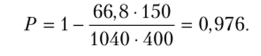
• 8. Находим х_р = 1,97 и 1(х_р) = 0,092; соответственно, Q] = 66,4 ед. Принимаем, что значение Q,_)IIT ~ 66 ед.
• 9. Рассчитаем:
  • • страховой запас, но (9.19):

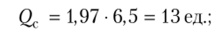
• максимальный запас по (9.20):

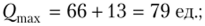
• ROR

• величину дефицита 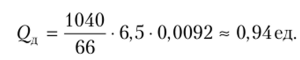Примем <2_Л = 1 ед.

10. Рассчитаем общие затраты по (9.23):

• [1] Букан Дж. у Кенигсберг Э. Научное управление запасами. М.: Наука, 1967; Хедли Дж., Уайтин Т. Анализ систем управления запасами. М.: Наука, 1969.
• [2] Ballou R. Н. Business Logistics Management. 3rd ed. Upper Saddle River, N. Y.: PrenticeHall. Inc, 1992.