Перспективность членов функционального уравнения

Существенного сокращения числа членов оптимальных последовательностей в методе динамического программирования можно добиться на основе расчета для них оптимистических оценок. Если окажется, что для какоголибо члена функционального уравнения оптимистическая оценка окажется хуже известного допустимого решения, то такой член из дальнейшего рассмотрения может быть исключен. Это позволяет уменьшить емкостную сложность алгоритма динамического программирования.

Для рассматриваемой нами задачи верхняя граница для членов оптимальных последовательностей может быть рассчитана по формуле.

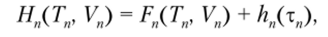
п N.

где F_n(T_n, V_a) = max? wXxj); h_n(x_n) = max I wXx) j-i

при ограничении.

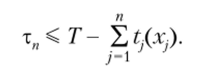
Расчет второго слагаемого верхней границы можно рассматривать как решение вспомогательной задачи, которое может быть осуществлено точно или приближенно с нарушением условия целочисленное™ (дискретности).

Для иллюстрации метода предположим, что у нас имеется приближенное решение основной задачи со значением целевой функции: W₀ = 53; Х₀ = = (x_{ = 1, х₂= 2,х₃= 1, х_А = 2).

При /? = 2 членами оптимальной последовательности F₂(T₂, V₂) для нашей задачи являются:

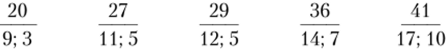
Для этих членов вспомогательная задача может быть решена на основе следующих данных (табл. 11.3.19).

Данные для оценки перспективности членов уравнения F₂{T₂, V₂)

В табл. 11.3.19 величина hj (x) показывает приоритет перехода от одного решения с наименьшими значениями ??(*.) к другим решениям с большими значениями tj (Xj). При этом.

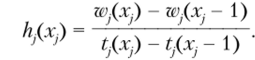
Улучшение решения проводится по условию.

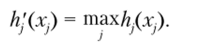
Результаты оценки перспективности F₂(T₂, V₂) приведены в табл. 11.3.20. Из нее очевидно, что дальнейшим исследованиям целесообразно подвергать только третий и четвертый члены, у которых верхняя граница решения Я₂(Г₂, V₂) = 55 >W₀ = 53.

При п = 3 перспективными оказались первый и второй члены. Результаты решения приведены в табл. 11.3.21.

Таблица 11.3.20

Оценка перспективности членов функционального уравнения.

Таблица 11.3.21

Определение членов функционального уравнения F₃(T_V V₃) при п = 3.

На четвертом этапе получаем оптимальное значение целевой функции W* = 55 (см. табл. 11.3.22)/.

Таблица 113.22

Определение членов функционального уравнения F_A(T_Af V_A) при п- 4.

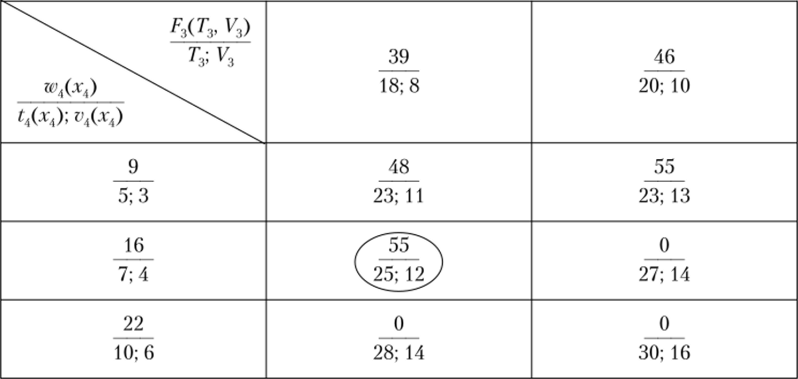
Как видим, табличный способ решения функционального уравнения после исключения бесперспективных членов оказался значительно короче стандартной процедуры динамического программирования.

Рассмотренные выше алгоритмы ресурсно-временной оптимизации проектов базировались на использовании метода динамического программирования. Возможности метода при сетевой интерпретации процедуры поиска оптимального решения ограничиваются обозримостью представления допустимых вариантов. Табличное представление хода решения обладает лучшей наглядностью и, в свою очередь, демонстрирует проблему «размерности» в динамическом программировании.

Возможность снижения сложности метода динамического программирования может быть достигнута за счет эквивалентных преобразований исходных данных и на основе свертки оптимальных последовательностей рекуррентных соотношений решаемой задачи^[1].

Достаточно эффективным приемом снижения емкостной и временной сложности комбинаторных алгоритмов является вычисление оптимистической оценки перспективности для рассматриваемых вариантов решений на основе комплексного использования метода динамического программирования и метода ветвей и границ^[2].

Развитием детерминированных подходов к ресурсно-временной оптимизации является вероятностный экспресс-анализ проектов^[3].

• [1] Бабаев А. А., Огнев В. Н. Свертка членов функционального уравнения при оптимизациипоказателя надежности // Надежность и контроль качества. 1979. № 6. С. 3—9.
• [2] Алексеев О. Г., Бабаев А. А. Комбинированный метод оптимального распределения массивов по уровням памяти ЭВМ // Механизация и автоматизация управления. 1978. № 2.С. 14−17/
• [3] 1 Ботвин Г. А. и др. Модели и методы экспресс-анализа инвестиционных проектов. СПб. :Изд-во Политехи, ун-та, 2009.