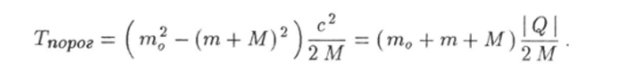Столкновения релятивистских частиц

Соударения элементарных частиц и атомных ядер, которые могут двигаться со скоростями, близкими к скорости света, подчиняются законам сохранения импульса и энергии. Получим уравнения, выражающие эти законы, при помощи обобщенного принципа относительности, согласно которому они должны быть ковариантны. Таковыми могут быть только тензорные уравнения. В рассматриваемом случае уравнения, выражающие собой законы сохранения импульса и энергии сталкивающихся частиц, должны иметь вид.

где р^ - 4-импульсы соударяющихся частиц, i = 1, 2, п — номера этих частиц, п — их число; р^ - 4-импульсы частиц после столкновения, к = п + 1, …, п + п' - номера этих частиц, п' - их число; р = 1, 2, 3, 4. Обе части равенства (10.83) есть 4-векторы. Поэтому преобразования Лоренца не изменяют вид этого равенства, т. е. в любой инерциальной системе отсчета сумма импульсов р^ частиц до столкновения равна сумме (*).

импульсов р_и частиц после их столкновения.

Формулы (10.77) дают возможность записать уравнения (10.83) следующим образом:

где pi, Е{ и pi, Е_к — релятивистские импульсы и энергии частиц до и после столкновения соответственно. Уравнения (10.84) и (10.85) выражают собой законы сохранены импульса и энергии системы сталкивающихся частиц.

Согласно формуле (10.20) анергия Е частицы массы т равна сумме энергии покоя тс² и кинетической энергии Т :

При помощи этого соотношения запишем закон сохранения энергии (10.85) так: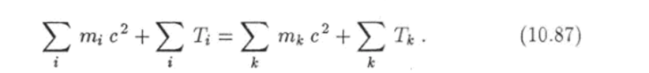

Энергией реакции Q называют разность кинетических энергий частицпродуктов реакции и исходных частиц:

Используя это определение, придадим уравнению (10.87) следующий вид:

где энергия реакции определяется разностью

масс частиц до и после реакции.

Анализируя полученные формулы, приходим к выводу, что в том случае, когда суммарная масса частиц, вступающих в реакцию, больше массы ее продуктов (Ат > 0), энергия реакции Q положительна. При этом, как видно из равенства (10.88), кинетическая энергия продуктов реакции больше, чем кинетическая энергия исходных частиц:

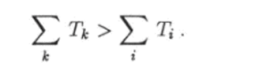
В таком случае говорят, что реакция протекает с выделением тепла. При этом часть Q энергии покоя исходных частиц переходит в кинетическую энергию продуктов реакции. На этом факте основан принцип работы реакторов атомных электростанций.

" Горючим" веществом в атомных реакторах является уран 92U²³⁵ или плутоний. Числа 92 (порядковый номер урана в таблице Менделеева или зарядовое число) и 235 (массовое число) означают, что ядро урана состоит из 92 протонов и 235 — 92 = 143 нейтронов. При захвате медленного нейтрона п ядро урана-235 превращается в изотоп с массовым числом.

236:

который нестабилен и распадается различными путями на составные части. Одна из реакций деления урана-236 выглядит так:

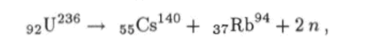
т.е. ядро урана-236 распадается на ядро цезия Се, ядро рубидия Rb и два нейтрона. При этом сумма масс ядра урана-235 и нейтрона превосходит суммарную массу частиц-продуктов реакции деления, которые называются осколками деления. Энергия реакции (10.90), соответствующая избытку массы Ат, превращается в кинетическую энергию осколков деления и энергию возникающего в процессе реакции электромагнитного излучения.

Рассмотрим несколько примеров применения законов сохранения импульса (10.84) и энергии (10.85).

Так как энергия релятивистской частицы больше или равна ее энергии покоя, энергии Е и Е% осколков деления таковы, что Пример 1. Распад частицы. Пусть частица массы М самопроизвольно делится на два осколка с массами mi и т₂. Такой процесс удобно изучать в системе центра инерции, т. е. в системе, относительно которой частица М до распада покоилась. Уравнения (10.84) и (10.85) в таком случае будут иметь вид.

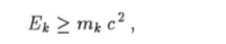
где к = 1, 2. В силу этих неравенств уравнение (10.93) имеет смысл только при условии, что масса А/ больше суммы масс осколков:

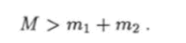
Только при этом условии возможен самопроизвольный распад частицы. В противном случае частица будет стабильной, т. е. неподверженной самопроизвольному распаду.

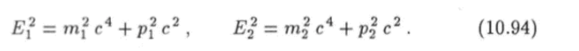
Уравнения (10.92) и (10.93) следует дополнить соотношениями, связывающими импульсы и энергии осколков деления. Согласно (10.78) можно записать Из закона сохранения импульса (10.92) следует, что модули импульсов Pi и р₂ осколков деления одинаковы:

Вычтем первое уравнение (10.94) из второго. С учетом равенства (10.95) получим: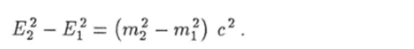

Это уравнение вместе с уравнением (10.93) образует систему с двумя неизвестными Е и .?₂, которая имеет следующее решение:

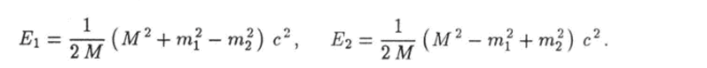aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Пример 2. Упругое столкновение двух частиц. Пусть частица массы т налетает на покоящуюся частицу массы М. Законы сохранения импульса и энергии для упругого столкновения этих частиц выражаются уравнениями где р, Е и pi, Ei — импульсы и энергии налетающей частицы соответственно до и после столкновения, р₂ и ?₂ — импульс и энергия частицы М после столкновения. Причем импульсы и энергии частиц связаны соотношениями.

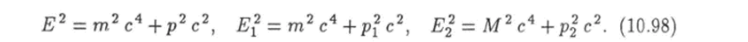
Из уравнения (10.96) найдем, что 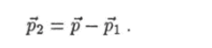Возведя это равенство в квадрат, получим:

где в — угол рассеяния налетающей частицы, т. е. угол между векторами р и pi (рис. 10.11).

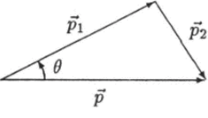
Рис. 10.11.

К закону сохранения импульса

Если величины р_} Е и в считать заданными, то импульсы pi, рг и энергии Ei, Е₂ частиц после столкновения можно найти из уравнений (10.97) — (10.99).

Пример 3. Неупругое столкновение частиц. Рассмотрим случай, когда релятивистская частица с массой покоя т при столкновении с покоящейся частицей массы М возбуждает реакцию, в результате которой рождаются новые частицы с массами mi, т_2у … такими, что.

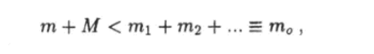
где т₀ - сумма масс рождающихся частиц. При этом сумма энергий покоя сталкивающихся частиц будет меньше суммарной энергии покоя рождающихся частиц, а энергия реакции.

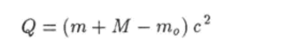
будет отрицательной (Q < 0).

Уравнение (10.89) в рассматриваемом случае принимает вид.

где Т — кинетическая энергия налетающей частицы тп. Как видно из этого уравнения, если Q < 0, то реакция может осуществиться только при условии, что кинетическая энергия Т налетающей частицы ш превышает некоторое пороговое значение: Т > Тпорог- В противном случае дело ограничится упругим соударением частиц. Найдем пороговую энергию реакции. Для этого запишем законы сохранения импульса и энергии:

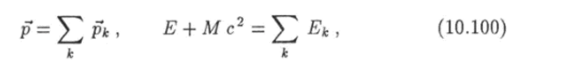
гдерн Е — импульс и энергия налетающей частицы т, р* и Ек — импульс и энергия одной из родившихся частиц, к =1, 2, … ;

Когда кинетическая энергия Т налетающей частицы равна пороговому значению, этой энергии хватает только на то, чтобы реакция произошла, но ее недостаточно для того, чтобы образовавшиеся частицы разлетелись в разные стороны. Иначе говоря, в этом случае все образовавшиеся частицы будут иметь одну и ту же скорость v. При этом их импульсы и энергии будут.

Подстановка этих выражений в равенства (10.100) дает.

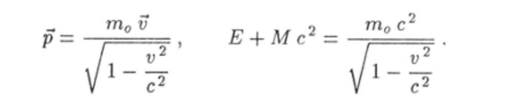
Правые части этих равенств удовлетворяют соотношению типа (10.101). Поэтому их левые части таковы, что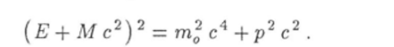

Это уравнение вместе с уравнением (10.101) образует систему с двумя неизвестными Е и р. Исключив импульс р путем вычитания одного уравнения из другого, получим:

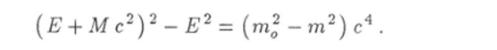
Решение этого уравнения имеет вид.

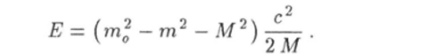
Теперь найдем пороговое значение кинетической энергии. Согласно определению (10.86)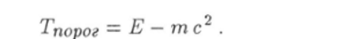

После несложных преобразований будем иметь.