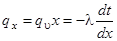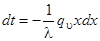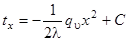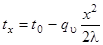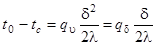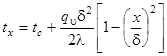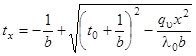Теплопроводность тел с внутренними источниками теплоты

На практике могут встретиться случаи, когда теплота возникает внутри объема тела за счет внутренних источников, например за счет прохождения электрического тока, химических реакций, ядерного распада и т. п. Поскольку объемное тепловыделение может быть не только равномерным, но и неравномерным, для таких процессов важным является понятие мощности внутренних источников теплоты. Эта величина, обозначаемая q_v, определяет собой количество теплоты, выделяемое единицей объема тела в единицу времени, она измеряется в Вт/м³. При поглощении теплоты внутри объема тела, например при эндотермической реакции, величина q_v отрицательна; она характеризует интенсивность объемного стока теплоты.

При наличии внутренних источников (стоков) теплоты основной задачей является расчет температурного поля внутри тела.

Теплопроводность плоской стенки

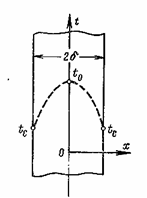
Рассмотрим однородную плоскую стенку толщиной 2д, коэффициент теплопроводности л которой постоянен. Внутри этой стенки имеются равномерно распределенные источники теплоты q_v. Выделившаяся теплота через боковые поверхности стенки передается в окружающую среду. Относительно площади стенки в среднем сечении процесс теплопроводности будет протекать симметрично, поэтому именно здесь целесообразно поместить начало координат, а ось х направить перпендикулярно боковым поверхностям (рис. 7).

Рисунок 7 — Теплопроводность с внутренними источниками теплоты в трубе.

Из уравнения теплового баланса следует, что при наличии внутренних источников теплоты плотность теплового потока в плоской стенке линейно возрастает с увеличением х и равна.

(56).

Из этого уравнения видно, что при х =0 q = 0, а при х = д q_д = q_v д, т. е. достигает своего максимального значения. Согласно закону Фурье.

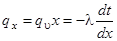
(57).

Произведя разделение переменных, имеем.

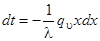
(58).

Интегрируя это уравнение, получаем.

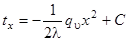
(59).

Постоянная интегрирования С определяется из граничных условий. При х = 0 t = t₀ = С, и уравнение изменения температуры принимает вид.

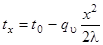
(60).

При х = д, t = t_c; в этом случае из уравнения (59) следует.

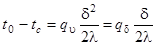
(61).

Здесь разность t₀ — t_c означает перепад температуры между серединой и внешними поверхностями плоской стенки, а q_д = q_лд — плотность теплового потока на этих граничных поверхностях (при х = д).

Если температура t₀ неизвестна, то значение постоянной С можно выразить через t_c и уравнение температурной кривой в этом случае, принимает вид.

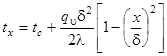
(62).

Приведенные выводы показывают, что при наличии равномерно распределенных внутренних источников теплоты распределение температур в плоской стенке носит параболический характер. Наибольшее значение температура имеет в средней плоскости (х = 0).

При больших перепадах температуры необходимо учитывать зависимость коэффициента теплопроводности от температуры,. При х = 0 и . Подставляя значение С в уравнение (62) и решая последнее относительно t, получаем следующее уравнение температурной кривой.

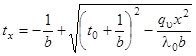
(63).