Расчет параметров элементов схемы замещения

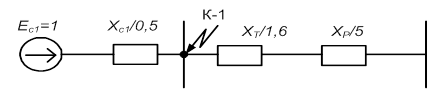
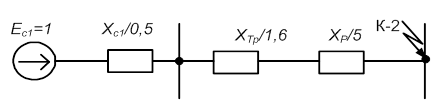
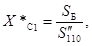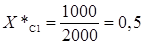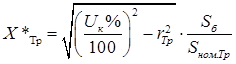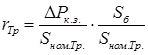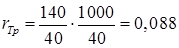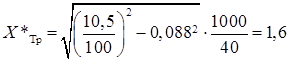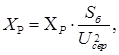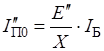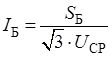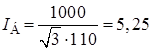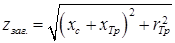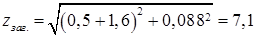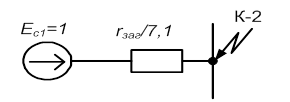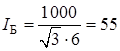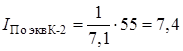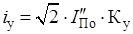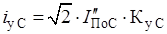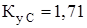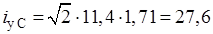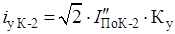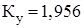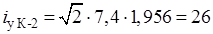Определяем опоры элементов схемы замещения (Рисунок 3.2) по формулам приближенного приведения. Расчет ведем в относительных единицах.

Произвольно задаемся базисной мощностью, МВА.

.

Сопротивление системы 110 кВ.

(2.1).

где — сверхпереходная мощность к.з. системы 110 кВ (из задания на проектирование), МВА.

.

Сопротивление трансформаторов.

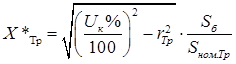
(2.2).

где — напряжение к.з. трансформатора %;

— номинальная мощность трансформатора, МВА;

— реактивное сопротивление трансформатора.

Реактивное сопротивление трансформатора.

.

Сопротивление трансформаторов.

Сопротивление реакторов.

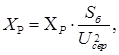
(2.3).

где — сопротивление реактора, зависит от матеріла проводніка;

— базисная мощность, МВА;

— напряжение на которой работает напряжение, кВ.

.

Расчет токов короткого замыкания на напряжении 110 кВ

Для расчета токов короткого замыкания, строим схему замещения относительно точки К-1 (Рисунок 2.2). Учитываются те элементы, которые непосредственно влияют на к.з. Поскольку весь дальнейший расчет ведется в относительных единицах, то для упрощения записи опустим значок *.

Рисунок 2.3 — Превращение схемы замещения относительно точки К-1.

Рисунок 2.4 — Окончательно преобразованная схема замещения относительно точки К-1.

Начальное действующее значение периодической составляющей тока к.з., кА.

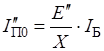
(2.4).

где — базисный ток, кА.

Базисный ток, кА.

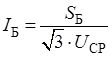
(2.5).

где — среднее напряжение степени, на которой состоялось к.з., кВ.

.

Начальное действующее значение периодической составляющей тока к.з. на степени 110кВ в разных ветках, кА.

.

Расчет токов короткого замыкания на напряжении 6 кВ

Используя расчет тока к.з. для точки К-1, имеем:

Рисунок 2.5 — Схема замещения относительно точки К-2.

Общее сопротивление системы и трансформатора.

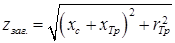
(2.6).

Рисунок 2.6 — Окончательно преобразованная схема замещения относительно точки К-2.

Базисный ток, кА.

.

Начальное действующее значение периодической составляющей тока к.з. на степени 6кВ в одной ветке, кА.

.

Ударный ток, кА.

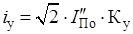
(2.7).

где — ударный коэффициент.

Ударный ток к.з. на шинах РУ 110 кВ для разных составляющих находим по выражениям, кА Система К-1.

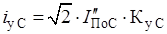
(2.8).

где [4, табл. 3.8].

.

Ударный ток к.з. на системах шинах 6 кВ, кА.

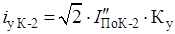
(2.9).

где [1, табл. 3.8].

.

Результаты расчетов токов к.з. возводим в таблицу 2.1.

Таблица 2.1 — Токи короткого замыкания.