Представление модулированных сигналов амплитудно-фазовыми диаграммами

Удобным представлением модулированного сигнала является амплитудно-фазовая диаграмма (сигнальная конструкция — signal structure; сигнальное созвездие — signal constellation), представляемая в полярной системе координат. Строят амплитудно-фазовую диаграмму следующим образом (рис. 2.55). Пусть имеются временные диаграммы импульсов с несущим колебанием, отражающие единичный е, = eft) = cos (co₍/: +ср₀) и нулевой е₂= e₂(t) = 0 передаваемые двоичные символы (рис. 2.55, а, б). Отложим по горизонтальной оси диаграммы фазу (от 0 до 360°), а по вертикальной — амплитуду передаваемого сигнала. Теперь для каждого двоичного сигнала есть два параметра — амплитуда и фаза, т. е. две координаты. Значит, всю информацию о сигналах е, и е₂ можно отобразить соответствующими векторами (один из которых с пулевой амплитудой) на комплексной плоскости — вещественная и мнимая оси обозначены соответственно как Re и 1ш (рис. 2.55, в).

Из геометрии известно, что при вращении комплексного вектора с частотой исследуемого колебания его проекция на действительную ось дает вещественный сигнал. Для упрощения диаграммы, особенно при отображении сигналов современных миогоиозициониых видов модуляции, обычно изображают только конечные точки векторов, исходящих из начала координат, а сами векторы, как правило, опускают. В этом случае можно перейти к диаграмме, на которой два колебания вместо векторов представлены.

Рис. 2.55. К построению амплитудно-фазовой диаграммы сигналов:

а, б — временные диаграммы; в — векторные диаграммы; г — сигнальные точки точками е_{ и е₂ (рис. 2.55, г). Часто опускают и сами оси Re и Im, подразумевая, что они проходят через центр симметрии фигуры. Такую картинку называют точечной амплитудно-фазовой диаграммой модулированных сигналов. По существу эти точки представляются комплексными числами. Каждая точка называется сигнальной. Совокупность сигнальных точек передаваемых символов и образует амплитудно-фазовую диаграмму, или сигнальное созвездие. Форма созвездия соответствует виду модуляции, а расстояния между точками характеризуют помехоустойчивость.

Не вдаваясь особенно в подробности, скажем, что помехоустойчивость тем выше, чем больше расстояние d между ближайшими точками созвездия на комплексной плоскости. На практике используют созвездия, содержащие от четырех до нескольких тысяч точек. Такой способ является очень удобным при представлении и более сложных модулированных колебаний (рис. 2.56). Квадратурно-модулированное колебание, изображенное на рис. 2.49, д, представлено с помощью амплитудно-фазовой диаграммы в векторной форме на рис. 2.56, а. Как очевидно, пространство комплексной плоскости используется не слишком эффективно — занят только один квадрант. На рис. 2.56, б показана КАМ с четырьмя одинаковыми фазовыми сдвигами в 90° (КАМ-4; (ММ-4), вектор которой при модуляции двух квадратурных компонентов занимает также четыре точки, но уже в четырех квадрантах, что повышает помехоустойчивость системы модуляции.

Рис. 2.56. Расположение сигнальных точек на амплитудно-фазовых диаграммах:

а — в квадратурной ЦФМ; 6 — в 4-позиционной ЦФМ; в — временные диаграммы сигналов, соответствующих четырем положениям вектора 4-ЦФМ Временные диаграммы сигналов, соответствующих этим положениям вектора, показаны на рис. 2.56, в. Амплитуды сигналов равны, поэтому модуляцию называют четырехпозиционной цифровой фазовой модуляцией (КФМ-4 — квадратурным КФМ-сигналом) — это и есть упоминаемая QPSK. Поскольку в каждом канале осуществляется амплитудная манипуляция, этот вид модуляции называют также QASK.

Скажем еще несколько слов о помехоустойчивости систем цифровой модуляции.

В частности, отметим, что за счет использования двумерного характера гармонического несущего колебания квадратурная манипуляция обеспечивает большую помехоустойчивость (т.е. меньшую вероятность ошибки приема символа), чем АМн и ФМн. Как уже указывалось, помехоустойчивость модулированных сигналов тем выше, чем больше расстояние d между ближайшими точками созвездия на комплексной плоскости. Сравним для примера помехоустойчивости 16-иозиционных амплитудной, фазовой и квадратурной манипуляций (рис. 2.57). На практике применяют различные многопозиционные системы ЦФМ (они относятся к системам с нелинейной модуляцией; системы сигналов с амплитудной модуляцией считают линейными).

Для повышения качества передачи сообщений (что называют минимизацией средней вероятности ошибочного приема в канале связи с шумом) надо подбирать сигнальные последовательности, у которых сигнальные точки разрешенных кодовых комбинаций находятся друг от друга на максимально возможном расстоянии.

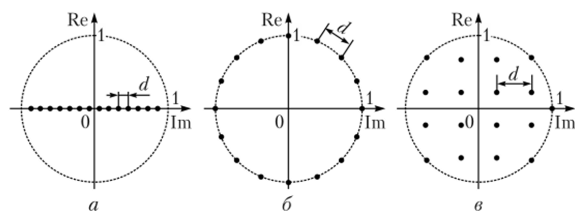
Рис. 2.57. Сравнение помехоустойчивости разных 16-нозиционных манипуляций:

а — амплитудной; б — фазовой; в — квадратурной Задача согласования модулированного сигнала с радиоканалом решается оптимизацией формы и числа точек двумерного сигнального созвездия. В частности, сигнал QAM, переносящий п бит/символ, т. е. имеющий 2п точек сигнального созвездия, обладает следующим интересным свойством. Если п — целое четное число, то сигнальное созвездие представляет собой простое отображение двух независимых квадратурных каналов и обладает квадратной формой, а точки созвездия имеют координаты в виде нечетных чисел. Если п — число целое нечетное, то созвездие имеет крестообразную форму при расположении точек в узлах той же прямоугольной координатной сетки, что и для четного п. Минимальное относительное расстояние между любыми двумя точками созвездия равно двум. При увеличении порядка созвездия (числа бит на символ) на единицу надо повышать мощность передатчика на 3 дБ (в два раза).

Сигнально-кодовые конструкции (треллис-модуляция). Многопозиционные сигналы с так называемой плотной упаковкой (например, АФМ, КАМ, ЦФМ и др.) обеспечивают высокую удельную скорость передачи информации за счет снижения помехоустойчивости. В то же время применение помехоустойчивого решетчатого кодирования может повысить помехоустойчивость при определенном снижении удельной скорости. Каждый из этих способов дает выигрыш по одному показателю в обмен на ухудшение другого. Но важным является одновременное повышение как помехоустойчивости, так и скорости передачи информации. Решение этой задачи возможно при использовании ансамблей многопозиционных сигналов совместно с помехоустойчивым кодированием. Очевидно, что при этом необходимо сформировать такие сигнальные последовательности, точки которых в многомерном пространстве плотно упакованы (для уменьшения отношения сигнал/шум, а значит, создания высокой частотной эффективности) и достаточно разнесены (чтобы обеспечить высокую энергетическую эффективность). Такие сигнальные последовательности, построенные на базе многопозиционных сигналов и помехоустойчивых кодов, называют сигнально-кодовыми конструкциями (СКК; signal code structure — SCS; в иностранной литературе СКК носят название треллис-модуляции; trellis coded modulation — ТС AT).

Выбранная комбинация многопозиционного сигнала и помехоустойчивого кода позволяет повысить помехозащищенность передачи информации наряду со снижением требований к отношению сигнал/шум в канале на 3— 6 дБ. При этом число сигнальных точек увеличивается вдвое за счет добавления к информационным битам одного избыточного, образованного путем сверточного кодирования. Расширенный таким образом блок битов подвергается все той же КАМ.

В процессе демодуляции производится декодирование принятого сигнала с шумами по алгоритму Витерби (см. далее). Именно этот алгоритм за счет использования введенной избыточности и знания предыстории процесса приема сообщения позволяет по критерию максимального правдоподобия выбрать из сигнального пространства наиболее достоверную эталонную точку.

В качестве помехоустойчивых кодов в системах СКК используют сверточные и каскадные коды, а многопозиционных сигналов — сигналы ФМ, АФМ и ЧМЫФ.

Сейчас распространены следующие виды импульсной и цифровой модуляции:

• • в спутниковой связи — QPSK, 16(ММ, BPSK (binary phase-shift keying — бинарная фазовая манипуляция — скачкообразное переключение фазы синусоидального сигнала на к при неизменной амплитуде, при этом фазе О ставится в соответствие логический нуль, а фазе п — логическая единица);
• • в радиорелейных линиях связи — BPSK, QPSK, 8PSK, 16(ММ, 32(ММ, 64(ММ, 128(ММ, 256Q4M;
• • в кабельных линиях связи — QPSK, 16(ММ, 64Q4M, 256Q4M;
• • в радиотелефонии систем сотовой связи — от 16(ММ до 16384(ММ.