Элементы прогнозирования и интерполяции

Анализ динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования — определения будущих размеров уровня экономического явления.

Процесс прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, т. е. прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой, и в прошлое — ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию. Первоначальные прогнозы, как правило, сводятся к экстраполяции тенденции. При этом могут использоваться разные методы в зависимости от исходной информации. Можно выделить следующие элементарные методы экстраполяции: на основе среднего абсолютного прироста, среднего темпа роста и на основе применения метода наименьших квадратов и представления развития явлений во времени в виде уравнения тренда, т. е. математической функции уровней ряда (у) от фактора времени (t).

Прогнозирование по среднему абсолютному приросту

может быть выполнено в том случае, если общая тенденция считается линейной, т. е. метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).

В этом случае, чтобы получить прогноз на / шагов вперед (г — период упреждения), достаточно воспользоваться следующей формулой:

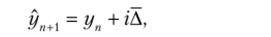
где у_п+1 — прогнозная оценка значения (п + 1)-го уровня ряда; у_п — фактическое значение в последней п-й точке ряда (конечный уровень ряда); Д — значение среднего абсолютного прироста, рассчитанное для ряда динамики y_v y_v …, у_п.

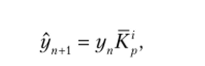
Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения прогнозного значения на i шагов вперед необходимо использовать следующую формулу:

где К_р — средний коэффициент роста, рассчитанный для рядаy_vy_v …, у_п.

К недостаткам рассмотренных методов следует отнести то, что они учитывают лишь конечный и начальный уровень ряда, исключая влияние промежуточных уровней. Тем не менее методы среднего абсолютного прироста и среднего темпа роста имеют весьма широкую область применения, что объясняется простотой их вычисления. Они могут быть использованы как приближенные, простейшие способы прогнозирования, предшествующие более глубокому количественно-качественному анализу.

Наиболее распространенным методом прогнозирования является аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (7).

При таком подходе к прогнозированию предполагается, что размер уровня, характеризирующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени. На практике для описания тенденции развития явления широко используются модели кривых роста, представляющие собой различные функции времени у

Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы:

• 1) выбор одной или нескольких кривых, форма которых соответствует характеру изменения ряда динамики;
• 2) оценка параметров выбранных кривых;
• 3) проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой роста;
• 4) расчет точечного и интервального прогнозов.

Остановимся на величине доверительного интервала прогноза, который определяют по формуле.

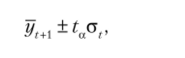
где у_[Л — расчетное значение уровня; t_a — доверительная величина, определяемая на основе 7-критерия Стыодента; а — средняя квадратическая ошибка тренда.

Вместо 7-критерия удобно использовать коэффициент.

(К*).

Например, необходимо провести прогноз на 2011 — 2012 гг. по данным о количестве проданных квартир в регионе N (см. табл. 8.5).

Для экстраполяции используем уравнение тренда, полученное по прямой y_t =39,7 + 0,257. Подставив соответствующее значение 7 в наше уравнение, получим точечные прогнозы на 2011—2012 гг. (графа 2 табл. 8.9). Для построения интервальных прогнозов рассчитаем среднеквадратическую ошибку тренда (ст_г = 0,56) и используем значения Ю.

Результаты прогноза представлены в табл. 8.9.

¹ Четыркин Е. М. Статистические методы прогнозирования. М.: Статистика, 1975. С. 183.

Таблица 8.9

Прогнозные значения численности проданных квартир в регионе N на 2011—2012 гг.

При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, т. е. к интерполяции.

Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста, а также с помощью аналитического выравнивания. При интерполяции предполагается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого неизвестны.