Примеры расчетов прогнозирования

Ключевые понятия и определения

Вероятности заданного числа событий. Вероятность выигрыша в лотерею. Расчет необходимого числа попыток.

Теория вероятностей утверждает, что случайные события, те, которые мы стремимся предсказать, могут происходить довольно часто. Можно провести такой опыт. Если на вашем предприятии мужчин и женщин примерно поровну, попытайтесь предугадать, кто сейчас первым войдет в помещение: «он» или «она». Сказав «он», вы рискуете ошибиться лишь в половине всех случаев — около 50% ваших предсказаний обязательно оправдается.

Зато, если вы рискнете предсказать, что оба вошедших подряд окажутся мужчинами, вероятность резко упадет и окажется равной всего 25% (по теореме умножения 0,5×0,5). Ваше предсказание сбудется лишь в одном случае из четырех. Нет, таким путем в прорицатели не выбиться.

Существует, однако, нехитрый способ добиться значительного увеличения числа «вещих» предсказаний. Для этого нужно только загадать «кто войдет» несколько по-иному: если вы будете утверждать, что мужчин окажется не менее, чем один из нескольких вошедших подряд, то это вайю предсказание имеет значительно больше шансов на успех. Расчет, сделанный по правилам теории вероятностей, показывает, что вероятность увидеть хотя бы одного мужчину из пяти вошедших равна 93%. Делая такое предсказание, вы практически ничем не рискуете — оно сбудется наверняка.

С высокой точностью сбудется также и предсказание прихода не менее двух мужчин (или, если хотите, женщин — это в подобных задачах не имеет значения) из пяти вошедших. Вероятность этого события равна 81%, т. е. она тоже высока. И даже предсказывая, что из пяти человек не менее трех окажется лицами названного вами пола, вы все еще сохраните шансы простыть пророком — вероятность 50%.

Приведем для разных случаев маленькую, но полезную таблицу 7.1, взятую из теории вероятностей.

Таблица 7.1.

Вероятности прихода предсказанного количества мужчин или женщин, %.

Посмотрев таблицу, вы можете уверенно предсказать, например, что из пяти вошедших будет не менее двух мужчин (или женщин). Вероятность этого события очень большая — 81%. В восьми случаях из десяти ваше предсказание сбудется.

Сказанное приоткрывает некоторые профессиональные тайны прорицательниц и гадалок.

Предположим, гадалка предсказывает пять каких-то событий, которые могут равно как произойти, так и не произойти — точно так же, как в одинаковой степени могут войти мужчина и женщина. Такими предсказаниями могут быть, например, «приятная встреча», «лихой недруг», «дальняя дорога», «получение известия», «нечаянная радость» ит. п.

Вероятность того, что сбудутся все пять предсказаний, как показывает расчет, исключительно мала — всего 3,1%. Но легковерному человеку вполне достаточно, если состоится хотя бы не менее двух-трех из них. Заметьте, не менее — это может быть и два, и три, и четыре, и даже пять. А такое количество пророчеств, мы уже знаем, происходит с высокой вероятностью —81%. Поэтому-то часть сделанных гадалкой предсказаний обычно и сбывается. А легковерные люди и не подозревают, что приобщились к «таинствам» теории вероятностей.

Помимо математической стороны дела, есть и не менее важные причины психологического происхождения. Вот некоторые из них. Прорицатели, как правило, — люди наблюдательные. Вороша карты или перемешивая кофейную гущу, они нет-нет да и ненароком бросят взгляд на доверчивого клиента. Не болезненный ли у него вид («лихой недуг»), не горит ли его взор лихорадочным ожиданием («нечаянная радость»)? Богатый профессиональный опыт подсказывает гадалке, что, кому и как говорить. Не последнюю роль играет и чутье, интуиция. Предсказатели издавна эксплуатируют и то, что человеку' свойственно принимать желаемое за действительное. Оракул так формулирует свое откровение, что понимать его можно самым различным образом — как хочется «заказчику». Вспомним предсказание, сделанное дельфийским оракулом Крезу: «Если ты нападешь на персов, великое государство погибнет». Очень уж хотелось Крезу разрушить чужое государство. Вон он и поверил. А государство-то погибло его собственное.

Из множества сделанных предсказаний люди запоминают обычно лишь те, что сбылись. Несбывшиеся пророчества в памяти людей, как правило, не сохраняются.

Одним из первых ученых, отметивших закономерности в массовых случайных явлениях, был великий французский ученый П. Лаплас. (Кстати, А. Кетле был его учеником). Лаплас просмотрел метрические книги города Парижа с записями о рождении детей с 1745 г. (в этом году впервые начали отмечать в книгах пот младенца) по 1884 г. За это время было зарегистрировано 393 386 мальчиков и 377 555 девочек. Таким образом, на каждые 25 мальчиков приходилось примерно по 24 девочки. Между тем Лаплас знал, что во Франции, а также в большинстве стран Европы и Америки это отношение составляет 22 и 21. Предоставим, но этому поводу слово самому Лапласу: «Когда я стал размышлять об этом, то мне показалось, что замеченная разница зависит от того, что родители из деревни и провинции оставляют при себе мальчиков (мужчина в хозяйстве — более ценная рабочая сила), а в приют для подкидышей отправляют девочек». Изучив списки парижских приютов, Лаплас убедился в справедливости своего предположения: в случайном соотношении пазов новорожденных просматривалась железная закономерность.

Итак, в сложных запутанных массовых явлениях, зависящих от необозримого множества случайных причин, случайность как бы перестает быть случайной. Неопределенность уступает место определенности. Вывод этот настолько ошеломлял, что знаменитый статист К. Пирсон не поленился бросить монету 24 000 раз и … получил 12 012 «гербов», что дает частоту, весьма близкую к 0,5. Закономерность и здесь оказалась вполне определенной.

Вряд ли кто-нибудь из читателей станет повторять вслед за Пирсоном этот весьма нудный и требующий большого времени опыт. (Даже если вы потратите на одно подбрасывание, наблюдение и запись результата всего 3 секунды, то и тогда потребуется не менее трех дней напряженной работы).

С помощью теории вероятностей можно подсчитать вероятность такого, обычно не безразличного нам события, как выигрыш в лотерею.

Вот типичный пример условий денежно-вещевой лотереи. На каждый разряд, включающий 10 000 лотерейных билетов, приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность выиграть деньги, вещь или хоть что-нибудь по одному лотерейному билету? Решение столь простой задачи под силу ученику начальной школы, стоит лишь применить классическую формулу:

Вероятность выиграть деньги = 120/10 000 = 0,012 или 1,2%.

Вероятность выиграть вещь = 80/ 10 000 = 0,008 или 0,8% .

Вероятность выиграть хоть что-нибудь = (120 + 80) / 10 000 = 0,02 или 2% .

В последнем расчете мы суммируем в числителе дроби, так как число благоприятствующих шансов складывается из количества денежных и вещевых выигрышей.

Несколько сложнее дело обстоит со спортивной лотереей. Здесь нс все отдано на откуп случаю: каждый участник может избирать номера для вычеркивания по своему полному усмотрению. Участники спортлото как бы играют друг с другом. Однако, как мы сейчас убедимся, и здесь места для Случая остается вполне достаточно.

Какова, например, при игре в лотерею вероятность вычеркнуть все 6 номеров из 49? Подсчитано, что вычеркивание 6 цифр из 49 может быть произведено почти 14 млн. различных способов (точная цифра 13 983 816). Следовательно, вероятность единственного правильного вычеркивания равна 1/13 983 816=7,2* 10 *, или 7,2 миллионных процента.

Отгадать пять цифр — это значит указать ошибочно одну из шести. Такую ошибку можно сделать 258 способами. Значит, именно таковы шансы, благоприятствующие угадыванию 5 номеров.

А вероятность этого события по классической формуле равна 258/13 983 816 =1,8* 10 ⁵, или 1,8 тысячных процента.

Четыре номера угадает, естественно, значительно больше людей, число благоприятствующих шансов повышается здесь до 13 545. И вероятность соотвегственно будет выше:

13 545/13983816=9,6 10 ⁴, или 9,6 сотых процента.

И, наконец, вероятность угадать три номера равна.

246 280/13983816= 1,8 10 или 1,8 процента.

Все это ничтожно мало.

На непосредственном подсчете основано и свойственное всем людям интуитивное определение вероятности. Скажем, нас спрашивают, что вероятнее, отгадать в лотерею или четыре номера? Мы, не задумываясь, без всякого расчета отвечаем — три. (Правда, мы вряд ли сможем сообразить без расчетов, что для трех номеров вероятность выше почти в 20 раз!).

Интуитивное определение вероятности, выработанное человеком в ходе многовековой эволюции, не раз выручало его в сложных ситуациях. Принимая решение, «что лучше», «что быстрее», «какова мера опасности», люди, сами того не ведая, часто основывают свой выбор на интуитивной вероятностной оценке. «Лучше поездом, чем самолетом». «Поеду-ка я трамваем, автобуса не дождаться». «Сегодня стоит надеть плащ». Во всех этих решениях явно просматривается учет возможности случая.

Интуитивная оценка вероятности, к которой мы часто прибегаем на практике, может служить основой для принятия решений. Делать это, однако следует осмотрительно. Так, во многих рассказах о войне описывается бывалый солдат, который спасает свою жизнь тем, что во время артиллерийского обстрела перебегает от воронки к воронке — прячется там, где только что разорвался снаряд. «Дважды в одну воронку не попадет», — объясняет он. И это кажется правдоподобным. Эта же мысль руководит действиями игроков в рулетку или другие азартные игры, когда они ждут удобного момента, чтобы поставить на какую-нибудь цифру, карту, либо на выпадение «орла» при подбрасывании монеты. «Чем дольше не выпадает, тем шансы выше» — думают они. Да и мы с вами, если нам предлагают на выбор два лотерейных билета, один, скажем, с номером 74 381, а второй 77 777, не задумываясь выбираем первый — может ли быть такая редкая случайность, как выигрыш на билет с пятью семерками.

Все это распространенные заблуждения. Причина их в том, что мы переносим на вероятностные расчеты наш житейский опыт, не имеющий к данному случаю никакого отношения. Нам кажется, что выпадение каких-либо событий исчерпывает их шансы и тем самым уменьшает возможность повторения этих событий в дальнейшем. Между тем, в примерах, которые мы привели, с каждым новым испытанием начинается все сначала, заново. И если эти явления — спасение от снаряда, угадывание номеров при игре в рулетку, падение монеты «орлом», выигрыш по лотерейному билету — действительно случайны, то никакой зависимости между тем, что произошло, и тем, что произойдет в будущем, не существует. Признание противоположного означало бы, что все эти случаи имеют память — запоминают, что было, для того чтобы больше не повторяться. С этим, однако, вряд ли можно согласиться.

Предположим, вы задались целью обязательно решить некую трудную предпринимательскую задачу, например, добиться большой прибыли, выхода на зарубежный рынок, высокого качества производимых товаров.

Задачи такие обычно решаются не сразу, для этого нужно сделать несколько попыток. Вам, конечно, интересно, сколько таких попыток потребуется.

Вероятность самого события можно рассчитать по классической формуле. Так, если вас интересует вероятность получения определенной нормы прибыли, нужно количество случаев, при которых эта прибыль была вами получена, в прошлом (например, четыре раза) разделить на обшее число рассматриваемых случаев (например, 20). Тогда искомая вероятность будет равна 4/20=0,2 или 20%.

Но нас интересует не эта цифра. Наша цель — определить, сколько нужно сделать попыток п (на языке теории вероятностей — сколько нужно провести испытаний), чтобы хотя бы одна из них (больше не требуется) гарантированно дала требуемую норму прибыли.

Для решения этой задачи теория вероятности предлагает простую формулу:

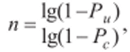
в ней Р_в есть вероятность, с которой мы хотим добиться своей цели — получить нужную норму прибыли, а Р₍ — вероятность самого события — получения требуемой прибыли. По данной формуле рассчитана простенькая, но весьма полезная табличка, позволяющая, наконец, ответить на вопрос, с которого мы начали.

Входя в табличку с нашей вероятностью события — получения прибыли 20% — и задаваясь желаемой вероятностью достижения цели, скажем, 90%, получим требуемое число попыток, равное 10. Это означает, что на 10 попыток хотя бы одна будет наверняка счастливой. Хотите гарантии, близкой к 100% — увеличьте число попыток до 17.

Расчет вероятности интересующего нас события не менее одного раза имеет весьма широкую область применения. Подобные расчеты необходимы, например, при определении качества различных приборов: какова вероятность того, что хотя бы один узел сложного устройства может выйти из строя? С помощью таких расчетов можно также определить, сколько понадобится испытаний, чтобы прийти хотя бы раз к нужному результату (табл. 7.2). Скажем, сколько раз нужно прочитать документ, чтобы хотя бы один раз не пропустить ошибки и т. п.

Таблица 7.2.

Сколько нужно сделать попыток, чтобы добиться цели (хотя бы один раз).

Контрольные вопросы и задания

I .Как рассчитывается вероятность заданного числа будущих событий?

• 2. Как рассчитывается требуемое число попыток?
• 3. Решите следующие две задачи:

Задача № I

Автомобиль снабжен двумя противоугонными приспособлениямимеханическим и электрическим. Каждое из них имеет свою вероятностьсрабатывания. Это не что иное, как надежность. которую можно установить из опыта: сколько раз из ста предохранитель сработает. Так вот. надежность механического приспособления Р_ч = 0.9, а электрического-Р =0.8. Какова же вероятность того, что автомобиль не угонят?

Задача № 2

Наше предприятие собирается приобрести электронный прибор. На прибор дается заводская гарантия. Знающие люди предупредили нас, что в нашем городе сейчас можно приобрести приборы, выпускаемые тремя различными заводами, причем шансы получить прибор завода № 1 равны 0.6, завода № 2 -0,3, а завода № 3 -0,2. Какого завода попадется нам прибор, мы нс знаем; а между прочим, это далеко не безразлично: вероятности того, что прибор проработает без остановки весь гарантийный срок, для каждого завода различны. 11а заводе № 1 -это 0,9, на заводе № 2 -0,8, на заводе № 3 -0,6.

Какова вероятность, что купленный прибор не придется отправлять обратно на завод? Доказано, что вероятность интересующего нас события равна сумме произведения вероятностей получения прибора того или иного завода на соответствующие вероятности их безотказной работы.