Формирование общего приема решения задач на построение

Трудно переоценить роль задач на построение в формировании математического мышления школьников. С древних времен геометрические построения способствовали развитию не только самой геометрии, но и других разделов математики. Задачи на построение циркулем и линейкой и сегодня считаются математически весьма интересными, и вот уже более 100 лет это традиционный материал школьного курса геометрии. Они по своей постановке и методам решения объективно призваны развивать способность отчетливо представлять себе ту или иную геометрическую фигуру и, более того, уметь мысленно оперировать элементами этой фигуры. Задачи на построение могут способствовать пониманию учащимися происхождения различных геометрических фигур, возможности их преобразования — все это является важной предпосылкой становления пространственного мышления школьников, исследовательских и творческих умений, геометрической интуиции. План решения любой задачи на построение — цепочку основных построений, приводящих к цели, можно рассматривать как некоторый алгоритм и, следовательно, их можно использовать и в старших классах как содержательный материал курса информатики и вычислительной техники. В процессе решения задач на построение учитель может эффективно формировать элементы алгоритмической культуры школьников, систематически требуя от них четкой последовательности основных построений. Задачи на построение развивают поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, что очень важно в формировании умений и навыков умственного труда. Посредством задач на построение, и даже самых простейших из них, более глубоко осознаются теоретические сведения об основных геометрических фигурах, так как в процессе решения этих задач ученик создает наглядную модель изучаемых свойств и отношений и работает с этой моделью. Задачи на построение успешно могут быть связаны с такими идеями школьного курса геометрии как преобразования, векторы, координатный метод.

Задачи на построение изучаются в школе в течение трех лет — в 7, 8, 9 классе. Согласно требованиям к математической подготовке учащихся 7—9 классов (11) в результате изучения курса «Геометрия» учащиеся должны овладеть следующими умениями, представляющими обязательный минимум:

• — изображать геометрические фигуры, указанные в условиях теорем и задач, и выделять известные фигуры на чертежах и моделях;
• — проводить доказательные рассуждения в ходе решения типичных задач;
• — вычислять значения геометрических величин (длин, углов, площадей), применяя изученные свойства и формулы;
• — выполнять основные построения циркулем и линейкой, решать несложные комбинированные задачи, сводящиеся к выполнению основных построений;
• — применять аппарат алгебры и тригонометрии в ходе решения геометрических задач;
• — использовать векторы и координаты для решения стандартных задач (вычисление длин и углов, сложение векторов и умножение вектора на число).

На изучение раздела «Основные задачи на построение. Решение задач на построение с помощью циркуля и линейки» учебным планом предусмотрено следующее количество часов:

Окончание таблицы

Примечание: Указания глав и параграфов соответствуют учебнику геометрии (1).

По сетке часов видно, какое место в структуре отдельных тем и даже разделов занимают задачи на построение. Причем, начиная с 7 класса задачи на построение отдельно не рассматриваются, они идут в составе изучаемых тем. Тем самым учителю дается возможность самостоятельно распределять часы внутри темы в зависимости от поставленной задачи и от уровня подготовленности учащихся класса.

Анализ учебников и пособий по геометрии (1, 9) показал, что авторы используют в основном индуктивный путь в изложении материала, относящегося к геометрическим построениям. Учащиеся сначала изучают конкретные виды построений: откладывание на данном луче от его начала отрезка, равного данному; построение угла, равного данному; построение биссектрисы угла; построение перпендикулярных прямых; построение середины отрезка; построение треугольника по трем элементам. Только после этого учащиеся знакомятся с общей идеей геометрического построения в разделе: «Задачи повышенной трудности», где предлагается схема, по которой обычно решают задачи на построение циркулем и линейкой.

Эта схема состоит из четырех частей:

I. Анализ.

II. Построение.

III. Доказательство.

IV. Исследование.

Раскроем их содержание.

I. Анализ — это подготовительный и в то же время наиболее важный этап решения задачи. Целью анализа является установление таких зависимостей между элементами искомой фигуры и данными задачи, которые позволили бы построить эту фигуру. Как правило, анализ задачи состоит в том, что предполагаем ее уже решенной и находим различные следствия (или предпосылки) этого предположения, а затем, в зависимости от вида этих следствий, пытаемся найти путь отыскания решения поставленной задачи. Иначе говоря, «рецепт» прочее ведения анализа состоит в последовательном проведении трех этапов рассуждений:

• 1) Предположим, что задача решена.
• 2) Посмотрим, какие из этого следует извлечь выводы.
• 3) Теперь, сопоставляя полученные выводы, попытаемся найти путь для действительного решения задачи.

II. Построение по намеченному плану.

III. Доказательство того, что построенная фигура удовлетворяет условиям задачи.

IV. Исследование задачи, т. е. выяснение вопроса о том, при любых ли данных задача имеет решение, и если имеет, то сколько решений.

Данная схема имеет свернутый характер. Ее придерживались еще в Древней Греции (IV—III ее до н.э.).

В. С. Крамор (7) предлагает использовать в качестве полной схемы решения задач на построение следующую:

• 1) рассмотрение практической ситуации;
• 2) формулировка задачи;
• 3) анализ задачи;
• 4) составление общего плана решения задачи (указание последовательности решаемых элементарных задач);
• 5) построение фигуры данными инструментами;
• 6) проверка построения фигуры. Доказательство того, что построенная фигура искомая;
• 7) исследование обобщением задачи. В исследование входит поиск условий, при которых задача имеет решение, их количество в каждом из выделенных случаев. Запись условий, при которых задача имеет решение, осуществляется на алгебраическом языке (посредством составления соотношения между заданными элементами);
• 8) решение задачи для каждого из выделенных случаев при исследовании;
• 9) поиск других способов решения, выделение рационального;
• 10) составление других задач, решаемых данным методом. Рассмотрение обобщенных и аналогичных задач.

При составлении плана решения задачи (п. 4) возможны различные способы поиска неизвестных точек и линий, в частности: метод сведения данной задачи к более простой или известной, метод геометрических преобразований и т. д. Для поиска отрезков и углов применяется алгебраический способ. Общий подход к составлению плана действий (наиболее рациональный) следующий: сначала припоминаем все, что известно о данных и искомых элементах фигуры, какие из них можно построить; затем, если их построение не приводит к цели, строим дополнительные элементы (которые могут быть построены при помощи данных) и, наконец, снова анализируем возможности построения искомых элементов. Процесс рассуждения продолжаем до тех пор, пока не получим плана построения фигуры.

Данная схема является, по существу, детализацией традиционной и может быть полезна при обучении решению рассматриваемого вида задач.

В сложившейся практике обучения существуют различные мнения относительно необходимости каждого из четырех этапов (анализ, построение, доказательство, исследование) при решении всех задач на построение, а также формы реализации этих этапов. Так, в соответствия с программой по математике для общеобразовательной школы, в седьмом классе, когда учащиеся впервые начинают знакомиться с умениями решать задачи на построение, анализ и доказательство рекомендуется проводить устно, а элементы исследования могут присутствовать лишь тогда, когда это оговорено условием задачи (11). С другой стороны, в учебнике геометрии (1) указывается, что при решении простейших задач на построение (именно эти задачи изучаются в седьмом классе) отдельные этапы, например, анализ или исследование опускаются: ученикам дается готовый способ построения и готовое доказательство его правомерности. Не все этапы можно соблюдать и при решении задач в восьмом и девятом классах.

Л. А. Черных (15) также считает, что с указанными этапами решения задач на построение учащихся следует знакомить постепенно. При решении несложных задач она рекомендует записывать только построение и доказательство. В более сложных случаях построению должны предшествовать рабочий рисунок и план построения, который следует из анализа. Анализ лучше проводить устно. Устно, под руководством учителя, можно делать и исследование, если в этом есть необходимость.

Мы считаем, что исключение таких этапов как анализ и исследование из процесса решения задач на построение приводит к механическому заучивания данного в готовом виде способа решения, что значительно снижает качество усвоения.

Необходимо отметить, что в методической литературе есть работы, авторы которых пытаются решить проблему эффективного обучения решению задач на построение. Так, обращается внимание на необходимость показать учащимся отличие задач на построение от других видов задач — задача на построение имеет особую структуру: в ней даны геометрические фигуры и условия, связывающие их между собой; требования такой задачи можно разделить на две части: а) построить новую фигуру, связанную с данными фигурами некоторыми условиями, и б) построить определенным набором инструментов (10). При этом в некоторых задачах инструменты указываются (например, построение параллельных прямых с помощью угольника и линейки), а в задачах, где инструменты не указаны, подразумеваются циркуль и линейка. Для более осознанного восприятия содержания задачи рекомендуется обучать учащихся краткой записи того, что дано и что требуется построить. Часть краткой записи «Дано» может быть представлена в разном виде. Так, если даны вид и расположение фигур относительно друг друга, то в «Дано» можно записать только обозначение этих фигур и с помощью имеющихся значков отношения между ними, а сами фигуры изобразить позднее, когда будут выполняться построения. Например, для задачи: «Даны две параллельные прямые и точка на одной из них. Построить окружность, касающуюся этих прямых и проходящую через данную точку», — краткая запись может иметь следующий вид.

Дано: прямые а, Ъ, точка А

А — на, а а | | Ь Построить: окружность О так, чтобы.

• 1) а касалась О
• 2) Ь касалась О
• 3) А находилась на О

В задачах, где даны вид и размеры фигур, без учета их взаимного расположения, в «Дано» следует изобразить и обозначить фигуры. Например, краткая запись задачи «Построить треугольник по двум сторонам и радиусу описанной окружности» может выглядеть так.

Дано:

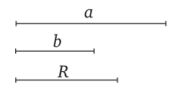
Построить: треугольник АВС так, чтобы.

• 1) ВС = а
• 2) АС = Ъ
• 3) А, В, С — на окружности (О, К)

Некоторые авторы (3, 16), рассматривая приемы решения задач на построение как практические приемы, выделяют четыре этапа их формирования: подготовительный, ознакомительный, формирующий и этап совершенствования умения.

Так, Л. С. Чистякова считает, что учителю первоначально необходимо выявить систему условий, на которую должен опираться ученик для успешного овладения практическим действием. Например, для того чтобы научиться строить с помощью циркуля и линейки угол, равный данному, ученикам необходимо иметь знания о следующих фактах: о данных геометрических фигурах — полупрямой, полуплоскости и угле; о цели действия, в данном случае об угле, равном данному, который требуется построить; о каждой из конструктивных операций и о последовательности их выполнения. Учащиеся должны быть также подготовлены к обоснованиям возможности каждого шага построения и доказательству правильности построения (аксиомы откладывания отрезков и углов, определение равных треугольников, признаках равенства треугольников). Нельзя обойтись и без навыков в выполнении элементарных конструктивных операций: построении окружности произвольного или указанного радиуса с центром в некоторой точке, построение полупрямой, имеющей данное начало и проходящей через данную точку.

Подготовительный этап необходим для актуализации у учащихся указанных предварительных знаний.

На ознакомительном этапе учащиеся должны выделить, что дано, что требуется сделать и какими инструментами, какие операции для этого необходимо выполнить. План рекомендуется показать с помощью рисунков и текста. Например, сначала с помощью кодоскопа на экран проецируется данный угол ВАС, дуга окружности с центром А и полупрямая с началом в точке О (рис. 6.1). На следующих кадрах показывается, как на полупрямой появляется точка В_х (рис. 6.2), а на окружности с центром О радиусом ОВ₁ (ОВ_х = АВ) — точка С_х (рис. 6.3). На заключительном кадре (он здесь не приводится) представлены два треугольника — один (АВС) с данным углом САВ, другой (ОВ₁С₁) с углом С₁ОВ₁, равным данному.

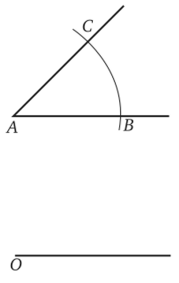
Рис. 6.;

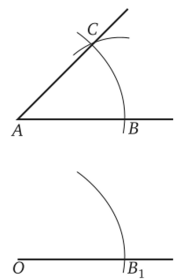
Рис. 6.2.

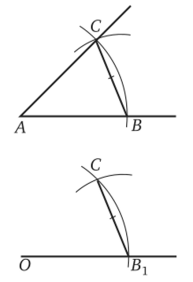
Рис. 6.3.

Далее автор говорит о том, что на ознакомительном этапе должна происходить подготовка к выполнению практического действия с помощью инструментов. Поэтому учащиеся с самого начала не только наблюдают действия учителя, но и выполняют все то, что делает учитель.

На этапе, формирующем умение, учащиеся должны научиться правильно и без посторонней помощи выполнять практическое действие в знакомых условиях, т. е. по образцу. Руководство деятельностью учащихся осуществляется с помощью указанного выше плана (см. рис. 6.1—6.3). При этом вначале заданию сопутствует полный план в виде рисунков и текста-предписания. Затем к заданию прилагается только текстовое предписание. Последние задания учащиеся выполняют полностью самостоятельно.

На последнем этапе — этапе совершенствования практического умения углубляется осознанность умения, отрабатывается автоматизм.

Л. И. Боженкова (3), которая исследовала решение задач на построение методом подобия, так формирует дидактическую цель подготовительного этапа — сформировать у учащихся умения: выделять данные, определяющие единственную фигуру; выделять данные, определяющие форму фигуры, множество пар подобных между собой фигур; строить фигуру по данным, определяющим форму; переходить от построенной фигуры к искомой. После изучения каждого признака подобия автор предлагает набор заданий, обращая внимание на то, что при переходе от одного признака к следующему вопросы несколько усложняются, а именно: расположение треугольников на рисунках меняется, удаляясь от стандартного, варьируется выбор элемента, определяющего единственную фигуру. Ознакомительный этап предназначен для того, чтобы разъяснить учащимся структуру процесса построения методом подобия, назначение каждой операции, составляющей эту структуру. Объяснение она предлагает начать с задачи, в ходе анализа которой учитель предлагает задания-вопросы, ответы на которые кратко фиксируются на доске. Далее составляется план построения и выполняется само построение. После этого учитель обращает внимание учащихся на то, что, выполняя построения, они фактически реализовывали алгоритмическое предписание, которое и предъявляется учащимся в виде следующей блок-схемы:

• 1. Выделить из условия задачи данные, определяющие форму фигуры.
• 2. Выделить данные, определяющие размеры фигуры (линейный элемент).
• 3. Построить фигуру указанной формы, подобную искомой.
• 4. Построить (выделить) отрезок, определяющий размеры фигуры.
• 5. Построить фигуру указанной формы и размеров, используя подобную.
• 6. Полученная фигура является искомой.

Последующая работа направлена на организацию усвоения данного алгоритма как средства решения задач на построение методом подобия.

Попытка выделения общего приема решения задач на построение была предпринята О. Б. Епишевой и В. И. Крупич (6) на примере выполнения построений методом геометрических мест (методом пересечения фигур). Приемы решения задач на построение методом геометрических мест основаны на понятии геометрического места точек. Для решения задач методом геометрических мест необходимо знать основные геометрические места точек.

Материал планиметрии позволяет познакомить учащихся с геометрическим местом точек, удаленных на данное расстояние от точки и прямой; равноудаленных от двух данных точек, от сторон угла, от двух пересекающихся прямых, от двух параллельных прямых и т. д.

Сущность метода геометрических мест при решении задач на построение состоит в следующем.

Пусть, решая задачу, мы должны построить точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть фигура /у, а геометрическое место точек, удовлетворяющее второму условию, есть фигура Р₂. Искомая точка X принадлежит и^и Г₂, т. е. является их точкой пересечения.

Задачи на геометрические места точек можно разделить на два вида. К первому виду относят задачи, в которых дана некоторая фигура и на ней требуется найти точку, удовлетворяющую определенным условиям:

• 1) принадлежит указанной в условии задачи геометрической фигуре;
• 2) принадлежит фигуре, все точки которой обладают определенным свойством.

Ко второму виду относятся задачи, в которых требуется найти точку, удовлетворяющую одновременно двум условиям:

• 1) принадлежит фигуре ^ все точки которой обладают определенным свойством;
• 2) принадлежит фигуре Р₂, все точки которой обладают определенным свойством.

Далее авторами рассматриваются задачи, относящиеся к каждому из двух видов и после этого строится обобщенный прием решения задач каждого из указанных видов.

Так, обобщенный прием решения задач первого вида методом геометрических мест состоит в следующем:

• 1) изобразить геометрическую фигуру, которой принадлежит искомая точка X;
• 2) сформулировать, исходя из текста задачи, условие, которому удовлетворит искомая точка X;
• 3) назвать геометрическое место точек, удовлетворяющих этому условию;
• 4) построить названное геометрическое место точек;
• 5) найти точку (точки) пересечения данной фигуры и геометрического места точек.

Использование понятия геометрического места точек, обладающих определенными свойствами, должно помочь учащимся при нахождении способа решения задач на построение. Так, при анализе двух (на первый взгляд разных) задач: «среди всех точек, равноудаленных от сторон данного угла, найти точку, находящуюся на равных расстояниях от двух данных точек» и «построить окружность, проходящую через две данные точки и касающуюся сторон данного утла», учащиеся должны обнаружить, что эти задачи, по существу, не отличаются друг от друга. Различие между ними состоит в том, что тексты этих задач дают в различной мере указания на те геометрические места точек, с помощью которых данная задача может быть решена. В первой задаче условия, определяющие искомую точку, даны явно в тексте, а во второй задаче их нужно получить, переосмысливая текст задачи.

Таким образом, как показал анализ, делаются попытки найти более рациональный путь обучения решению задач на построение вообще и с помощью конкретных методов — метода геометрических мест, подобия — в частности. Авторы стремятся выделить общие моменты построения. Однако на основной вопрос — почему именно так необходимо выполнять построение — ответа не дается.

В существующих учебниках каждая задача на построение дается обособленно, вне связи с другими, несмотря на то, что авторами задается продуманная последовательность этих задач. Поскольку при решении каждой последующей задачи в большинстве случаев нет опоры на уже решенную, качество выполнения задач на построение не улучшается. Для каждого построения дается частный прием его совершения. Причем главным в действиях учащихся является исполнительная часть: ученики механически производят построения, не имея полной и адекватной ориентировочной основы.

Учащиеся часто не понимают, что при решении почти всех основных задач на построение с помощью циркуля и линейки, предусмотренных школьной программой, используется деятельность с аналогичным содержанием, но с измененной последовательностью операций. Сравним, например, последовательность операций, выполненных учениками при решении следующих трех задач (табл. 6.1).

Таблица 6. 7.

	Задача I.	Задача II.	Задача III.

Задача I: деление отрезка пополам.

Задача П: построение перпендикуляра к прямой, проходящего через точку, данную на этой прямой.

Задача III: построение перпендикуляра к прямой, проходящего через точку, данную вне этой прямой.

Из таблицы (табл. 6.1) видно, что первая операция в задачах II и III необходима для выделения определенного отрезка на данной прямой а: во второй задаче путем откладывания от данной точки О равных отрезков ОА и ОС, в задаче III — через построение окружности с центром в данной точке В, пересекающей прямую, а в двух точках, А и С. Далее задачи II и III фактически свелись к задаче I. Поэтому для этих задач вторая операция совпадает с первой операцией задачи I, когда строят две окружности с центрами в точках, А и С, радиусом АС и находят точки пересечения В и D этих окружностей. Третья операция задач II и III аналогична второй операции задачи I, когда проводят прямую ВД, пересекающую данную прямую (данный отрезок) в точке О. Операции три для задачи I и четыре для задач II и III идентичны и необходимы для доказательства правомерности выбранного метода построения.

В сложившейся практике обучения каждая из указанных выше задач воспринимается учениками как самостоятельная.

Приведем еще один пример: научившись строить биссектрису данного угла и переходя к задаче построения перпендикуляра к прямой, проходящего через точку, данную на прямой, учащиеся рассматривают вторую задачу как новую, не замечая, что она сводится к первой, так как перпендикуляр в этой задаче можно рассматривать как биссектрису развернутого угла с вершиной в данной точке прямой.

Хотя многие методисты и учителя отмечают, что самым важным и трудным этапом решения является анализ, учащимся не раскрывается полная система ориентиров, реализация которых помогла бы им найти «ключ» к решению конкретной задачи, в чем и состоит цель этого этапа. Анализ рекомендуется начинать с того, что ученик делает рисунок согласно условию задачи, а затем по этому рисунку ищет путь решения задачи. Однако от ученика остается скрытым, почему он должен делать именно такой рисунок, на что он должен ориентироваться, когда при построении той или иной фигуры строит те точки, которые указаны в учебнике, и т. д. Другими словами, анализа как нахождения элементов искомой фигуры по заданным элементам данной фигуры не осуществляется. Как уже было отмечено выше, в большинстве учебников при решении основных задач на построение с помощью циркуля и линейки (их часто называют простейшими задачами) авторы вообще не рекомендуют проводить анализ. Вот, например, как излагается способ решения первой из задач на построение: «на данном луче от его начала отложить отрезок, равный данному» (1).

«Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ (рис. 6.4, а). Затем циркулем построим окружность радиусом АВ с центром О (рис. 6.4, б). Эта окружность пересечет луч ОС в некоторой точке Д. Отрезок ОД — искомый» (1, с. 43).

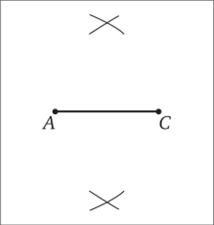
Рис. 6.4.

Ученику таким образом показывается, что нужно построить (конечный результат действия) и ряд последовательных операций, с помощью которых этот результат получается, т. е. только исполнительная часть действия. Ученику остается только запомнить эту последовательность. Потом ученик воспроизводит предлагаемый способ, но не может ответить на вопросы: сколько точек необходимо построить, чтобы воссоздать данный отрезок; почему для построения отрезка, равного данному, достаточно построить две точки — его граничные точки; почему для нахождения расположения одной из точек строим окружность, радиус которой равен данному отрезку, и т. п. Это свидетельствует о том, что воспроизведение исполнительных операций не сопровождается осознанием оснований для выполнения этих действий.

Не отрицая необходимости и значимости анализа, исследования и доказательства как этапов решения задач на построение, мы попытались выделить общую ориентировочную основу, помогающую ученику разумно и осознанно проводить такой теоретический анализ и исследование задачи, которые открывали бы путь к самостоятельному нахождению рационального способа решения ее в противовес заучивания и воспроизведению готового, данного в учебнике.

Анализ показал, что все задачи на построение с помощью циркуля и линейки сводятся в конечном счете к построению ограниченного числа фигур: точки, отрезка и окружности. В свою очередь, для построения отрезка и окружности достаточно выделить точки, их определяющие. С другой стороны, построение фигуры, обладающей заданными свойствами (это является требованием любой задачи на построение), также сводится к построению определяющих ее точек (характеристических точек этой фигуры). При этом для всех задач сам способ построения точки как геометрической фигуры идентичен: необходимо найти пересечение двух линий — прямой и прямой, прямой и окружности, двух окружностей. Ученик должен понимать, какие точки и сколько необходимо выделить для искомой фигуры, чтобы потом, построив эти точки, можно было воссоздать требуемую фигуру в целом.

Нам представляется, что важным моментом нахождения способа решения задачи на построение является обязательное выполнение анализа задачи, независимо от степени ее сложности. При этом форма проведения анализа может быть различной: теоретическое рассуждение в форме устной или письменной речи или рассуждение, сопровождаемое чертежом. Основное назначение анализа — выявить, «открыть» те знания и умения, которые могут быть в явном виде не заданы в условии задачи, но которые необходимы для осознанной разработки плана построения.

По нашему мнению, анализ должен сочетаться с исследованием, включающим в себя ответы на следующие вопросы:

• 1) всегда ли возможно построение при данных условиях,
• 2) является ли данное решение единственным или возможно несколько решений,
• 3) какие из ранее изученных задач на построение могут быть использованы в качестве промежуточных построений,
• 4) к какой из ранее изученных задач на построение может быть сведена данная задача.

Включение в исследование, кроме пунктов 1 и 2, которые традиционно составляют содержание этого этапа решения задач на построение, пунктов 3 и 4 будет способствовать пониманию эквивалентности ряда задач, обеспечению преемственности изучаемых знаний, повышению качества их усвоения, а главное, разумному решению задачи. Так, например, необходимо обратить внимание учащихся на эквивалентность таких задач, как «разделить данный угол пополам» и «построить биссектрису данного угла»; «построить перпендикуляр к данной прямой, проходящий через точку, заданную на этой прямой» и «построить биссектрису развернутого угла с вершиной в данной точке»; «разделить отрезок пополам» и «построить серединный перпендикуляр к данному отрезку» и т. д.

В сложившейся практике обучения исследование если и рекомендуется проводить, то после уже выполненного построения и причем по отношению не ко всем задачам. Мы считаем, что исследование, как и анализ, должны быть одними из начальных неотъемлемых компонентов деятельности по решению задач на построение.

Учитывая все вышесказанное было выделено содержание общего приема решения задач на построение с помощью циркуля и линейки, включающее следующие компоненты:

• 1. Выделить геометрические фигуры, данные в условии задачи, и отношения между ними.
• 2. Выделить геометрическую фигуру, которую необходимо построить (искомая фигура).
• 3. Выделить из условия задачи, какими свойствами должна обладать искомая фигура.

• 4. Дать определение искомой фигуры (назвать необходимые и достаточные признаки соответствующего понятия).
• 5. Выделить точки, необходимые и достаточные для построения искомой фигуры (определяющие точки).
• 6. Перечислить знания, с помощью которых можно обеспечить требуемые условием задачи свойства искомой фигуры.
• 7. Установить достаточность или недостаточность данных условий для построения искомой фигуры.
• 8. Установить, за какими знаниями могут быть «скрыты» те, которые необходимы для построения искомой фигуры.
• 9. Выбрать знания, которые будут использованы для построения искомой фигуры и объяснить правомерность такого выбора.
• 10. Установить возможность построения искомой фигуры по данным условиям задачи:
  • а) всегда ли возможно построение при данных условиях,
  • б) является ли выбранный способ решения задачи единственным или возможно несколько решений,
  • в) какие из ранее известных задач на построение могут быть использованы в качестве промежуточных построений,
  • г) к какой из ранее изученных задач на построение может быть сведена данная задача.
• 11. Выбрать способ построения каждой из определяющих точек искомой фигуры: пересечение или двух прямых, или прямой и окружности, или двух окружностей.
• 12. Построить каждую из определяющих точек искомой фигуры и по ним фигуру в целом.
• 13. Доказать, что построенная фигура удовлетворяет условиям задачи.

Предлагаемый прием включает общие, базовые действия. Естественно, что при решении конкретных задач некоторые из этих компонентов будут опускаться. Так, например, решение первых задач на построение не требует исследования на возможность сведения их к ранее изученным. Не всегда необходим анализ условия задачи с целью выявления «скрытых» за ним нужных знаний и умений — заданной в явном виде информации вполне достаточно для составления плана решения и его реализации.

Покажем реализацию общего приема на примере конкретных задач. Для сравнения приведем изложение соответствующего материала в одном из принятых в школе учебников геометрии (1). В качестве примера рассмотрим первую из задач на построение, с которой знакомятся учащиеся средней школы: «на данном луче от его начала отложить отрезок, равный данному». Содержание способа выполнения этого построения, предлагаемое в учебнике, приведено выше. Опишем, как учитель может организовать работу учащихся по решению указанной задачи, используя предлагаемый нами общий прием.

1. Выделить геометрические фигуры, данные в условии задачи, и отношения между ними.

Учитель: Что дано в условии задачи?

Ученик: Две геометрические фигуры: отрезок и луч.

Учитель: Указаны ли в условии задачи длина отрезка, расположение отрезка и луча?

Ученик: Нет, не указаны.

Учитель: Как по-вашему, можем ли мы взять отрезок произвольной длины и расположить отрезок и луч на плоскости листа бумаги также произвольно?

Ученик: Да, можем.

Учитель: Запишем, что дано в данной задаче. (.Учитель на доске, а ученики в тетрадях чертят и записывают.).

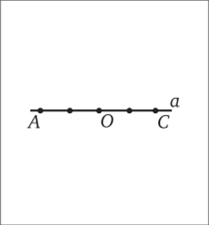
Дано:

отрезок АВ

луч ОС.

2. Выделить геометрическую фигуру, которую необходимо построить (искомая фигура).

Учитель: Какую фигуру требуется построить?

Ученик: Отрезок.

• (Учитель сообщает, что фигуру, которую требуется построить, называют «искомой» фигурой.)
• 3. Выделить из условия задачи, какими свойствами должна обладать искомая фигура.

Учитель: Какими свойствами должен обладать отрезок, который надо построить?

Ученик: Этот отрезок должен обладать двумя свойствами: 1) быть равным данному отрезку АВ и 2) отрезок должен быть отложен от начала О данного луча ОС.

Учитель: Правильно, теперь можем записать, что требуется построить. (Учитель на доске, а ученики в тетрадях записывают.)

Построить: отрезок ОД так, чтобы.

• 1) ОД = АВ,
• 2) точки О и, А совпадали,
• 3) точка Д находилась на луче ОС.
• 4. Дать определение искомой фигуры (назвать необходимые и достаточные признаки соответствующего понятия).

Учитель: Какими существенными свойствами должна обладать геометрическая фигура, чтобы ее можно было назвать отрезком? Ученик: Эта фигура должна обладать двумя существенными свойствами:

1) быть частью прямой и 2) эта часть прямой должна быть ограничена с двух сторон, то есть иметь две граничные точки.

Учитель: Правильно.

5. Выделить точки, необходимые и достаточные для построения искомой фигуры (определяющие точки).

Учитель: Сколько точек и какие надо построить, чтобы по ним можно было построить требуемый отрезок?

Ученик: Для построения данного отрезка достаточно построить две точки — его граничные точки, а потом соединить их прямой линией.

Учитель: Почему достаточно только этих точек?

Ученик: Отрезок — это часть прямой линии. Для построения прямой надо построить любые две точки и через них провести линию, т. к. через две точки проходит одна и только одна прямая. Значит, и для отрезка достаточно двух точек, но эти точки будут не любые, а определенные — начало и конец отрезка.

• 6. Перечислить знания, с помощью которых можно обеспечить требуемые условием задачи свойства искомой фигуры.
• 7. Установить достаточность или недостаточность данных условия для построения искомой фигуры (в данной задаче эти два компонента целесообразнее объединить).

Учитель: Имеются ли в условии задачи все данные, необходимые для построения отрезка, равного данному?

Ученик: Часть прямой дана, потому что дан луч ОС, который сам является частью прямой, имеющей одну граничную точку О. Также можно построить одну из точек искомого отрезка — это будет точка, которая совпадает с началом луча О, так как по условию отрезок надо откладывать от начала луча. Осталось найти способ построения второй граничной точки искомого отрезка.

8. Установить, за какими знаниями могут быть «скрыты» те, которые необходимы для построения искомого отрезка.

Учитель: Какое условие задачи «помогает» найти способ построения второй граничной точки?

Ученик: Условие, что искомый отрезок должен быть равен данному.

9. Выбрать знания, которые будут использованы для построения искомой фигуры и объяснить правомерность такого выбора.

Учитель: Что означает, что один отрезок равен другому?

Ученик: Это означает, что эти отрезки имеют равные длины, что они совмещаются при наложении…

Учитель: Как проверить, что два отрезка имеют равные длины; с помощью какого инструмента мы можем в этом убедиться?

Ученик: С помощью циркуля.

Учитель: Почему мы не можем использовать линейку?

Ученик: Как Вы уже нам объясняли, линейка может служить для выполнения разных задач. Например, с помощью линейки можно проводить прямые и ломаные линии, строить треугольники, четырехугольники и другие геометрические фигуры, состоящие из отрезков.

С другой стороны, если на линейке нанесены меры длины, то она может служить для измерения отрезков. В задачах на построение мы используем линейку без масштабных делений, то есть с помощью такой линейки мы можем только проводить прямые линии, но не измерять. Поэтому для построения равных отрезков надо использовать циркуль.

Учитель: Почему именно циркуль?

Ученик: Потому что с помощью циркуля мы можем построить окружность или ее часть — дугу.

Учитель: Какое свойство окружности помогает найти положение второй граничной точки искомого отрезка?

Ученик: Только у этой фигуры все точки находятся на одинаковом расстоянии от центра. Поэтому, если мы пересечем окружностью с центром в точке О и радиусом АВ луч ОС, то получим вторую граничную точку.

Учитель: Как вы считаете, какую фигуру — окружность или дугу лучше использовать в данной задаче при построении равных отрезков?

Ученик: Поскольку луч в данной задаче выбран произвольно, то он может занимать различное положение: быть направлен вверх или вниз, вправо или влево. Вот почему в этой задаче для выделения равных отрезков, независимо от положения луча, следует проводить окружность, чтобы учесть всевозможные положения его. Если бы положение луча было строго определено, то достаточно было бы провести часть этой окружности — дугу, пересекающуюся с данным лучом. Конечно, и здесь мы могли бы построить окружность, но строим дугу с единственной целью — чтобы не загромождать чертеж.

10. Установить возможность построения искомой фигуры по данным условиям задачи.

Учитель: Всегда ли можно построить отрезок, равный данному, исходя из условия этой задачи?

Ученик: Построение всегда возможно.

11. Выбрать способ построения каждой из определяющих точек искомой фигуры.

Учитель: Итак, какой из известных вам способов построения точки — пересечение прямой и прямой, прямой и окружности, двух окружностей — выбирается для построения второй граничной точки искомого отрезка?

Ученик: Вторую граничную точку находим путем пересечения луча ОС (прямой) окружностью.

Учитель: Правильно. Выполните и опишите построение.

12. Построить каждую из определяющих точек искомой фигуры и по ним фигуру в целом.

Ученик: 1) Раствором циркуля измеряем длину данного отрезка АВ. Ножки циркуля будут как бы «границами» искомого отрезка. 2) Одну ножку циркуля ставим в точку О, потому что по условию задачи искомый отрезок должен откладываться от начала данного луча ОС. 3) Проводим окружность с центром в точке О и радиусом, равным длине данного отрезка АВ. 4) Точку пересечения окружности и луча обозначим Д. Отрезок ОД будет искомым.

13. Доказать, что построенная фигура удовлетворяет условиям задачи.

Учитель: Почему именно отрезок ОД будет той геометрической фигурой, которую необходимо было построить?

Ученик: Фигура ОД будет искомым отрезком потому, что.

• а) это часть прямой и двумя граничными точками О и Д,
• б) длина отрезка ОД равна длине данного отрезка АВ.

Учитель: Правильно, решение задачи закончено.

Приведем еще один пример решения задачи на построение с помощью общего приема.

ЗАДАЧА: Построить биссектрису данного угла.

В учебнике геометрии решение данной задачи излагается в следующем виде (1, с. 44—45).

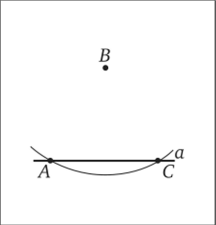
Рис. 6.5.

«Проведем окружность произвольного радиуса с центром в вершине А данного угла. Она пересечет стороны угла в точках В и С (рис. 6.5). Затем проведем две окружности одинакового радиуса ВС с центром в точках В и С (на рисунке изображены лишь части этих окружностей). Они пересекутся в двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е. Докажем, что луч АЕ является биссектрисой данного угла.

Рассмотрим треугольники АСЕ и ABE. Они равны по трем сторонам. В самом деле, АЕ — общая сторона; АС и АВ равны, как радиусы одной и той же окружности; СЕ = ВЕ по построению. Из равенства треугольников АСЕ и ABE следует, что угол CAE = углу ВАЕ, т. е. луч АЕ — биссектриса данного угла".

Не акцентируя внимания на анализе предлагаемого пути обучения решению рассматриваемой задачи, покажем, как выглядит ход ее решения при использовании общего приема (будем указывать лишь номера компонентов приема и их реализацию).

1. Дан угол ВАС

Рис. 6.6.

• 2. Надо построить биссектрису.
• 3. Биссектриса данного угла ВАС.
• 4. Биссектриса — это
• а) луч, исходящий из вершины угла, и
• б) делящий его на два равных угла.
• 5. Биссектриса как геометрическая фигура имеет две определяющие точки: одна — вершина угла, другая — любая точка внутри угла на луче, выходящем из вершины угла.
• 6. Из определения биссектрисы следует, что для ее построения необходимо построить два равных угла, имеющих общую вершину и общую сторону.
• 1) Два угла называются равными, если их можно совместить наложением.
• 2) В равных треугольниках против равных сторон лежат равные углы.
• 3) Признаки равенства треугольников:
  • а) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
  • б) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
  • в) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
• 7. Недостаточно, т. к. в явном виде не дается информация, необходимая для выполнения построения.
• 8; 9. Для построения будем использовать знания 6.2 и 6.3 в, т. к. при сопоставлении с условием задачи и свойствами той фигуры, которую необходимо построить, выделенные знания подсказывают путь решения через построение равных треугольников по трем сторонам с одной общей стороной и общей вершиной.

Выбираем третий признак равенства треугольников потому, что его реализация предусматривает построение соответственно равных отрезков. Способ построения равных отрезков был изучен ранее.

• 10. Построение возможно по данным условия задачи. При решении данной задачи могут быть использованы знания о построении равных отрезков.
• 11. Для построения определяющих точек как геометрических фигур применимы способы пересечения прямой и окружности и двух окружностей.
• 12. Для построения двух равных углов с общей вершиной и общей стороной надо построить два равных треугольника с общей стороной и общей вершиной, в состав которых будут входить эти углы. Поскольку величины сторон этих треугольников нам не даны, их можно выбирать произвольно. Построение будем выполнять следующим образом:
• 1) На сторонах АС и АВ данного угла ВАС от вершины А откладываем равные отрезки АМ и АЕ. Для этого проводим окружность произвольного радиуса с центром в точке Л (рис. 6.7).

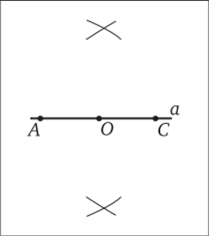
Рис. 6.7

Таким образом получили по одной паре соответственно равных сторон строящихся треугольников и тем самым определили положение двух вершин каждого из треугольников — А и М, А и Е.

2) Для получения еще одной пары соответственно равных сторон и тем самым определения положения третьей вершины треугольников должны отложить равные отрезки от точек М и Е.

Для этого с центром в точках М и Е проводим окружности одинакового радиуса. Установление положения третьей вершины строящихся треугольников зависит от взаимного расположения проводимых окружностей, которое определяется выбранной величиной радиуса.

Если радиусы будут меньше половины отрезка МЕ, то окружности не пересекутся друг с другом и построение невозможно (рис. 6.8, а).

Если радиус будет равен половине отрезка МЕ, то две окружности будут касаться (рис. 6.8, б). Точка касания К этих окружностей будет третьей вершиной строящихся треугольников.

Если радиус окружностей будет больше половины отрезка МЕ, но меньше АМ = АЕ, то окружности будут пересекаться в двух точках К и Н, лежащих внутри угла САБ (рис. 6.8, в). За третью вершину строящихся треугольников можно выбрать любую из этих точек. Решение задачи возможно.

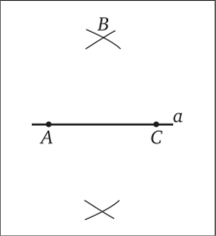
Рис. 6.8.

Если радиус окружностей будет равен AM = АЕ, то окружности также будут пересекаться в двух точках К и Я, при этом точка К лежит внутри угла САВ, а точка Я совпадает с вершиной А угла САВ (рис. 6.8,.

г). Третьей вершиной треугольников будет точка К. Решение задачи возможно.

И, наконец, если радиус окружностей будет больше AM = АЕ, то окружности будут пересекаться в двух точках К и Н, при этом точка К лежит внутри угла САВ, а точка Я — вне угла САВ (рис. 6.8, д). В качестве третьей вершины строящихся треугольников берем точку К, т. к. по определению биссектриса угла должна лежать внутри данного угла. Решение задачи возможно.

Таким образом, для построения второй пары соответственно равных сторон треугольников и определения положения их третьей вершины возможно использование различных вариантов. Выбираем последний вариант (рис. 6.8, д).

3) В соответствии с выбранным вариантом строим МК =ЕК (рис. 6.9).

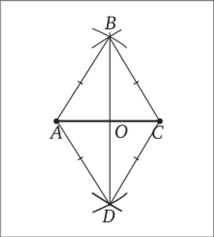
Рис. 6.9.

4) Из вершины, А через точку К проводим луч АК (рис. 6.10). Таким образом, построили два равных треугольника МАК и КАЕ с общей вершиной А и общей стороной АК. Следовательно, угол МАК = углу КАЕ как углы, лежащие против равных сторон. Значит, АК — биссектриса угла САБ.

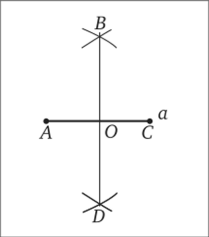
Рис. 6.10.

13. Построенная фигура АК искомой фигурой биссектрисой данного угла САВ, так как а) это луч АК, выходящий из вершины угла САВ, и б) этот луч делит угол САВ на два равных угла.

Усвоение умения строить биссектрису данного угла открывает учащимся возможность для самостоятельного решения следующих задач на построение: построить прямой угол; в данной точке прямой провести перпендикуляр к ней. Действительно, способ построения биссектрисы угла не зависит от величины этого утла, от годится для любых видов углов, в том числе и развернутого. С другой стороны, перпендикуляром к прямой называется луч, проведенный из точки на прямой и образующий с ней прямые углы, т. е. углы, равные половине развернутого угла.

В связи с этим было бы целесообразно при решении задачи на построение биссектрисы данного угла предлагать учащимся углы различной величины. Это способствовало бы обобщению усваиваемого метода решения, установлению связей между различными задачами на построение, по своей формулировке не совпадающих с исходной задачей, но имеющих один и тот же путь решения.

Таким образом, как видно из приведенных выше примеров, использование общего приема решения задач на построение позволяет научить учащихся осуществлять анализ условия задачи, выявлять знания, необходимые для построения искомой фигуры, выбирать рациональный способ построения каждой определяющей точки фигуры и по ним фигуры в целом, доказывать правомерность предлагаемого пути решения задачи.

На примере нескольких задач учитель может разъяснить учащимся содержание общего приема, назначение каждого из компонентов и процедуру использования этого приема. Затем организовать усвоение содержания этого приема в соответствии с принципами деятельностной теории учения (4, 14).

Овладение общим приемом решения задач на построение будет способствовать разумному, сознательному и самостоятельному нахождению учащимися способа построения требуемой геометрической фигуры.

• 1. Атанасян, Л. С. Геометрия: учебник для 7—9 кл. сред. шк. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев [и др.]. — М.: Просвещение, 1990.
• 2. Болтянский, В. Г. Анализ — поиск решения задачи / В. Г. Болтянский // Математика в школе. — 1974. — № 1.
• 3. Боженкова Л. И. Алгоритмический подход к задачам на построение методом подобия / Л. И. Боженкова // Математика в школе. — 1991. — № 2.
• 4. Гальперин, П. Я. Методы обучения и умственное развитие ребенка / П. Я. Гальперин. — М.: Изд-во Московского унта, 1985.
• 5. Геометрические построения: методическая разработка. — М., 1987.
• 6. Епишева, О. Б. Учить школьников учиться математике / О. Б. Епишева, В. И. Крупич. — М.: Просвещение, 1990.
• 7. Крамор, В. С. О совершенствовании методов обучения математике / В. С. Крамор. — М.: Просвещение, 1989.
• 8. Мехтиев, М. Г. Задачи на построение циркулем и линейкой. Часть 1 / М. Г. Мехтиев. — Махачкала: Дагучпедгиз, 1990.
• 9. Погорелое, А. В. Геометрия: учебник для 7—11 кл. сред. шк. / А. В. Погорелов. — М.: Просвещение, 1990.

• 10. Построение и преобразования в курсе геометрии средней школы: метод, пособие для физ.-мат. фак. пед. ин-тов. — Сыктывкар: Коми ГПИ, 1992.
• 11. Программа средней общеобразовательной школы. Математика. — М.: Просвещение, 1991.
• 12. Рыжик, В. И. Система задач школьного курса геометрии: дис. … д-ра пед. наук / В. И. Рыжик. — Санкт-Петербург, 1993.
• 13. Старовойтова, Т. С. Готовым знаниям к применению / Т. С. Старовойтова, Г. Е. Шляхтер // Математика в школе. — 1990. — № 3.
• 14. Талызина, Н. Ф. Управление процессом усвоения знаний / Н. Ф. Талызина. — М.: Изд-во Московского унта, 1984.
• 15. Черных, Л. А. Использование классной доски на уроках геометрии / Л. А. Черных // Математика в школе. — М., 1989. — № 2.
• 16. Чистякова, Л. С. Приемы формирования практических умений и навыков при обучении геометрии / Л. С. Чистякова // Математика в школе. — М., 1987. — № 4.