Формула полной вероятности. 
Формула Байеса

Следствием двух основных теорем теории вероятностей — теоремы сложения и теоремы умножения — являются формула полной вероятности и формула Байеса.

Теорема. Если событие Т⁷может произойти только при условии появления одного из событий (гипотез) А_{, А₂, …, А_п, образующих полную группу, то вероятность события Еравна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события Р:

? По условию события (гипотезы) А_Х, А₂,…"А_п образуют полную группу, следовательно, они единственно возможные и несовместные (рис. 1.8).

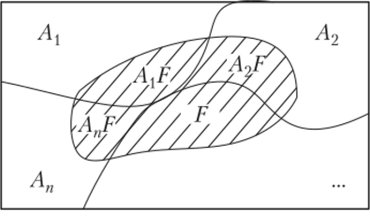
Рис. 1.8.

Так как гипотезы Л, Л₂, А_п — единственно возможные, а событие Б по условию теоремы может произойти только вместе с одной из гипотез (см. рис. 1.7), то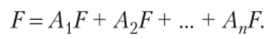

В силу того что гипотезы А_[у А₂, …, А_п несовместны, можно применить теорему сложения вероятностей: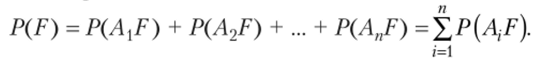

По теореме умножения 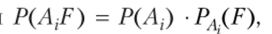откуда и получается утверждение (1.31). ?

Формула (1.31) называется формулой полной вероятности. В частности, для противоположных событий (гипотез) А и А, образующих полную группу, формула (1.31) примет вид.

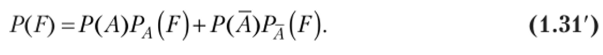
Следствием теоремы умножения и формулы полной вероятности является формула Байеса.

Она применяется, когда событие Р, которое может появиться только с одной из гипотез А _и А₂,…, А_п, образующих полную группу событий, произошло и необходимо произвести количественную переоценку априорных вероятностей этих гипотез Р (А_{), Р (А₂), …, Р (А_п)> известных до испытания, т. е. надо найти апостериорные (получаемые после проведения испытания) условные вероятности гипотез Р_Р(А_{), Р_Р(А₂)_У…, Р_Р(А_п).

? Для получения искомой формулы запишем теорему умножения вероятностей событий Р и А^ в двух формах:

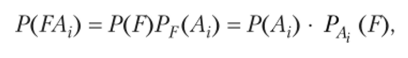
откуда

или с учетом формулы (1.31).

Формула (1.33) называется формулой Байеса, или теоремой гипотез.

Значение формулы Байеса состоит в том, что при появлении события Б> т. е. по мере поступления данных, получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы (принятые решения, предполагаемые модели), основываясь на переходе от их априорных вероятностей к апостериорным (рис. 1.9). Чем ближе условные вероятности Р_р (Д) к единице, тем более обоснованными считаются принятые решения.

Рис. 1.9.

Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т. п.

Замечание. Если условные вероятности Р_Л. (Е)(/ = 1,2,…, п) равны, т. е. на вероятность события Р все гипотезы влияют одинаково, то согласно формуле Байеса (1.33) получаем Р_р (Д) = Р (Д), т. е. дополнительная информация о появлении события Р не имеет никакой ценности, поскольку не меняет наших представлений об априорных вероятностях гипотез. Если вероятности гипотез Р (Д) (г = 1, 2,…, п) одинаковы (в ряде случаев такое предположение возможно, если эти вероятности неизвестны), то.

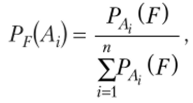
т.е. апостериорные вероятности прямо пропорциональны соответствующим условным вероятностям Р_Л .(Р) события Р.

О Пример 1.34а. В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98, 88 и 92% случаев.

• 1) Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.
• 2) Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?

Решение. 1) Обозначим события:

А, — телевизор поступил в торговую фирму от г-го поставщика (г-1,2,3);

Р — телевизор не потребует ремонта в течение гарантийного срока.

По условию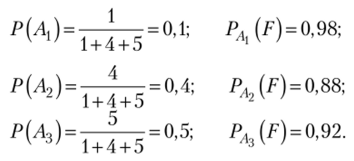

По формуле полной вероятности (1.31).

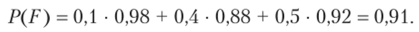
2) Событие .Р — телевизор потребует ремонта в течение гарантийного срока;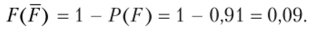

По условию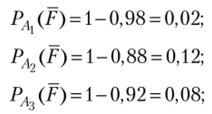

По формуле Байеса (1.32).

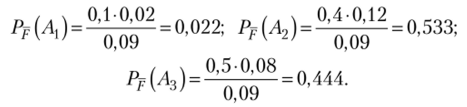
Таким образом, после наступления события Р вероятность гипотезы Л₂ увеличилась с Р (А₂) = 0,4 до максимальной Рр (А₂) = 0,5.33, а гипотезы Л₃ — уменьшилась от максимальной Р (А₃) = 0,5 до Р-(А₃) = 0,444, если ранее (до наступления события Р) наиболее вероятной была гипотеза Л₃, то теперь, в свете новой информации (наступления события Р), наиболее вероятна гипотеза А₂ — поступление данного телевизора от 2-го поставщика. ?

О Пример 1.35. Известно, что в среднем 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она нестандартна. Определить вероятность того, что: 1) взятое наудачу изделие пройдет упрощенный контроль; 2) изделие стандартное, если оно: а) прошло упрощенный контроль; б) дважды прошло упрощенный контроль.

Решение. 1) Обозначим события:

Л, А₂ — взятое наудачу изделие соответственно стандартное или нестандартное;

/•' — изделие прошло упрощенный контроль.

По условию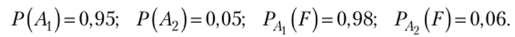

Вероятность того, что взятое наудачу изделие пройдет упрощенный контроль, но формуле полной вероятности (1.31).

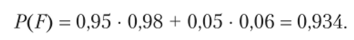
2, а) Вероятность того, что изделие, прошедшее упрощенный контроль, стандартное, по формуле Байеса (1.32):

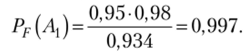
2, б) Пусть событие I⁷* — изделие дважды прошло упрощенный контроль. Тогда по теореме умножения вероятностей.

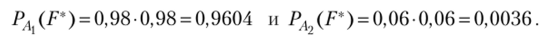
По формуле Байеса (1.33).

Так как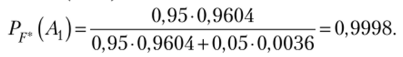

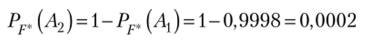
очень мала, то гипотезу А-> о том, что изделие, дважды прошедшее упрощенный контроль, нестандартное, следует отбросить как практически невозможное событие. ?

1> Пример 1.36. Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго — 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит: а) 1-му стрелку; б) 2-му стрелку?

Решение. Обозначим события:

А — оба стрелка не попали в мишень;

А₂ — оба стрелка попали в мишень;

Л₃ — 1-й стрелок попал в мишень, 2-й нет;

А_а — 1-й стрелок нс попал в мишень, 2-й попал;

Р — в мишени одна пробоина (одно попадание).

Найдем вероятности гипотез и условные вероятности события Р для этих гипотез:

Теперь по формуле Байеса (1.33).

т.е. вероятность того, что попал в цель 1-й стрелок при наличии одной пробоины, в 6 раз выше, чем для второго стрелка. ?

[> Пример 1.36а. Компания по страхованию автомобилей разделяет водителей на три класса, которые включают 20%, 50% и 30% водителей соответственно. Вероятности того, что в течение года водитель попадает в аварию, равны 0,01, 0,03 и 0,1 соответственно для каждого класса. Наугад выбранный водитель два года подряд из пяти лет срока страховки попадал в аварию. Какова вероятность того, что он относится: а) к первому классу; б) к третьему классу?

Решение. Обозначим события:

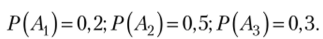
Л], А₂, А₃ — водитель соответственно первого, второго и третьего класса; Р — водитель два года подряд из пяти лет срока страховки попадал в аварию.

По условию Найдем условные вероятности события Р (учитываем, что из пяти лет водитель три года не попадал в аварию, два года — попадал, причем попадал два года подряд, что дает четыре варианта (по годам 1—2, 2—3, 3—4, 4—5)):

По формуле Байеса (1.33).

т.е. после наступления события Р гипотеза Л, практически невозможна и должна быть отвергнута. ?