Плотность вероятности двумерной случайной величины

Определение. Двумерная случайная величина (X, У) называется непрерывной, если ее функция распределения F (x, у) — непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная F" _y[x, y).

Аналогично одномерному случаю вероятность пары отдельно взятых значений двумерной непрерывной случайной величины равна нулю, т. е. Р (Х - х_ь У = у_х) = 0. Это вытекает непосредственно из формулы (5.10) при х₂ —у₂ ->у t с учетом непрерывности функции распределения F (x, у).

Для двумерной случайной величины, так же как и для одномерной, вводится понятие плотности вероятности.

Найдем вероятность попадания случайной точки (X, У) в прямоугольник со сторонами Дх и Ду, т. е.

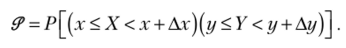
Полагая в формуле (5.10) х, =х, х₂ = х + Ах, у_х — у, у₂ — у + Ду, получим, что эта вероятность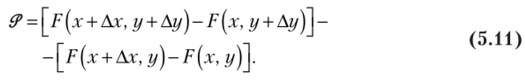

Средняя плотность вероятности в данном прямоугольнике равна отношению вероятности (Р к площади прямоугольника АхАу, т. е.

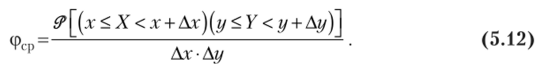
Будем неограниченно уменьшать стороны прямоугольника, т. е. Ах—>0, Аг/ —>0. Тогда, учитывая (5.11), найдем.

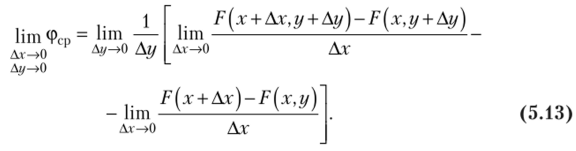
Так как функция F (x, у) непрерывна и дифференцируема по каждому аргументу, то выражение (5.13) примет вид.

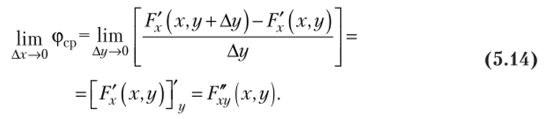
Онределе н и е. Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X, Y) называется вторая смешанная частная производная ее функции распределения, т. е.

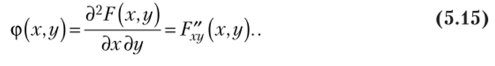
Геометрически плотность вероятности двумерной случайной величины {X, Y) представляет собой поверхность распределения в пространстве Oxyz (рис. 5.3).

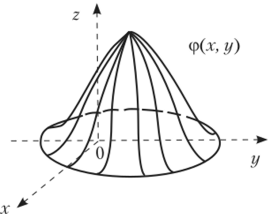
Рис. 5.3.

Плотность вероятности (р [х, у) обладает свойствами, аналогичными свойствам плотности вероятности одномерной случайной величины.

1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т. е.

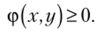
? Свойство вытекает из определения плотности вероятности как предела отношения (5.13) двух неотрицательных величин, ибо функция распределения f (x, у) — неубывающая функция по каждому аргументу. ?

2. Вероятность попадания непрерывной двумерной величины (X, У) в область О равна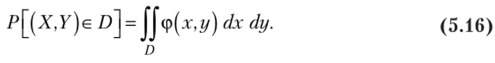

? Поясним геометрически формулу (5.16).

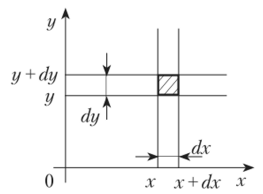
Рис. 5.4.

Подобно тому, как в гл. 4 для одномерной случайной величины X введено понятие «элемент вероятности», равный ц>(х)йх, для двумерной случайной величины (X, У) вводится также понятие «элемент вероятности», равный ф (.г, у)(1х ?у.Он представляет (с точностью до бесконечно малых более высоких порядков) вероятность попадания случайной точки (Х, У) в элементарный прямоугольник со сторонами с1х и ду (рис. 5.4).

Эта вероятность приближенно равна объему элементарного параллелепипеда с высотой ср (л, у), опирающегося на элементарный прямоугольник со сторонами (Ьс и ?у.

Если вероятность попадания одномерной случайной величины на отрезок [а, Ь] геометрически выражалась площадью фигуры, ограниченной сверху кривой распределения ф (х) и опирающейся на отрезок [а, Ь, и аналитически выражалась интегралом ф (х) сЬс, то вероятность попадания

3 а

двумерной случайной величины в область О на плоскости Оху геометрически изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения ф (х, у) и опирающегося на область О, а аналитически — двойным интегралом (5.16). ?

3. Функция распределения непрерывной двумерной случайной величины может быть выражена через ее плотность вероятности ф (х, у) по формуле

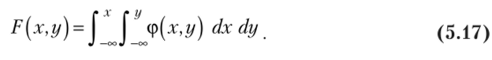
? Функция распределения Е (х, у) есть вероятность попадания в бесконечный квадрант Д который можно рассматривать как прямоугольник, ограниченный абсциссамиаз и х и ординатамиоо и у. Поэтому в соответствии с формулой (5.16).

?

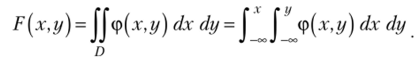4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице'.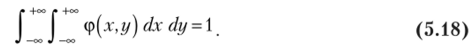

? Несобственный интеграл (5.18) есть вероятность попадания во всю плоскость Оху, т. е. вероятность достоверного события, равная 1. Это означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью Оху, равен 1. ?

Зная плотность вероятности двумерной случайной величины (X, К), можно найти функции распределения и плотности вероятностей ее одномерных составляющих X и У.

Так как в соответствии с равенствами (5.9) Р[х, +оо) = Р_{(х) и Т (+оо, у) = Р₂(у), то, взяв в формулах (5.17) соответственно у = +оо и х = +оо, получим функции распределения одномерных случайных величин X и У:

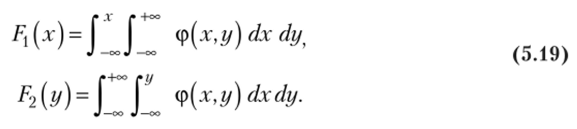
Дифференцируя функции распределения ЕДх) и Р₂{у) соответственно по аргументам х и у, получим плотности вероятности одномерных случайных величин X и У:

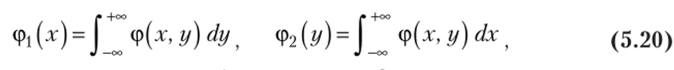
т.е. несобственный интеграл в бесконечных пределах от совместной плотности ф (х, у) двумерной случайной величины по аргументу х дает плотность вероятности (р₂(г/), а по аргументу у — плотность вероятности срДх).

Замечание. Если имеется кривая распределения ф (х) одномерной случайной величины X, то конкретное значение ее плотности вероятности в данной точке х определяется геометрически о р д и н, а т о й кривой ф (.г). Если имеется поверхность распределения ф (х, у) двумерной случайной величины (X, У), то конкретное значение ее совместной плотности в данной точке (х, у) определяется геометрически аппликатой поверхности ф (х, у). В этом случае конкретное значение плотности вероятности фдх) одномерной составляющей X в данной точке х, в соответствии с формулой (5.20), определится геометрически площадью сечения поверхности ф (х, у) плоскостью X = х, параллельной координатной плоскости Оуг и отсекающей на оси Ох отрезок х. Аналогично конкретное значение плотности ф₂(у) одномерной составляющей У в данной точке у есть площадь сечения поверхности ф (х, у) плоскостью У = у, параллельной координатной плоскости Охг и отсекающей на оси Оу отрезок у (см. рис. 5.9, на котором значение ф₂ {у) при данном у представляет площадь сечения, равную 5).

[> Пример 5.3. Двумерная случайная величина распределена равномерно в круге радиуса Я = 1 (рис. 5.5). Определить: а) выражение совместной плотности и функции распределения двумерной случайной величины (Х, У); б) плотности вероятности и функции распределения одномерных составляющих X и К; в) вероятность того, что расстояние от точки (Х, У) до начала координат будет меньше 1/3.

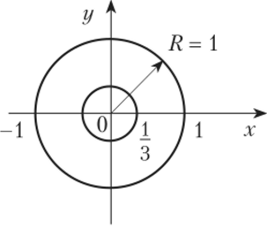
Рис. 5.5.

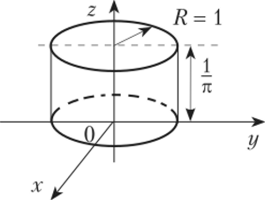
Рис. 5.6.

х С при х² + у²< 1,.

Решение, а) По условию Ф [х, у) = _Л 0

^{4 7} [0 при х²+у²> 1.

Постоянную С можно найти из соотношения (5.18):

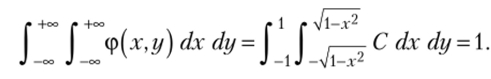
Проще это сделать, исходя из геометрического смысла соотношения (5.18), означающего, что объем тела, ограниченного поверхностью распределения ф (дг, у) и плоскостью Оху у равен 1. В данном случае это объем цилиндра с площадью основания л/?² = к • I² = к и высотой С (рис. 5.6), равный п С = 1, откуда С = 1/л. Следовательно,.

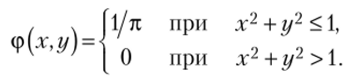
Найдем функцию распределения F[:г, г/) по формуле (5.17):

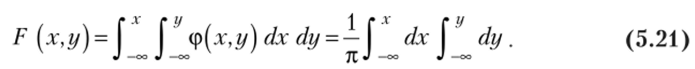
Очевидно, что этот интеграл с точностью до множителя /п совпадает с площадью области D — области пересечения круга о? + у² < 1 с бесконечным квадрантом левее и ниже точки М (х, у) (рис. 5.7).

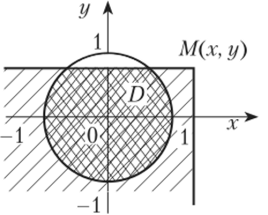
Рис. 5.7.

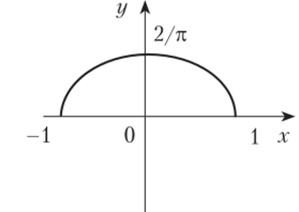
Рис. 5.8.

Опустим расчеты интеграла (5.21) для различных х и г/, предоставив их читателю, но отметим очевидное, что при х < -1, -оо < у < +со или приоо < х < +оо, у < -1 Р (х_у у) = 0, так как в этом случае область Р) — пустая, а при х > 1, у > 1 Р (х, у) = 1, так как при этом область ?) полностью совпадает с кругом х² + у² < 1, на котором совместная плотность ср (х, у) отлична от нуля.

б) Найдем функции распределения одномерных составляющих X и У. По формуле (5.19) при -<�х< 1.

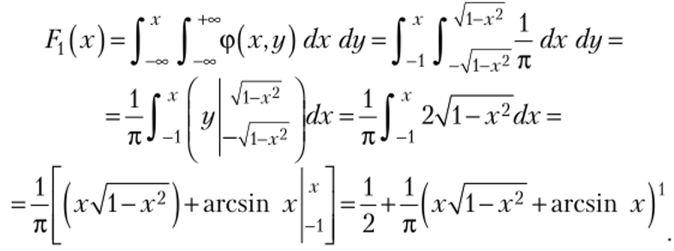
Итак,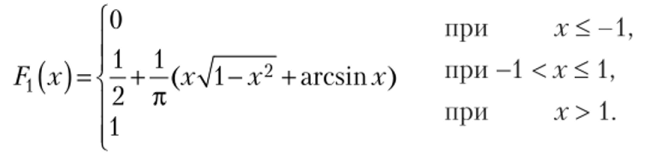

Аналогично.

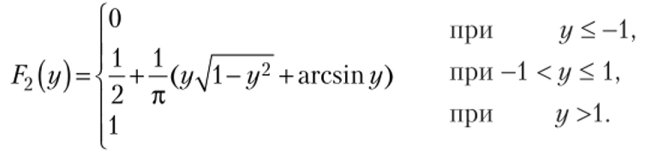
Найдем плотности вероятности одномерных составляющих X и У. По формуле (5.20).

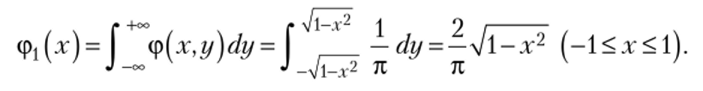
График плотности (рДх) показан на рис. 5.8.

Аналогично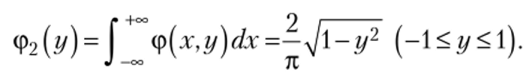

в) Искомую вероятность 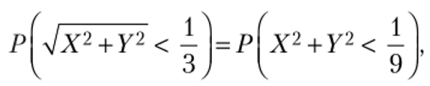т.с. вероятность того, что случайная точка (Х_уУ) будет находиться в круге радиуса.

= 1/3 (см. рис. 5.5), можно было найти по формуле (5.16):^[1]

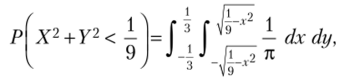aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">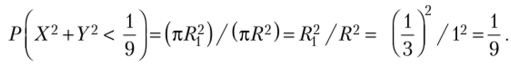

но проще это сделать, используя понятие «геометрическая вероятность», т. е.

• [1] Можно сказать, что для функциипервообразная есть