Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)

Пусть генеральные совокупности Хн Y распределены нормально, причем их дисперсии неизвестны. Например, по выборкам малого объема нельзя получить хорошие оценки генеральных дисперсий. По этой причине метод сравнения средних, изложенный в § 11, применить нельзя.

Однако если дополнительно предположить, что неизвестные генеральные дисперсии равны между собой, то можно построить критерий (Стьюдента) сравнения средних. Например, если сравниваются средние размеры двух партий деталей, изготовленных на одном и том же станке, то естественно допустить, что дисперсии контролируемых размеров одинаковы.

Если же нет оснований считать дисперсии одинаковыми, то, прежде чем сравнивать средние, следует, пользуясь критерием Фишера — Снедекора (см. § 8), предварительно проверить гипотезу о равенстве генеральных дисперсий.

Итак, в предположении, что генеральные дисперсии одинаковы, требуется проверить нулевую гипотезу Я₀: М (Х) = М (У). Другими словами, требуется установить, значимо или незначимо различаются выборочные средние хну, найденные по независимым малым выборкам объемов п и т.

В качестве критерия проверки нулевой гипотезы примем случайную величину.

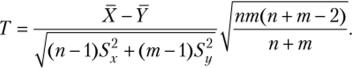
Доказано, что величина Тпри справедливости нулевой гипотезы имеет^{распределение} Стьюдента с k-n + m — 2 степенями свободы.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай. Нулевая гипотеза Я₀: М (Х) = М{ Y). Конкурирующая гипотеза Я: М (Х) ф М (У).

В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия Тв эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости а.

Наибольшая мощность критерия (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда «левая» и «правая» критические точки выбраны так, что вероятность попадания критерия в каждый из двух интервалов двусторонней критической области равна а/2:

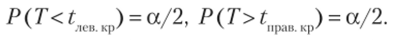
Поскольку величина Т имеет распределение Стыодента, а оно симметрично относительно нуля, то и критические точки симметричны относительно нуля. Таким образом, если обозначить правую границу двусторонней критической области через ?_двуст ^(a; к), то левая граница равна -?_двуст._кр(ос; k). Итак, достаточно найти правую границу двусторонней критической области, чтобы найти саму двустороннюю критическую область: Т < -t_ABycTKf>(), Т > > ?двуст.к,>(а; к)^и область принятия нулевой гипотезы: [~t_{aByCT Kp}(a; k),.

^двуст. кр (^> ^0]*.

Обозначим значение критерия, вычисленное по данным наблюдений, через Г_набл и сформулируем правило проверки нулевой гипотезы.

Правило 1. Для того чтобы при заданном уровне значимости, а проверить нулевую гипотезу Н₀: М (Х) = М (Y) о равенстве математических ожиданий двух нормальных совокупностей с неизвестными, но одинаковыми дисперсиями (в случае независимых малых выборок) при конкурирующей гипотезе Н_х: М (Х) Ф М (У), надо вычислить наблюдаемое значение критерия:

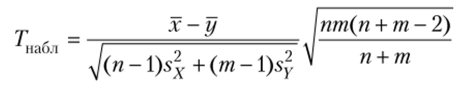
и по таблице критических точек распределения Стыодента, по заданному уровню значимости, а (помещенному в верхней строке таблицы) и числу степеней свободы к — п + m — 2 найти критическую ТОЧКУ Свуст. кр (^а*> к).

Если | Г_набл | < ?_{двуст кр}(а; к) — отвергнуть нулевую гипотезу нет оснований.

Если | Г_набл | > ?д_Вуст.кр (а; к) — нулевую гипотезу отвергают, Пример. Но двум независимым малым выборкам, объемы которых соответственно равны п = 5иш = 6, извлеченным из нормальных генеральных совокупностей X и У, найдены выборочные средние х = 3,3, у = 2,48 и исправленные дисперсии s =0,25 и Sy =0,108. При уровне значимости 0,05 проверить нулевую гипотезу Н₀: М (Х) = М ( У) при конкурирующей гипотезе //: М (Х) ф Щ У).

Р е ш е н и е. Так как выборочные дисперсии различны, проверим предварительно нулевую гипотезу о равенстве генеральных дисперсий, пользуясь критерием Фишера — Снедекора (см. § 8).

Найдем отношение большей исправленной дисперсии к меньшей:

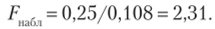
Дисперсия л’у значительно больше дисперсии Sy, поэтому в качестве конкурирующей примем гипотезу Н_{: D (X) > D (Y). В этом случае критическая область — правосторонняя. По таблице, но уровню значимости, а = 0,05 и числам степеней свободы &, = 5 — 1 = 4, k₂ = 6−1 = 5 находим критическую точку F ,(0,05; 4; 5) = 5,19.

Так как F_iafci < F — нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий.

Поскольку предположение о равенстве генеральных дисперсий выполняется, сравним средние.

Вычислим наблюдаемое значение критерия Стьюдента:

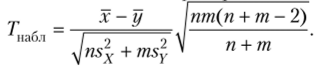
Подставив числовые значения величин, входящих в эту формулу, получим Г_ю6л = 3,27.

По условию, конкурирующая гипотеза имеет вид М (Х) ф М (У), поэтому критическая область — двусторонняя. По уровню значимости 0,05 и числу степеней свободы & = 5 + 6- 2 = 9 находим по таблице (см. приложение 6) критическую точку t (0,05; 9) = 2,26.

Так как Т, > t — нулевую гипотезу о равенстве генеральных набл двуст. кр ^{J J} j t t.

средних отвергаем. Другими словами, выборочные средние различаются значимо.

Второй случай. Нулевая гипотезаЯ₍₎: М (Х) = M (Y). Конкурирующая гипотеза Н_{ М (Х) > М ( У).

В этом случае строят правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия Т в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:

Критическую точку f_np_aiM)CI,_Kp(ot; k) находят по таблице приложения 6, по уровню значимости а, помещенному в нижней строке таблицы, и по числу степеней свободы k = п + m - 2.

Если ГнабдС^правост.кр^— нет оснований отвергнуть нулевую гипотезу.

Если Г_набл > ^"равост._Кр^— нулевую гипотезу отвергают.

Третий случай. Нулевая гипотезаЯ₀: М (Х) -M (Y). Конкурирующая гипотезаН_{: М{Х) <�М (У).

В этом случае строят левостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:

В силу симметрии распределения Стьюдента относительно нуля^{левост.кр} = —бфавост. к_Р— Поэтому сначала находят «вспомогательную» критическую точку ,_г так, как описано во втор о м с л у ч, а е, И ПОЛаГаЮТ ь_лсвост. кр^{правост.} кр*.

Если Г_набл > - ?_11равост.кр— отвергнуть нулевую гипотезу нет оснований.

Если Т_{т ()Л} < — ^_{правосх}._кр — нулевую гипотезу отвергают.