Непрерывный спектр стационарной случайной функции. 
Спектральная плотность

Среди стационарных случайных функций есть такие функции, корреляционные функции которых нельзя представить в виде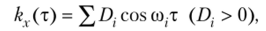

где число слагаемых конечно или счетно. Спектр этих функций не дискретный, а непрерывный. Для рассмотрения стационарных случайных функций с непрерывным спектром необходимо ввести понятие спектральной плотности.

Выше, когда частоты гармоник спектрального разложения стационарной случайной функции были дискретными и равноотстоящими, был получен дискретный линейчатый спектр, причем соседние частоты отличались на величину Дсо = %/Т. Пусть Г—>, тогда Дш —> 0. Ясно, что при этом частота изменяется непрерывно (поэтому обозначим ее через со без индекса), соседние ординаты спектра сближаются и в пределе вместо дискретного спектра мы получим непрерывный спектр, т. е. каждой частоте со (со > 0) соответствует ордината, которую обозначим через s* (со).

Хотя отрицательные частоты физического смысла не имеют, для упрощения вычислений целесообразно считать, что частоты изменяются в интервале (-(c)о, оо), и вместо функции s*(co) рассматривать функцию, которая имеет вдвое меньшие ординаты:

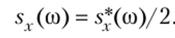
Спектральной плотностью стационарной случайной функции X (t) называют функцию s_x(co), которая связана с корреляционной функцией k/x) взаимно обратными преобразованиями Фурье:

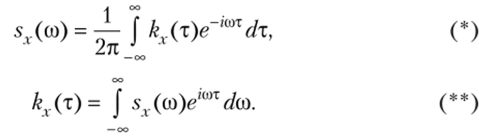
Эти формулы называют формулами Винера — Хинчина. В действительной форме они представляют собой взаимно обратные косинус-преобразования Фурье:

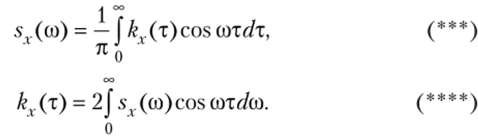
Важное значение спектральной плотности состоит в том, что, зная ее, можно найти корреляционную функцию, и обратно (в этом смысле спектральная плотность и корреляционная функция эквивалентны); кроме того, как уже было указано, использование спектральной плотности в ряде случаев значительно упрощает теоретические и практические расчеты.

Подчеркнем, что, как следует из формулы (***), спектральная плотность — четная функция:

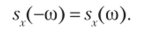
Выясним вероятностный смысл функции s_r(co). Положив т = О в соотношении (****) и учитывая, что k_r(0) = D_v, s_v(co) — четная функция, получим.

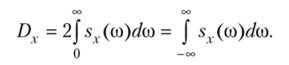
Видим, что дисперсия стационарной случайной функции X (t) представляет собой «сумму» элементарных дисперсий s_v( со) dco — = s_v(co)Aco; каждая элементарная дисперсия соответствует частичному интервалу частот Дсо. В частности, частичному интервалу Дсо = со. — со соответствует дисперсия.

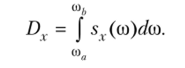
По теореме о среднем, 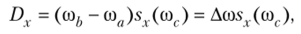где со <<�в <<�о,.

а с 1>

Отсюда.

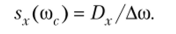
Из этой формулы заключаем:

• а) величину х_г(со,) можно истолковать как среднюю плотность дисперсии на частичном интервале Доз, содержащем частоту со;
• б) при Дсо —> 0 естественно считать, что х_л.(со) — плотность дисперсии в точке со_г. Поскольку никаких ограничений на частоту со наложено не было, полученный результат справедлив для любой частоты.

Итак, спектральная плотность описывает распределение дисперсий стационарной случайной функции по непрерывно изменяющейся частоте.

Из вероятностного смысла спектральной функции следует, что спектральная плотность — неотрицательная функция 5_г(ю)>0.

Пример 1. Найти спектральную плотность стационарной случайной функции X (t), зная ее корреляционную функцию.

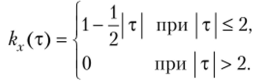
Р е ш е н и e. Используя формулу 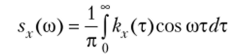и учитывая, что | т | = т в интервале (0,2), имеем.

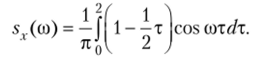
Интегрируя по частям, окончательно получим искомую спектральную плотность:

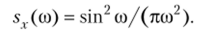
Пример 2. Найти спектральную плотность стационарной случайной функции X (t), зная ее корреляционную функцию k_r(x) = De¹¹, а > 0.

Решение. Используем формулу

Учитывая, что | т | = —т при т 0, получим 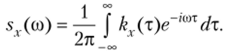Следовательно,

Выполнив интегрирование, найдем искомую спектральную плотность:

Пример 3. Найти корреляционную функцию стационарной случайной функции X (t), зная ее спектральную плотность

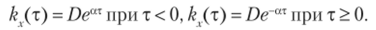
Решение. Используя формулу.

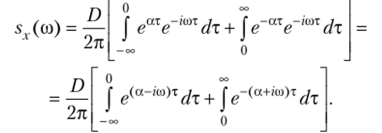
и учитывая, что s (со) = со₀ в интервале (0, оо₀), имеем.

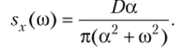
Выполнив интегрирование, получим искомую корреляционную функцию: