Интегральная функция распределения

Для количественного описания распределения вероятностей удобно воспользоваться не вероятностью события X = х, а вероятностью события X < х, где х — некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х и является некоторой функцией от х. Эта функция называется функция распределения случайной величины X и обозначается F (x):

Функцию F (x) иногда называют интегральной функцией распределения, или интегральным законом распределения.

Функция распределения — самая универсальная характеристика СВ. Она существует как для дискретных, так и непрерывных СВ. Функция распределения полностью характеризует СВ с вероятностной точки зрения и является одной из форм закона распределения.

Общие свойства интегральной функции распределения:

• 1. Функция распределения F (x) неубывающая функция своего аргумента, то есть при х₂ > х, F (x₂) > /^г(х₁).
• 2. На минус бесконечности функция распределения равна нулю: F (-oo) = 0.
• 3. На плюс бесконечности функция распределения равна единице: F (+oo) = l.
• 4. P (x,₂) = F (x₂)-F (x₁).

График функции распределения в общем случае представляет собой график неубывающей функции, значение которой начинается от 0 и доходит до 1, причем в отдельных точках функция может иметь разрыв.

Зная ряд распределения дискретной СВ, можно легко построить функцию распределения этой величины. Действительно:

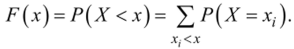
ПРИМЕР 2. Произведем один опыт, в котором может произойти или не произойти событие Л. Вероятность события А равна р = 0,3. СВ X — число появлений события А в опыте (дискретная СВ). Необходимо построить функцию распределения СВ.

РЕШЕНИЕ. Ряд распределения СВ X имеет вид:

Построим функцию распределения СВ Л" :

• 1) при х<0 F (x)=P (X <�х)=0;
• 2) при 0 < х<1 Е (х) = Р (Х <�х) = Р (Х = 0) = 0,7;
• 3) при х> 1 F (x) = P (X <�х) = Р (Х = 0) + Р (Х = 1) = 1.

ПРИМЕР 3. При тех же условиях (ПРИМЕР 2) провели 4 независимых опыта. Постройте функцию распределения числа появлений события А.

РЕШЕНИЕ. Пусть СВ X — число появлений события А в 4 опытах. Эта величина имеет ряд распределения:

Построим функцию распределения СВ X:

Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось {либо отрезок {отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.

Для непрерывной случайной величины вероятность попасть на интервал равна.

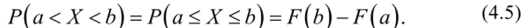
Пусть имеется непрерывная СВ X с функцией распределения F{x), которую мы предполагаем непрерывной и дифференцируемой. Вычислим вероятность попадания этой СВ на участок от х до х + Дх, то есть приращение функции распределения на этом участке:

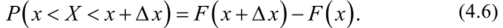
Найдем отношение этой вероятности к длине участка, то есть среднюю вероятность, приходящуюся на единицу длины на этом участке, и устремим Дх к 0. В пределе получим производную функции распределения'.

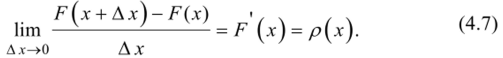
Функция р{х) — производная функции распределения, характеризует плотность, с которой распределяются значения СВ в данной точке.

Эта функция называется плотностью распределения {иначе — «плотностью вероятности») непрерывной СВ X.

Плотность распределения является одной из форм закона распределения. Эта форма не является универсальной, так как р (х) существует только для непрерывных СВ.

Рассмотрим непрерывную СВ X с плотностью распределения р (х) и элементарный участок dx, примыкающий к точке х.

Вероятность попадания СВ I на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна /?(х)г/х. Геометрически — это площадь элементарного прямоугольника, опирающегося на отрезок dx (рис. 4.2).

Выразим вероятность попадания СВ X на отрезок от а до [5 через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем участке, то есть интегралу: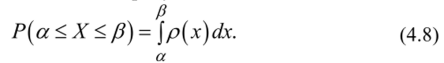

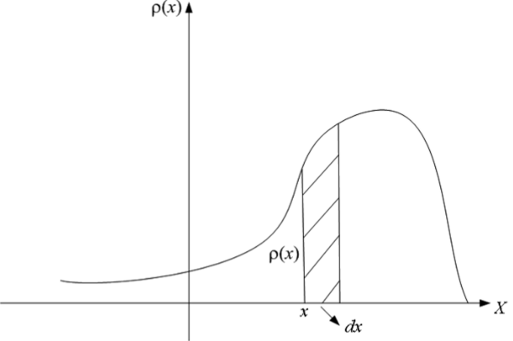
Рис. 4.2. Вероятность попадания на элементарный интервал

Геометрически вероятность попадания величины X на отрезок [а, р равна площади фигуры, ограниченной кривой распределения и опирающейся на этот участок (рис. 4.3).

Формула (4.7) выражает плотность распределения СВ через интегральную функцию распределения. Поставим обратную задачу — выразим функцию распределения через плотность. Согласно определению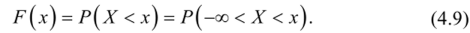

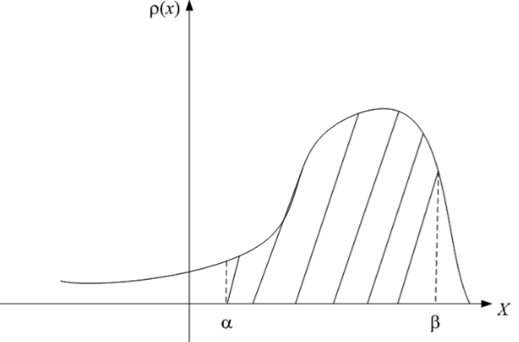
Рис. 4.3. Вероятность попадания на интервал

Из формулы (4.9) с учетом (4.8) получим:

Геометрически F (x) есть не что иное, как площадь фигуры, ограниченной плотностью распределения (сверху) и осью абсцисс (снизу) и лежащей левее точки х (рис. 4.4).^[1][2]

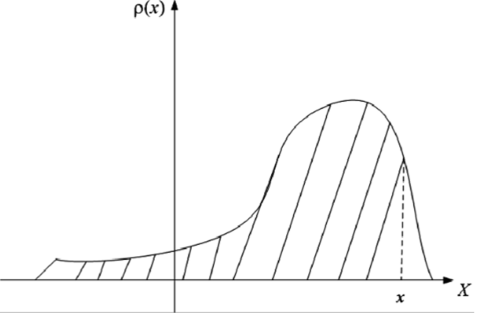
Рис. 4.4. Вычисление функции распределения через плотность СВ.

Основные свойства плотности распределения

Рассмотрим несколько примеров.

ПРИМЕР 4. Функция распределения непрерывной СВ X равна.

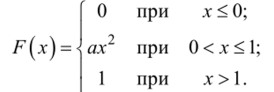
Необходимо найти: коэффициент д, плотность распределения /(х), и, наконец, вероятность />(0,25 < х < 0,5).

РЕШЕНИЕ:

a) Так как F (x) — функция непрерывная, то при х = 1, ах² = а х I = 1, то есть а = 1;

0 при х < 0;

b) /(х) = F (х) = < 2х при 0 < х < 1;

0 при х>1;

c) /^>(0,25^r(0,5)-F (0,25) = 0,25−0,0625 = 0,1875. ПРИМЕР 5. СВ X подчинена закону распределения с плотностью.

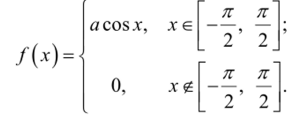
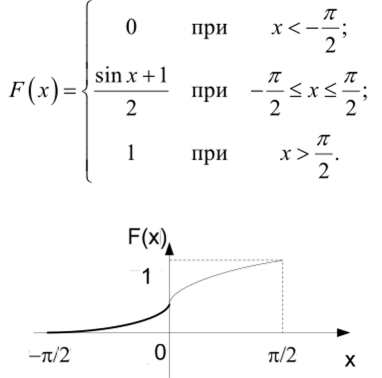
Необходимо: а) найти коэффициент д, Ь) построить график плотности распределения ./ (х), с) найти F (x) и построить график, d) найти ве;

7Г

роягность попадания СВ X на участок [0, —].

РЕШЕНИЕ:

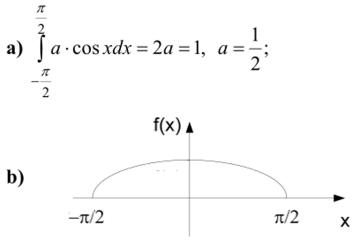
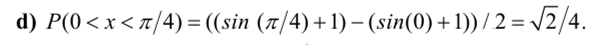
• [1] Плотность распределения является неотрицательной функцией Эго свойство непосредственно вытекает из того, что функция распределения F (x) — неубывающая.
• [2] Интеграл в бесконечных пределах от плотности распределенияравен единице. Действительно, Геометрически основные свойства плотности распределения означают: • кривая распределения лежит не ниже оси абсцисс; • площадь фигуры, ограниченной кривой распределения и осьюабсцисс, равна единице.