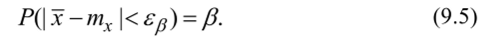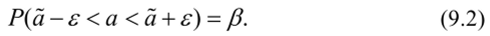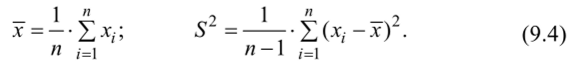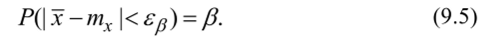Интервальное оценивание. 
Теория вероятностей и математическая статистика

Ранее мы обсудили использование выборочных значений в качестве оценок параметров случайных величин. Однако такие процедуры дают только точечные оценки интересующих нас параметров и не позволяют судить о степени близости выборочных значений к оцениваемому параметру. Более предпочтительная процедура — построения интервала, который накрывает оцениваемый параметр с известной степенью достоверности. Такой подход называется «интервальным оцениванием». Сразу отмстим следующее: чем больше уверенность в том, что оцениваемый параметр лежит в интервале, тем шире интервал. Так что искать интервал, накрывающий параметр с вероятностью, равной единице, бессмысленно. Это вся область 0 с R, то есть I = (-оо, + оо).

Пусть для параметра а получена несмещенная оценка а. Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность (3 (например: >3 = 0,9; 0,95; …), такую, что событие с вероятностью (3 можно считать практически достоверным, и найдем такое значение е, для которого выполняется соотношение.

Тогда диапазон практически возможных значений ошибки, возникающей при замене а на а, будет равен ±е. Ошибки, большие по абсолютной величине е, будут появляться с малой вероятностью а = 1 — (3. Запишем (9.1) в другом виде:

То сеть неизвестное значение параметра а с вероятностью (3 попадает в интервал.

Ранее (в теории вероятностей) мы рассматривали вероятность попадания случайной величины на некоторый интервал. У нас же а не случайная величина, а интервал случаен, здесь корректно говорить о вероятности 1р накрыть точку а.

Вероятность [3 принято называть доверительной вероятностью, а интервал 1р — доверительным интервалом.

Рассмотрим задачу нахождения доверительных границ а, и а₂ параметра а, имеющего несмещенную оценку а. Если бы нам был известен закон распределения величины а, то из выражения (9.1) нахожденис е при заданной /? нс представляло бы затруднений. Однако, как правило, мы не знаем закон распределения случайной величины X.

Пусть теперь распределение случайной величины X отлично от нормального. Применяя центральную предельную теорему, получаем следующий результат.

С увеличением объема выборки п выборочное распределение выборочного среднего х стремится к нормальному распределению независимо от вида распределения исходной случайной величины.

Практически во многих случаях выборочное х можно считать нормальным уже при п > 4, а при п > 10 приближение будет хорошим.

В качестве примера рассмотрим задачу нахождения доверительного интервала математического ожидания. Пусть произведено п независимых опытов над случайной величиной X с неизвестными m_x, D_x. Для этих параметров выберем оценки:

Необходимо построить доверительный интервал 1р, соответствующий доверительной вероятности /?: