Параллельное соединение. 
Основы теории цепей

На рис. 6.4 показано параллельное соединение двух НЭ, характеристики которых представлены на рис. 6.5. Эти два НЭ могут быть заменены одним с характеристикой /({/), изображенной пунктирной линией.

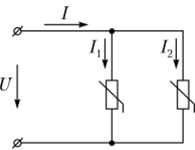
Рис. 6.4. Параллельное соединение двух нелинейных элементов

Рис. 6.5. Расчет токов в параллельной электрической цепи.

Для этого, задаваясь произвольными значениями напряжения, суммируют соответствующие ординаты характеристик, заданных для НЭ.

Аналогично может быть построена результирующая характеристика цепи при параллельном соединении нескольких НЭ.

Смешанное соединение

Смешанное соединение трех НЭ показано на рис. 6.6, а. После замены двух параллельно соединенных НЭ одним эквивалентным схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух НЭ. Графическое построение для определения токов и напряжений приведено на рис. 6.6, 6.

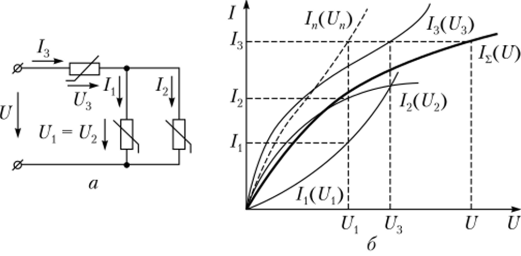
Рис. 6.6. Смешанное соединение нелинейных элементов:

а — схема цепи; б — расчет токов Сначала характеристики I{U) и /₂(/У₂) заменяют одной I_n(U_n), суммируя токи для нескольких значений напряжений, а затем по полученной характеристике и заданной ?/₃(/з) строят суммарную ВАХ цепи /_s(t/), суммируя напряжения для нескольких значений токов.

Для любого значения U но суммарной ВАХ I^(U) можно определить ток /₃ и напряжения на параллельном участке цени U> и напряжение на нелинейном элементе Щ.

Зная напряжение U, можно определить токи 1 и /₂ по ВАХ I (U) и /₂(U₂).

Пример 6.1.

Для стабилизации тока в цепи с сопротивлением нагрузки R = 30 Ом применен бареттер, вольт-амперная характеристика которого показана на рис. 6.7. Требуется определить возможные пределы изменения приложенного к цепи ЭДС, при которых ток в цепи будет изменяться от 0,25 до 0,3 А.

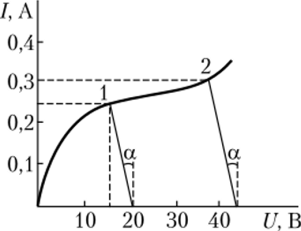
Рис. 6.7. График к примеру 6.1

На характеристике бареттера находим токи, которые соответствуют заданным пределам изменения (точки 1 и 2).

Через эти точки проводятся прямые, соответствующие уравнениям U = = Е— IR. Для точки 1 U = 12,5 В, 1 = 0,25 А, тогда Е = U + IR = 20 В. В точке 2 U2 = 36 В, /₂ = 0,3 А, тогда Е₂ = 45 В.

Расчет нелинейной цепи методом двух узлов

Необходимо определить напряжение U между узлами b и а, при котором сумма токов в узле равна нулю ц + i₂ + ц = 0.

Для этого установим зависимость напряжения U от токов в соответствующей ветви (или соответствие токов от U)

Чтобы построить эти зависимости, нужно графики U (I) и f/₃(/₃) сместить влево на величину -Е и -?₃ соответственно, а график U₂(I₂) оставить на месте (без изменений).

Суммируя эти графики, получаем зависимость напряжения U от суммарного тока (пунктир на рис. 6.8, в). Так как сумма токов в узле равна.

Рис. 6.8. Расчет цепи методом двух узлов:

а — схема цепи; б — заданные ВАХ элементов; в — расчет токов нулю, то там, где эта кривая пересекает ось абсцисс, находим искомое напряжение U (при котором сумма токов в узле равна нулю). Проведем через это напряжение вертикальную линию до пересечения с построенными ранее кривыми (смещенными на Е и ?3). Точки пересечения этой вертикальной линии с кривыми определят точки /_ь /₂ и /3.