Понятие об алгоритмах и сложности вычислений

Алгоритм относится к важнейшим понятиям как в математике в целом, так и в теории сложности вычислений. Вычислительный алгоритм (не строго) — это правило, данное на некотором языке и определяющее последовательность действий для решения поставленной задачи с использованием исходных данных. Алгоритм должен быть понятным для исполнителя, определенным (все действия должны трактоваться однозначно) и массовым, т. е. применимым к определенному множеству исходных данных. Важность алгоритмов проявляется в различных аспектах. При решении задач алгоритмы являются: формой изложения научных результатов, руководством к действию, средством экономии умственного труда, необходимой компонентой автоматизации, инструментом анализа и решения, элементами доказательной базы математики, средством описания сложных объектов и процессов в науке.

Любой вычислительный алгоритм А отображает исходные (или входные) данные х в выходные данные у, иначе говоря, Л реализует для некоторой функции f:X—>Y и для некоторого х е X вычисление у = /(х). Реализация алгоритма, А на входных данных х описывается характеристиками сложности: числом шагов алгоритма; числом оговоренных вычислительных операций, например числом умножений и сложений чисел некоторого поля;

временем выполнения и объемом используемой памяти вычислительного устройства и др. Точное описание характеристик сложности как функций от х является, как правило, проблематичным, поэтому при анализе сложности алгоритмов обычно рассматривают оценочные характеристики.

Наиболее распространен подход к оценке сложности алгоритмов, основанный на установлении количественной зависимости характеристик сложности от размера п входных данных, п е N. Характеристики сложности изучаются как функции от п, соответствующие «худшему случаю» (максимуму по х) или среднему случаю, когда на множестве значений х определена некоторая вероятностная мера.

Пусть входные данные алгоритмов представляются словами в некотором алфавите. Алгоритм называется полиномиальным {имеющим полиномиальную сложность), если существует действительный полином р (Х) с положительными коэффициентами такой, что для любого натурального п время работы алгоритма на любом входном слове длины п не превосходит р (п). Класс задач называется полиномиальным, если любая задача из данного класса может быть решена полиномиальным алгоритмом. Заметим, что речь идет о бесконечных классах, так как п е N. Через Р обозначим класс всех полиномиальных задач. К Р относятся, например, задачи решения систем линейных уравнений, обращения матриц и др.

Для распознавания полиномиальности данного класса задач не обязательно находить полином р{Х). Теория сложности вычислений использует в ряде случаев технику математических доказательств, позволяющую установить полиномиальность одного класса задач с помощью сводимости к задачам другого класса, полиномиальность которых уже доказана. Вместе с тем для большинства практических задач не известно, входят ли они в класс Р. Часто такие задачи оказываются в другом классе более сложных задач, обозначаемом NP. К NP относятся, например, задачи распознавания в графе наличия клики заданного размера, гамильтонова цикла и др.

Сложность неполиномиальных задач обычно характеризуется экспоненциальными и субэкспоненциальными оценками, последние занимают промежуточное положение по сложности между полиномиальными и экспоненциальными оценками [4, 9J.

При анализе сложности вычислительной задачи важным является представление чисел. Числа 0,…, b — 1 называют цифрами по основанию Ь. Разложение числа пе N₀no основанию {базе) b есть набор {d_k__x,…, d_x, d₍₎)_h чисел из N₀, где di е{0, b — 1}, i = 0, 1, …, k — 1, и п = {d_k_ _1? …, d_{, d₀)_h п = = d_k__xb^k~^x + … + d_xb + d₀.

Если d_k__x > 0, то число п называют k-разрядным b-ичным числом. Любое целое от Ь^к~^х до Ь^к — 1 является^{-разрядным} 6-ичным числом. Число разрядов k определяется для п выражением.

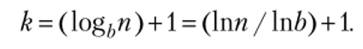
При записи числа п в виде {d_k__ifd_x, d₀)_b скобки и индекс (…)/, обычно опускают в случае b = 10 или когда основание системы счисления ясно из контекста.

Рациональные числа также можно разлагать по любому основанию, т. е. представлять в виде (d_k__1? …, d_v d₀> d__{1 d_₂, …, d_i)_h. При b > 10 принято использовать буквы некоторых алфавитов для обозначения цифр по основанию Ь. Например, при b — 16 используем буквы A—F латинского алфавита для записи цифр 10—15 соответственно.

При вычислениях используются различные системы счисления и переходы от одного основания к другому.

Пример 1.8.

• а) умножить 160 на 199 в 7-ичной системе счисления. Определим: 160 = (316)₇, 199 = (403)₇. Умножение «в столбик» дает результат 161 554;
• б) определить представления: (11 001 001)₂ = 201; (BAD)₂₆ = 679; (В, AD)₂₆ = 1—.
• 676

При вычислении дробных чисел сначала представляется целая часть. Затем дробная часть умножается на основание Ь. Целая часть результата дает d__v далее (умножая на Ь…) находим d_₂ и т. д.;

в) выразить 10⁶ в системах счисления, но основаниям 2, 7 и 26. Для разложения п но основанию Ь сначала получаем младший разряд как остаток от деления п на Ь. Потом частное от деления вновь делим на b и получаем следующий разряд и т. д. Результаты: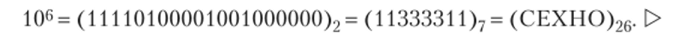

Иногда для записи чисел применяются смешанные системы счисления, использующие различные основания b_k__v Ь_к_₂,Ь₀. Например, если число п < < b_k__xb_k_₂…bо, то его можно представить в виде п = (d_k__vd_k_₂,…, d§)_bk x bk_₂ ^

это означает, что п = d_k__xc_k__x + … + d_xc_x + d₀, где dе {0,…, b_t — 1}, c_i+x = 6₀.Д, i = 0,…, k — 1.

При реализации алгоритма важно оценить трудоемкость выполнения его основных операций над числами. К таким операциям относятся, как правило, умножение и сложение чисел; деление и вычитание сводятся к ним. Приведем известные оценки для^{-разрядных} двоичных чисел, которые чаще других чисел используются для представления данных в вычислительных системах. Элементарной операцией при оценке считаем сложение двух битов (слово «бит» возникло как сокращение от английского словосочетания «/лпагу digit»).

Суммирование^{-разрядных} двоичных чисел. Эта операция требует сложения для каждого разряда двух битов и сложения получившейся суммы со знаком переноса из предыдущего разряда. Выражение «а имеет порядок 0(п)» означает, что при п —> °° величина а оценивается как сп, где с — константа. Тогда трудоемкость сложения, обозначаемая t (+k), имеет порядок O (k) или O (logAz) (здесь и далее основание логарифма полагается равным 2).

Умножение^{-разрядного} двоичного числа на /-разрядное двоичное число, / < k. Умножение «в столбик» равносильно сложениям не более / копий^{-разрядного} двоичного числа, где копии записаны с определенным сдвигом. Пренебрегая операциями сдвига как менее сложными, получаем, что для трудоемкости умножения, обозначаемой d^xkj), верна оценка.

d^xk, /) ~ (/ - l)?<⁺)(&). Следовательно, умножение двух^{-разрядных} двоичных чисел (его трудоемкость обозначим ?<*)(?)) имеет порядок 0(к²) или 0(og²n). Заметим, что лучшая из известных оценок трудоемкости умножения (используется другой алгоритм умножения) имеет порядок 0(к • log# х х loglog&). Трудоемкость вычитания (деления) чисел по порядку величины та же, что и при сложении (при умножении).

Данные оценки позволяют определить сложность алгоритмов путем сведения шагов алгоритма к суммированию и умножению^{-разрядных} двоичных чисел.

Вместо «сложности вычисления» иногда используют как синоним термин «время вычисления», что некорректно при обсуждении сложности параллельных вычислений.