Решение телеграфных уравнений

.

Чтобы перейти к решению обыкновенных дифференциальных уравнений (вместо уравнений в частных производных), воспользуемся преобразованием Лапласа. Заменим мгновенные значения напряжений и токов их изображениями. Для этого умножим правую и левую части уравнений (5.1.3) на e~st и проинтегрируем, но t от 0 до со. В результате такой замены получим систему уравнений в операторной форме.

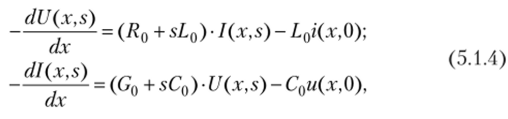
где i (x, 0), и (х, 0) определяют начальные условия, которые описывают распределение тока и напряжения вдоль линии при t = 0. В дальнейшем полагаем, что используются нулевые начальные условия, т. е. i (x, 0) = 0, и (х, 0) = 0.

Поскольку входящие в уравнения (5.1.4) неизвестные функции U (x, s) и I (x, s) зависят только от одной переменной (х), частные производные этих функций по х заменены полными (обыкновенными) производными.

Продифференцировав по х обе части первого уравнения.

(5.1.4), а затем подставив в него значение dl (x, s)/dx из второго уравнения, получим дифференциальное уравнение второго порядка относительно напряжения:

где введена величина у (5), которая называется операторным коэффициентом распространения:

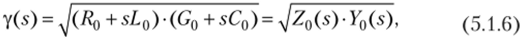
Z₀(s), Yq (s) — операторные погонное сопротивление и погонная проводимость линии.

Общее решение уравнения (5.1.5) имеет вид.

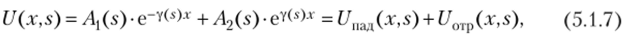
где ^(s), A₂(s) — постоянные интегрирования, определяемые граничными условиями, т. е. значениями неизвестных функций U (xу s) и I (x, s) в начале (х = 0) и (или) в конце (х = /) линии.

Подставляя (5.1.7) в первое уравнение (5.1.4) с учетом нулевых начальных условий и (5.1.6), найдем операторное изображение тока:

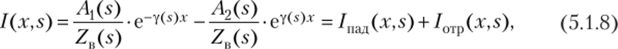
где величина Z"(s) называется операторным волновым сопротивлением, при этом.

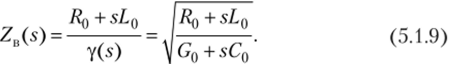
Постоянные интегрирования. Для определения A_{(s) и A₂(s) необходимо задать граничные условия, которыми служат напряжения и (или) токи в точках подключения к линии источника сигналов и нагрузки. Для их выбора можно использовать две величины из четырех возможных:

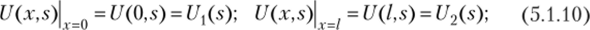
В табл. 5.1.1 приведено шесть возможных вариантов граничных условий, а также значения х, которые необходимо подставлять в соотношения (5.1.7), (5.1.8), чтобы получить систему уравнений для определения Aj (s) и Л₂(х).

Таблица 5.1.1

Вариант.	Граничные условия.	Подстановки x в уравнения (5.1.7), (5.1.8).
	lh (s)=U (0,5), 7,(5) = 7(0, 5).	x= 0 -> (5.1.7), д = 0 -" (5.1.8).
	U (s) = 77(0, s), 72(s) = 7(7, s)	дг= 0 —> (5.1.7),x= l-> (5.1.8).
	h (s) = 7(0, s), U2(s) = U (l, s)	x = 0 -> (5.1.8), л: = 7 -> (5.1.7).
	U2(s) = 77(7, .v), 72(s) = 7(7, s)	x = l-> (5.1.7), x = l-> (5.1.8).
	77, (s) = 77(0,5), 772(s) = 7/(7,5).	x= 0 -> (5.1.7), ДС = /(5.1.7).
	7,(s) = 7(0, s), 72(s) = 7(7, s)	л = 0 -> (5.1.8), я = 7 -> (5.1.8).

Если в качестве граничных условий выбраны напряжение и ток на конце линии, то после подстановки х — I в (5.1.7), (5.1.8) получим систему уравнений для определения постоянных интегрирования.

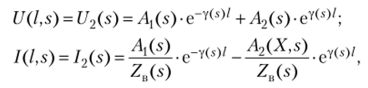
в результате решения которой находим.