Рассеяние в неупорядоченных системах

Рассеяние на случайном скоплении рассеивающих центров

Выше были рассмотрены основные закономерности явлений дифракции (рентгеновских лучей и других видов излучения) для случая регулярного расположения атомов в кристаллической решетке (положения атомов в решетке задаются трансляционным вектором r_;- = ah + Ыс + с О, благодаря чему эти явления выражены особенно отчетливо в виде интерференционной функции Лауэ и закона Брэгга. Естественно, что такая идеальная кристаллическая решетка — это крайний случай степени порядка. В реальном кристалле ситуация гораздо сложнее. Рассеивающие узлы (все или их часть) могут быть смещены из своего правильного положения в решетке, и тогда в направлениях интерференционных максимумов нарушится точное сложение амплитуд волн и их интенсивность для такой искаженной решетки ослабнет. Однако суммарная рассеянная энергия не должна уменьшаться, и поэтому в каких-то других направлениях, не отвечающих условиям дифракции, интенсивность рассеяния может увеличиваться. Таким образом, в результате нарушения правильного расположения рассеивающих центров происходит перераспределение интенсивности между дифракционными пиками и остальной частью обратного пространства. Иными словами, в случае рассеяния на реальном кристалле будет существовать заметное распределение диффузного рассеяния, в котором сосредоточена информация о нарушениях правильного расположения атомов в кристаллической решетке.

Наряду с кристаллическим состоянием вещества в природе широко распространены газообразное, жидкое и аморфное состояния. Поэтому естественно возникает вопрос, возможно ли использовать рассеяние излучений для получения информации о строении неупорядоченных или слабо упорядоченных систем [5].

Рассмотрим случай, когда атомы или другие рассеивающие частицы располагаются в пространстве произвольно, а координаты их могут быть описаны лишь на языке функций распределения вероятностей (имеются в виду случайные скопления рассеивающих частиц). Пусть рассеивающий объем состоит из N атомов, мгновенные положения которых заданы векторами г_ь г₂, …, г, …, r_N. Пусть также/_1;/₂,.

/дг — атомные множители рассеяния, соответствующие различным сортам N атомов, s₀, s — единичные векторы, определяющие направления падающего и дифрагированного пучков. Тогда, как и в случае идеальных кристаллов, можно записать суммарную мгновенную амплитуду рассеянного излучения в точке наблюдения М (см. рис. 1.6) в виде.

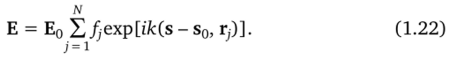
Полученное выражение можно переписать, воспользовавшись понятием обратного пространства и заменив /c (s — s₀) = Н, где Н — вектор обратного пространства. Тогда выражение (1.22) примет вид.

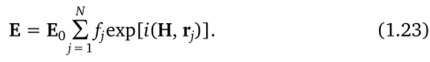
Суммирование производится по всем атомам рассеивающего объема. Чтобы получить выражение для интенсивности рассеяния, необходимо умножить рассеянную амплитуду на комплексно сопряженную. Для того чтобы учесть все члены суммы, следует умножать слагаемые с отличными индексами, т. е.

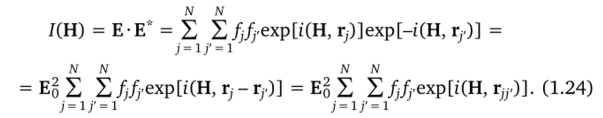
Здесь r_jy = Tj— Ту.

В некоторых случаях может быть полезным другое выражение для интенсивности рассеяния, которое может быть получено, если выделить в отдельный член все слагаемые с одинаковыми индексами, т. е.

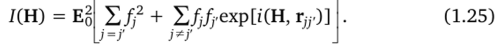
Таким образом, чтобы вычислить мгновенную интенсивность рассеяния, необходимо знать координаты всех рассеивающих частиц в любой момент времени. Эта информация для таких сложных систем, как газы, жидкости или аморфные материалы, не может быть получена, так как рассеивающие атомы в этих системах находятся в непрерывном движении. Поэтому имеется единственная возможность — определять среднее значение интенсивности рассеяния по времени. Усреднять придется фазовый множитель, стоящий под знаком суммы. Это возможно, если известно распределение функции вероятности межатомных расстояний 1У (г".), т. е. значений вектора г^. Тогда среднее значение величины экспоненты в (1.25) будет определяться выражением.

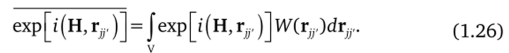
Интегрирование необходимо проводить по всему объему V, где размещаются рассеивающие частицы. Таким образом, функция распределения вероятности межатомных расстояний будет важнейшей и единственной характеристикой структуры с неупорядоченным распределением рассеивающих центров, которую можной получить экспериментально, исследуя рассеянное излучение.