Сходимости в теории вероятностей

Сходимость по вероятности.

Понятие сходимости в теории вероятностей отличается от определения сходимости, принятого в математическом анализе. Напомним, что в математическом анализе последовательность {х"} сходится, если существует такое действительное число а, что для любого положительного е существует номер числовой последовательности п0, начиная с которого для всех членов последовательности справедливо неравенство |х" - а а-еп.

Последнее неравенство означает, что все члены последовательности попадают в е-окрестность числа а за исключением, возможно, конечного числа начальных точек. Рассмотрим последовательность (-1)" 1.

х" =1 н—Если взять е = —, то начиная с номера п₀ — 3 справедливо

п 2

неравенство |х" -1|<�—. На рис. 9.1 построена эта последовательность.

Точками указаны члены последовательности, е-окрестность числа 1,

равная (1-е;1 + е) = —; — , выделена двумя пунктирными линиями, ука- 2 2)

зано число х₃, начиная с которого все члены последовательности ока-

зываются внутри е-окрестности. Число 1 есть предел числовой последо- ( (-1)" ^.

вательности: lim 1± =1.

п-х"^ п)

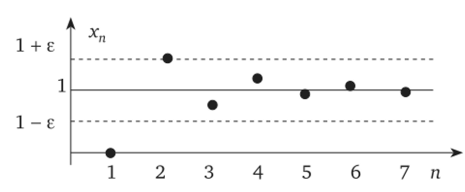
Рис. 9.1. Иллюстрация понятия сходимости.

В теории вероятностей говорят, что последовательность случайных величин {?"} сходится по вероятности (convergence in probability) к случайной величине если для любого положительного числа е вероятность события | ?" -? | < е стремится к единице при п —" со:

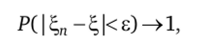
или, что эквивалентно,.

Для сходимости по вероятности {!;"} к принята форма записи: р В этих определениях сходимости и сходимости по вероятности имеется существенное различие. Оно заключается в том, что в случае сходимости по вероятности часть членов последовательности может пребывать вне полосы Е,-г<�х_п<^ + е при каком угодно большом значении п, но вероятность такого события с ростом п становится все меньше.

Приведем иллюстрирующий утверждение пример. Рассмотрим последовательность случайных величин Ъ,_ь ?₂, • ••, %", • ••, каждая из которых имеет свой закон распределения, представленный в таблице.

Каждая случайная величина принимает два значения. На рис. 9.2 значения каждой случайной величины обозначены точками.

Возьмем г=—. В е-окрестность нуля попадает столько же точек, сколько находится вне полосы (-е; е), но вероятность элементарных исходов разная. Подпоследовательность из нулей сходится к нулю с вероятностью Р=——>1 при п —> оо. Подпоследовательность = п п

находится вне е-окрестности. Она расходится (сходится к бесконечности). Вероятность каждого такого исхода равна Р (^" =п) = — —>0. Это.

п

и означает, что последовательность {<;,} сходится к случайной величине? по вероятности. Случайная величина? в данном примере принимает только одно значение, равное нулю.

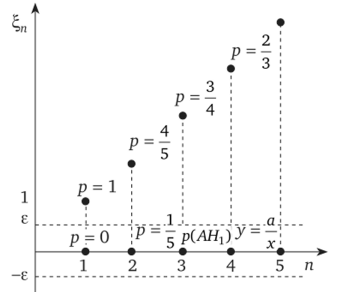
Рис. 9.2. Сходимость по вероятности.

Замечание 9.2. Сходимость по вероятности обладает теми же свойствами, что и обычная сходимость.

Достаточное условие сходимости по вероятности.

Теорема 9.4. Если М (?" - ?,)²—> О при п—>сс, то последовательность случайных величин {?"} сходится по вероятности к случайной величине

t.

?Из неравенства Чебышева следует, что для любого е > О Следовательно, Р (|1~_п — Ъ, > е) —> 0 и в соответствии с определением.

р

сходимости по вероятности —"?,.

Сходимость по распределению.

Рассмотрим последовательность случайных величин {^"}. Каждой случайной величине соответствует некоторая функция распределения. Обозначим через {К (х)} соответствующую последовательность функций распределения. Пусть эта последовательность {F^n (x)} сходится по вероятности к некоторой функции распределения F^Qc) при п —" со в каждой точке непрерывности функции Ft (х). Тогда говорят, что последовательность случайных величин {^"} имеет предельное распределение F?(x), или сходится по распределению (convergence in distribution) к случайной величине.

d

с распределением F=(x), что записывается как Для иллюстрации сходимости по распределению рассмотрим последовательность равномерно распределенных случайных величин.

{%"} — [/ -1—, 1−1—. Этой последовательности соответствует поеледо- п п

вательность функций распределения {F-_n (х)}, таких что.

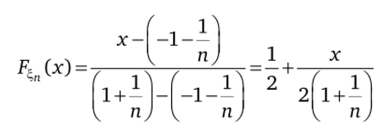
на отрезке -1—; 1н—, а на всей числовой оси п nj.

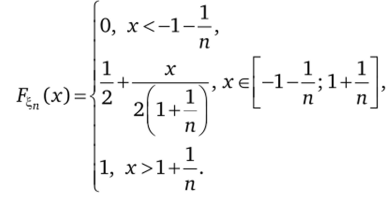
При п —> °о последовательность {F_tn (х)} сходится к функции распределения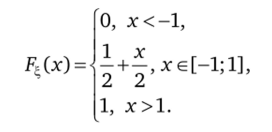

которой соответствует случайная величина ~ [Д-1, +1]. Следовательно, последовательность случайных величин сходится по распределению к случайной величине %.

Таким образом, сходимость по распределению означает, что последовательность случайных величин {%"} сходится к случайной величине если последовательность функций распределения {F_ln (х)} сходится к функции распределения ТДх) в каждой точке непрерывности функции ТДх) при п —> °о.