Вопросы и задания для повторения

• 1. В чем состоит идея метода моментов при построении точечных оценок?
• 2. Какая функция называется функцией правдоподобия?
• 3. Сформулировать теорему метода максимального правдоподобия.
• 4. Что такое стохастическая связь между случайными величинами?
• 5. Когда можно использовать байесовское оценивание?
• 6. Какие статистики называются достаточными?
• 7. Сформулировать теорему факторизации.

Примеры решения задач

х2 X

_р 20 v >П.

Задача 12.1. Функция p*=(x) = 0, задает плот-

0, х<0,

ность распределения Рэлея случайной величины Ъ,. Оценить параметр 0 по выборке X], х₂, …, х_п.

Решение. Посмотрим, как меняется оценка при использовании различных моментов.

1. Воспользуемся математическим ожиданием М?. Приравняем первый начальный теоретический момент (математическое ожидание) первому выборочному начальному моменту (среднему значению):

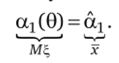
Найдем выборочную характеристику х по выборке, а теоретическую характеристику МЪ, интегрированием:

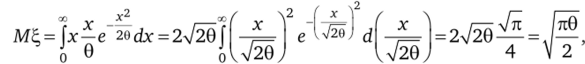
так как, интегрируя по частям, можно получить.

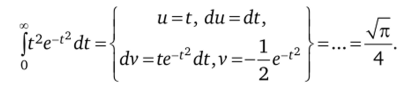
Следовательно, J^ ^{= x}-

л 2х^

Из последнего уравнения находим оценку параметра 0: 0=-.

п

2. Используем второй начальный момент Mi²-. а₂(0) = а₂. Найдем Mi²:

1 ^п

Получим уравнение 20 = — из которого следует П (=1.

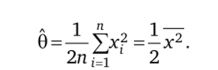
3. Построим оценку на основе дисперсии D^: р₂ = S².

Теоретическая величина дисперсии есть второй центральный момент:

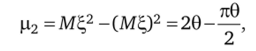
что позволяет составить уравнение.

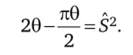
Его решение.

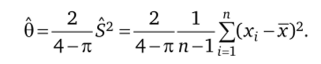
Таким образом, очевидно, что ММ-оценки 0 параметра 0 различны: 23с² 1 — 2 *.

-, —х²,-S². Все они в соответствии с теоремой Слуцкого состоя;

л 2 4-л тельны, так как получены на основе начальных и центральных моментов. Что касается несмещенности, эффективности, асимптотической нормальности, требуются исследования.

Задача 12.2. По выборке х_ь х₂,…, х_п найти оценки параметров, а и, а нормального распределения методом максимального правдоподобия. Решение. Опираясь на плотность нормального распределения ^ О-а)²

р*(х)=—j=e 2а² _г при наличии результатов п испытанийх_1; х₂, …, х" сту2л выпишем логарифмическую функцию правдоподобия:

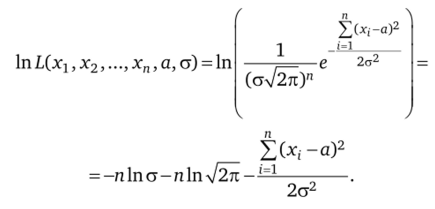
Найдем координаты критической точки, решив систему уравнений, получающихся приравниванием первых двух частных производных по неизвестным параметрам к нулю:

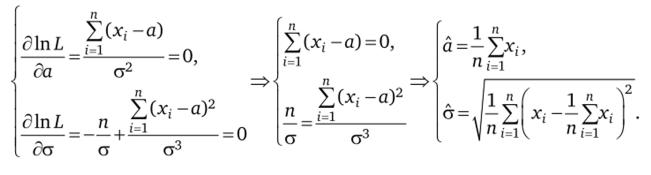
Для исследования критической точки на максимум составим матрицу из вторых производных и найдем значения элементов матрицы в критической точке:

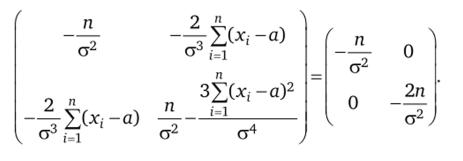
Убедимся в том, что угловые миноры М_ь М₂ чередуются по знаку,, п _, 4п .

начиная с отрицательного: М₁ = —— < О;М₂ =—> 0, что говорит о нали;

а² ст⁴

чии максимума. Оценки параметров, а и о есть координаты критической точки аист.

Задача 12.3. Методом максимального правдоподобия по выборке х_х, х₂, …, х_п найти оценки параметров а и b равномерного распределения.

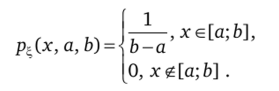
Решение. Условие теоремы 12.1 (п. 1) не выполнено. Исследование производной, возможно, не приведет к успеху, так как не выполнено одно из условий теоремы. Тем не менее составим функцию правдоподобия:

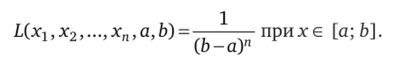
Элементы вариационного ряда разместим по возрастанию: x_min, x_max ^и учтем, что x_min > a, x_max < b. Анализ функции правдоподобия показывает, что с убыванием Ъ разность Ъ — а убывает и, следовательно, функция L растет, достигая наибольшего значения в точке b_min = = x_max. Аналогично при фиксированном b с ростом а функция L растет и достигает наибольшего значения в точке a_max = x_min. Таким образом, оценками параметров а и b будут крайние члены вариационного ряда.

^а ~ *min> ^ ^— *тах;

Задача 12.4. Случайная величина ?, распределена нормально с математическим ожиданием 0 и дисперсией а². Собранная о величине 0 информация позволяет предположить, что она ведет себя как нормально распределенная случайная величина с нулевым математическим ожиданием и известной дисперсией о^:

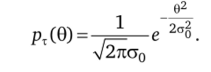
Имеются результаты п наблюдений случайной величины q. Построить байесовскую оценку параметра 0.

Решение. Поскольку априорное распределение параметра 0 имеется, перейдем к нахождению функции максимального правдоподобия:

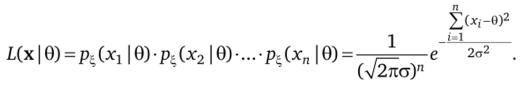
Вычислим числитель апостериорной плотности вероятностей, зависящий от 0:

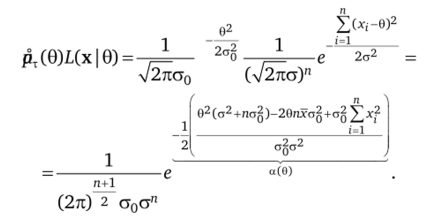
В приведенном выражении рассмотрим отдельно обозначенный через а (0) показатель, разделив его числитель и знаменатель на а² + па%

и введя обозначения а =™^CG° = —_и D² = ^СТ°^СТ = —^g°: а² + nag _{1 +} _aj_ a²+nag _{1 +} «^о.

na^ а²

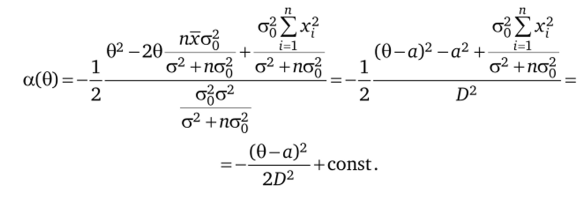
Знаменатель апостериорной плотности вероятностей не зависит от 0, представляя собой вместе с другими константами нормирующий множитель. Поэтому апостериорное распределение с плотностью С 0-а)²

р_т (01 х) ~ е 2D² _> аккумулирующее в себе как априорную, так и выборочную информацию о параметре 0, снова является нормальным со средним значением а и дисперсией D². Соответственно, байесовская.

^Л X

оценка параметра 0 определяется формулой 0_Б =-— с дисперсией.

i+4.

по²

А Л.

D² =-. С ростом п оценка 0_Б приближается к оценке 0_ММП = х пара;

_{1 +} п*1

а²

метра 0, найденной по методу максимального правдоподобия.