Специфика процедур оптимизации (с учетом грузовместимости ТС)

Напомним, что для оптимального интервала повторного заказа Т0 и оптимального размера заказа q0 при оптимизации с учетом фактора грузовместимости ТС ранее в этой главе были доказаны новые универсальные формулы [см. также: 31, 33, 34]. Речь идет о следующих формулах. Параметр Т0 определяется как Т0 = q0 / D, причем для q0 имеет место равенство (3.4). Для удобства изложения приведем здесь указанное равенство в качестве равенства (3.10):

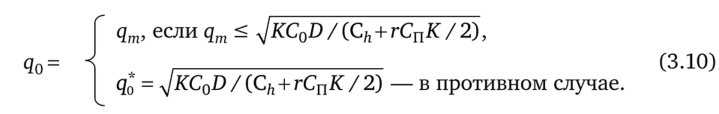
Кстати, использованный в (3.10) показатель cfo = q_onT = = jKC₀D / (C_h + rC_nK / 2) для размера заказа соотносится именно с оптимальным размером заказа, но только при оптимизации соответствующей модификации EOQ-модели без ограничений на грузовместимость ТС (см. гл. 1—2). При этом для процентной ставки г имеет место оценка.

(3.3), которая была получена ранее в гл. 1—2 (применительно к конкретному значению параметра К).

Кроме того, если при оптимизации поставок не требуется учитывать ВЦД, то равенство (3.10) примет вид (3.10*):

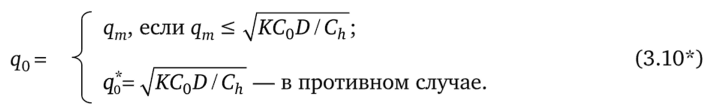
В отличие от моделей гл. 1—2 (когда рассматривался более простой случай оптимизации без учета грузовместимости ТС, но с учетом конкретного значения для параметра К), чтобы использовать формулы.

(3.10) при оптимизации модели надо учесть следующее, а именно надо только потребовать, чтобы все затраты, связанные с поставками (помимо вложенного оборотного капитала) можно было реализовать из выручки, полученной на текущем интервале повторного заказа. При этом условие, состоящее в том, что грузовместимость ТС (см. показатель q_m) не должна мешать разместить в ТС заказ (найденного оптимального размера q₀) будет выполнено автоматически с учетом (3.10).

Для анализируемой ситуации требуемые ограничения, которые надо наложить на EOQ-модель, будут следующими.

• 1. Выручка к моменту Т₀ / 2 (после вложения в начальный момент времени оборотного капитала для работы цепи поставок) должна быть достаточной, чтобы покрыть издержки хранения и требуемые бизнесом отчисления на интервале [0; Т₀]. Такие выплаты для модели с учетом грузовместимости составляют q₀ [L_n + C_hT₀ / 2].
• 2. К моменту Т₀ выручка, получаемая на интервале [0; Т₀], должна быть достаточной для оплаты дополнительно и очередной поставки, чтобы осталась прибыль. Речь идет о затратах величины С₀ + q₀C_n, так как именно такая сумма требуется в момент Т₀для оплаты очередного заказа и его поставки.

Как и в более простом случае, рассмотренном в гл. 1, учитывая фактор постоянного спроса в формате EOQ-модели, для выручки V (0 (на интервале времени [0; Т₀]) имеет место равенство: V (t) = = tD (С_п + Р_п). Поэтому первое из указанных выше условий записывается как V (Г₀ /2) > q₀ [L_n + C_hT₀ / К]. Такое условие представим более просто в виде неравенства.

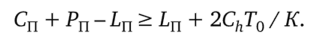
Для второго условия имеем V (Т₀) > С₀+ q₀ (С_п + L_n +C_hT₀ / К). Здесь учтено, что после указанных выше выплат в момент времени Т₀ / 2 выручка к моменту времени Т₀ должна быть достаточной для того, чтобы дополнительно оплатить очередную поставку (т. е. сумму С₀ + то формализуется в виде неравенства:

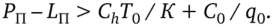
В формате рассматриваемой модели с учетом грузовместимости ТС к найденным двум условиям не требуется добавлять еще одно, как это надо делать для более простых моделей гл. 1—2. Действительно, здесь учет фактора грузовместимости реализуется при определении параметров оптимальной стратегии.

Итак, необходимым и достаточным условием, при котором можно реализовать требуемые выплаты из выручки в формате процедур оптимизации, которые учитывают грузовместимость ТС, является выполнение системы из двух неравенств:

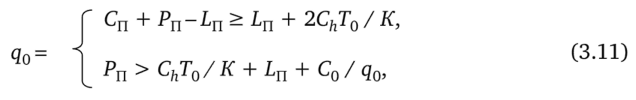
где Т₀ = q₀ / D, a q₀ определяется равенством (3.10).

Обратим внимание на то, что второе неравенство в системе (3.11) имеет очевидную экономическую интерпретацию, а именно прибыль с каждой единицы поставляемого товара должна покрывать следующие удельные (связанные с единицей товара) расходы:

• • на ее хранение (с учетом специфики таких выплат);
• • поддержку бизнеса (в виде требуемых отчислений размером L_n);
• • поставку (в смысле удельных таких затрат на единицу товара).

При этом дополнительно отметим, что указанное второе неравенство в системе (3.11) можно также переписать в виде DP_n > DL_n + + C_hq₀ / К + С₀ /Т₀ (для этого следует умножить обе части указанного неравенства на D). Таким образом, можно дополнительно отметить, что это неравенство имеет свою очевидную интерпретацию: суммарная годовая прибыль должна покрывать все расходы на поставку и хранение товара, а также требуемые отчисления на поддержку бизнеса.

Результат проведенного анализа, представленный системой неравенств (3.11), в общем случае зависит от того, потребует ЛПР или нет при оптимизации поставок учитывать ВЦД. Чтобы избавиться от такой зависимости, можно применить подход, уже использованный ранее, — вместо указанных условий (3.11), где надо задействовать соответствующую для моделируемой цепи поставок процентную ставку г, можно перейти к достаточным условиям такого типа, которые не будут использовать указанную процентную ставку. Для этого при определении показателей Т₀и д₀надо применить не соотношения (3.10), а соотношения (3.10*). Такая процедура приведет к большим по величине значениям указанных показателей, чем в ситуации, когда эти показатели определяются с учетом ВЦД, поскольку знаменатель соответствующего подкоренного выражения становится меньшим. При этом выполнение системы неравенств (3.11), как нетрудно видеть, становится достаточным условием, выполнение которого обеспечит требуемые выплаты из выручки на интервале повторного заказа.

Проверка условий (3.11) должна предшествовать процедурам формализации окончательного решения об организации поставок. Это не представляет трудностей при моделировании реальных цепей поставок, что легко проиллюстрировать при моделировании численной ситуации. Требуемые процедуры принятия решений покажем на следующем примере.

Пример 3.2.

Рассмотрим цепь поставок для EOQ-модели управления запасами, представленной ранее в примере 1.1 (гл. 1). Надо учесть, что издержки хранения оплачиваются по занятым местам на складе (т. е. надо учесть, что К = 2). Принято также, что издержки хранения и отчисления на дополнительные затраты бизнеса должны оплачиваться из выручки, причем в середине интервала повторного заказа. Дополнительно к модели примера 1.1 будет учтена грузовместимость ТС. Представим параметры модели:

D = 1200 — годовое потребление, ед. тов.;

С₀= 96 000 — расходы на одну поставку, руб.; представляют издержки, которые не зависят от количества поставляемых единиц продукции;

С_п= 12 000 — стоимость покупки / себестоимость единицы товара, руб.;

Р_п= 3000 — прибыль от реализации единицы товара, руб.;

L_n = 1000 — отчисление из выручки на единицу товара, руб.; такое обобщение позволяет учитывать специальные затраты, пропорциональные объему поставок: бонусные выплаты, издержки страхования, возможность хеджирования рисков ит.д.;

q_m = 150 — максимально допустимый размер заказа, который можно разместить в ТС с учетом его грузовместимости, ед. тов.;

C_h = 2560 — издержки хранения единицы продукции за год, руб.; при этом моменты времени выплат таких издержек для каждой партии заказа соотносятся с серединами периодов повторных заказов;

Требуется

В формате заданной EOQ-модели реализовать следующие процедуры анализа.

• 1. Надо установить, можно ли для цепи поставок применительно к такой EOQ-модели использовать отмеченные ранее в этой главе процедуры оптимизации решений о поставках с учетом ВЦД.
• 2. Проиллюстрировать полученный результат, моделируя денежные потоки такой цепи поставок.

Решение

1. Сначала по формуле (3.10) надо определить параметры q₀ и Т₀ для такой модели управления запасами (учитывая, что К = 2). Для этого на основе оценки (3.3), которая была приведена в этой главе применительно к процентной ставке г (применительно к случаю К = 2), предварительно отмечаем следующее.

В формате такой цепи поставок для рентабельности оборотного капитала можно использовать показатель г = 0,4415 (или 44,15%). Кроме того, учитывая снова, что К =2, определяем показатель д для поставок без учета фактора грузовместимости. Получаем, что q_0Irr = ^KC₀D / (C_h+ гС_пК / 2) = 171 (после округления до целых единиц товара). Соответственно, по формуле (3.10) для оптимального размера заказа с учетом фактора грузовместимости находим, что q₀ = 150, а для оптимального интервала повторного заказа Г₀ получаем значение Г₀ = 1/8.

Как видим, требуемый оборотный капитал для такой цепи поставок составляет 96 000 +150 • 12 000 = 1 896 000 руб. Теперь проверим, выполняется ли система неравенств (3.11). Указанные условия для такой ситуации будут представлены следующими двумя неравенствами, в которых уже учтено, что q₀ = 150 ед. тов. и Т₀ = 1 / 8 = 0,125 года:

Эти неравенства выполняются. Таким образом, для соответствующей цепи поставок будет выполнено следующее. С одной стороны, выручка на интервале повторного заказа будет покрывать требуемые затраты, связанные с такой поставкой (с учетом указанного выше оборотного капитала). Кроме того, найденный оптимальный размер заказа q₀ — 150 можно будет разместить в ТС с учетом его грузовместимости (это автоматически было обеспечено решением в (3.10)). Как видим, для указанной модели можно применять предложенные в этой главе процедуры оптимизации.

2. Теперь проиллюстрируем полученный результат применительно к денежным потокам такой цепи поставок. Напомним, что в контексте проведенного анализа это подразумевает выполнение следующих двух условий. Первое из них требует, чтобы выручка к моменту Т₀ / 2 была достаточной, чтобы покрыть издержки хранения и отчисления на поддержку бизнеса, которые соответствуют интервалу времени [0; Т₀]. Для моделируемой цепи поставок (при К = 2) такие выплаты, как легко видеть, составляют [q₀C_hT₀ /2 + д^_п ] = 24 000+ 150 000 = 174 000 руб. Поскольку выручка к указанному моменту времени Т₀ / 2 принесет сумму q₀ [С_п + + Р_п] / 2 = 150 • (12 000 + 3000) /2=1 125 000 руб., то возможность указанной выплаты из выручки очевидна.

Второе из указанных условий требует, чтобы выручка к моменту Г₀ была достаточной для оплаты еще и требуемых затрат на очередную поставку. Такие затраты для моделируемой цепи поставок составят С₀ + q₀C_n = 96 000 + 150? 12 000 = 1 896 000 руб. В то же время выручка к моменту Т₀ принесет (за вычетом указанных выше оплаченных издержек в виде суммы 174 000 руб.) 2 250 000 — 174 000 = 2 076 000 руб. Как видим, ее снова вполне хватит, чтобы покрыть указанные очередные затраты на очередную поставку, которые, как уже было показано, составляют 1 896 000 руб. При этом в формате одного интервала повторного заказа останется прибыль в размере 180 000 руб. Это позволит получить годовую прибыль объемом 8 • 180 000 = 1 440 000 руб. Проверьте самостоятельно, что после представленных процедур оптимизации для стратегии поставок при требуемом оборотном капитале размером в 1 896 000 руб. его рентабельность существенно увеличится и составит 75,95% (как и следовало ожидать по результатам исследований, представленных в гл. 1—2). Указанный результат для рентабельности оборотного капитала будет получен вместо показателя рентабельности 44,15%, который обеспечивает оптимизация без учета ВЦД.

Таким образом, в данной главе проведен анализ целесообразности одновременного использования нескольких ТС для поставок товара в задачах управления запасами, если предоставляются скидки на издержки поставок при увеличении числа совместно используемых для этого ТС. Рассмотрены новые постановки таких задач оптимизации применительно к моделям теории управления запасами на основе EOQ-формулы. Они позволят менеджеру принимать во внимание грузоподъемность/грузовместимость ТС с дополнительным учетом как специфики условий оплаты издержек хранения, так и требования, соотносимого с необходимостью учета временной ценности денег. Найдено и доказано соответствующее необходимое и достаточной условие, которое устанавливает приемлемый уровень указанного дисконта, чтобы одновременные поставки сразу несколькими ТС (при произвольном числе п таких ТС) смогли оказать конкуренцию традиционным альтернативным решениям по организации поставок при управлении запасами. Приведенные в работе числовые примеры проиллюстрировали эффективность предложенного подхода к определению наилучших решений при оптимизации цепей поставок для классических задач теории управления запасами.

Представленные в исследовании, выполненном в этой главе, материалы также проиллюстрировали, что полученные здесь результаты надо учитывать при оптимизации реальных систем управления запасами. Модификация соответствующего алгоритма оптимизации будет приведена в следующей главе.