Множественная (многофакторная) регрессия

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии:

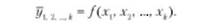
Построение моделей множественной регрессии включает в себя несколько этапов:

• 1) выбор формы связи (уравнения регрессии);
• 2) отбор факторных признаков;
• 3) обеспечение достаточного объема совокупности. Определение типа уравнения затрудняется тем, что для любой формы зависимости можно выбрать целый ряд уравнений, которые в определенной степени будут описывать эти связи. Особое значение имеют линейные модели в силу простоты и логичности их экономической интерпретации.

Важным этапом построения уравнения множественной регрессии является отбор и последующее включение в него факторных признаков.

С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема и требует больших временных затрат. Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.

Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена па основе интуитивно-логических или многомерных математико-статистических методов анализа.

Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в реализации алгоритмов последовательного включения, исключения или включения-исключения факторов в уравнение регрессии с последующей проверкой их статистической значимости.

При использовании алгоритма включения факторы поочередно вводятся в уравнение регрессии так называемым прямым методом. При проверке значимости введенного фактора определяется, насколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции (К2).

Сущность алгоритма последовательного исключения заключается в том, что отбрасываются факторы, ставшие незначимыми по^{-критерию} Стьюдента или другим статистическим критериям. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значения коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения.

Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а значение коэффициента регрессии не изменяется (или меняется несущественно), то данный признак существенен и его включение в уравнение регрессии целесообразно. В противном случае фактор нецелесообразно включать в модель регрессии.

При построении модели регрессии возможна проблема мультиколлинеарности, под которой понимается тесная корреляционная зависимость между факторными признаками, включенными в модель (гх > 0,8).

Наличие мультиколлинеарности между признаками вызывает искажение величины параметров модели, которые имеют тенденцию к завышению, чем осложняется процесс определения наиболее существенных факторных признаков и искажается смысл экономической интерпретации коэффициентов регрессии.

Можно выделить следующие причины возникновения мультиколлинеарности между признаками:

• • изучаемые факторные признаки являются характеристикой одной и той же стороны изучаемого явления или процесса. Например, показатели объема производимой продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер предприятия;
• • факторные признаки являются составляющими элементами друг друга. Например, показатели выработки продукции на одного работающего и численность работающих одновременно в модель включать нельзя, так как в основе расчета показателей лежит один и тот же показатель — численность работающих на предприятии;

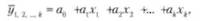
• факторные признаки, но экономическому смыслу дублируют друг друга.

Устранение мультиколлинеарности может реализовываться через исключение из корреляционной модели одного или нескольких линейно-связанных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы.

Вопрос о том, какой из факторов следует отбросить, решается на основе качественного, логического анализа изучаемого явления, а также анализа тесноты связи между результативным и каждым из сильно коллинеарно связанных факторных признаков. Из дальнейшего анализа целесообразно исключить тот факторный признак, связь которого с результативным наименьшая.

Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Исследователь должен стремиться к увеличению числа наблюдений, так как большой объем наблюдений является одной из предпосылок построения адекватных статистических моделей.

Аналитическая форма зависимости результативного признака от нескольких факторных выражается многофакторным (множественным) уравнением регрессии или моделью связи.

Линейное уравнение множественной регрессии имеет следующий вид:

где г/, 2 к — теоретические значения результативного признака, полученные в ходе подстановки соответствующих значений факторных признаков в уравнение регрессии; а, а2, ак — параметры модели (коэффициенты регрессии); х1, х2, хк — факторные признаки.

Параметры уравнения могут быть определены методом наименьших квадратов.

Пример. Определим взаимосвязь между основными показателями деятельности малых предприятий Центрального федерального округа РФ (табл. 7.6).

Система нормальных линейных уравнений имеет следующий вид:

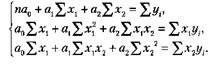
Таблица 7.6. Основные показатели деятельности малых предприятий Центрального федерального округа РФ в 2010 г.

Определим параметры линейного уравнения регрессии (табл. 7.7).

Таблица 7.7. Расчетная таблица для определения параметров уравнения регрессии оборота малых предприятий Центрального федерального округа РФ

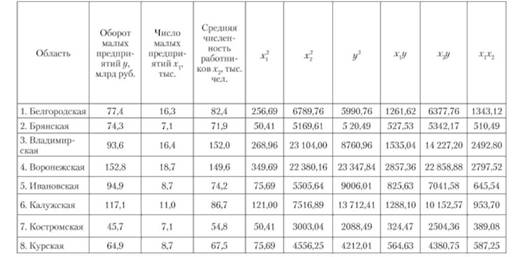
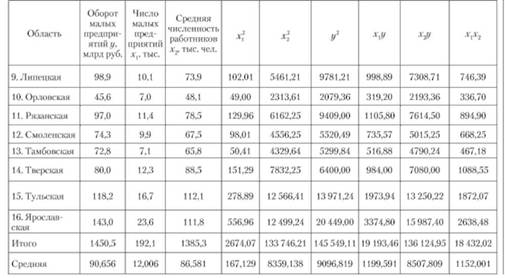
Составим систему уравнений:

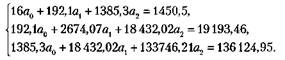
Таким образом, уравнение множественной регрессии имеет следующий вид: