Типичные статистические распределения и их параметры

При решении практических задач по надежности и безопасности функционирования сложных систем наиболее широкое применение нашли такие статистические распределения, как биномиальное, нормальное, показательное, пуассоновское, равномерное, а также распределения Стьюдента, Фишера и хи-квадрат, которые используются для аппроксимации различных случайных величин. Ознакомимся с некоторыми из них.

1. Биномиальное распределение относится к дискретным случайным величинам X и рекомендуется для оценки параметров их распределения при испытаниях в практически неизменных условиях, т. е. по так называемой схеме Бернулли. В частности, оно применяется для прогноза вероятности Р (Х = т) появления т случайных исходов в п опытах, в предположении о равной вероятности р возникновения регистрируемого события в каждом из них:

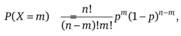(2.24).

где n! и m! — факториалы.

Данное распределение характеризуется двумя числовыми характеристиками: математическим ожиданием т = пр, дисперсией D = nр (1 — р) и используется для интерпретации случайных событий типа отказ или происшествие.

2. Нормальное (Лапласа — Гаусса) распределение названо так из-за большой распространенности и естественной формы графического представления его плотности вероятности (колоколообразная палатка — см. рис. 2.6, б). Это распределение относится только к непрерывным случайным величинам, а его плотность вероятности выражается формулой.

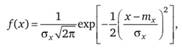(2.25).

где т_к, ?_х — математическое ожидание и стандартное отклонение случайной величины X.

Сфера практического применения данного распределения чрезвычайно разнообразна, в чем можно будет убедиться ниже, например при изучении результатов распространения вредного вещества в атмосфере и прогнозирования остаточного ресурса технических систем (времени до наступления в них так называемого предельного состояния). А одна из его модификаций (когда т_х = 0, ?_v = 1) названа стандартным нормальным распределением, которое представлено в табличной форме практически во всех литературных и нормативных источниках по теории вероятностей и математической статистике.

3. Показательное, или экспоненциальное, распределение также может иметь лишь непрерывная случайная величинах, и только на отрезке от 0 до +?. При этом плотность ее вероятности определяется следующим выражением:

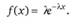(2.26).

Данный тип распределения имеет единственную числовую характеристику ?, обратную величину которой b = 1/? принято называть параметром масштаба. Оно широко применяется для описания моментов времени отказа сложных технических систем на установившейся стадии их эксплуатации, а также при интерпретации потоков событий, входящих и выходящих из так называемых систем массового обслуживания. Дополнительные и более конкретные сведения, касающиеся уникальной особенности, графического представления и сфер применения экспоненциального распределения, будут изложены несколько ниже (например, см. гл. 3 и 18).

4. Распределение Пуассона (закон редких событий) получается из биномиального при п>?, Р>0 и когда пР = const. Оно относится к дискретным случайным величинам, позволяя рассчитывать вероятность появления любого наперед заданного количества т каких-то случайных событий по следующей формуле:

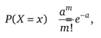(2.27).

где а — единственный параметр этого распределения, являющийся и m, и D.

Наиболее широкое распространение это распределение нашло при количественном описании закономерностей возникновения различных техногенных происшествий на производстве и транспорте, так как их появление в одном и том же месте является сравнительно редким событием, что и подтверждается его названием.

5. Равномерное (прямоугольное) распределение может характеризовать как непрерывную, так и дискретную случайную величину X, а его плотность имеет следующий вид:

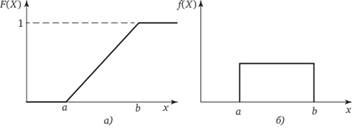
Рис. 2.7. Графики равномерного распределения:

а — функция распределения; б — плотность где а, b — константы, выбираемые с соблюдением следующего условия: а <�х

Данное статистическое распределение является самым неинформативным (обладает максимальной энтропией) и имеет два параметра: 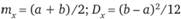. Наибольшее распространение равномерный закон нашел при имитационном (статистическом) моделировании с применением цифровой вычислительной техники, где его используют для настройки различных датчиков и генераторов случайных чисел.

Графики плотности и функции распределения для равномерного распределения показаны на рис. 2.7, а пример их практического использования при имитационном моделировании происшествий при функционировании системы «человек — машина — среда» изложен в гл. 11.

Что касается других упомянутых выше распределений, то они описываются более сложными функциональными зависимостями и применяются в качестве вспомогательных соотношений при обосновании решений в интересах менеджмента надежности и техногенного риска, а также для решения ряда задач математической статистики.