Линейные регистры сдвига и линейные рекуррентные последовательности

Линейное преобразование пространства Р^п над полем Р не является п.ц. при п > 0, так как нулевой вектор является неподвижным элементом всякого линейного преобразования. Все же длина цикла в графе линейного преобразования пространства Р^п может быть при больших п весьма большой и достигать величины kⁿ — 1, где k — порядок поля Р. Такие линейные преобразования называют преобразованиями максимального периода.

Определим условия максимальности периода подстановки g пространства Р*^г линейного регистра левого сдвига (ЛPC) с обратной связью а_п__хх_п + + … + а_хх₂ + %r_t, где а_п__х> …, а_х, а₀ е Р. Матрица A_g преобразования g, называемая сопровождающей матрицей J1PC, имеет вид.

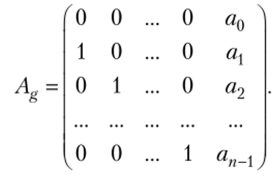
Следовательно, если х = (х_х> …, х_п), то g (x) = xA_g. ЛРС длины п максимального периода обозначим ЛРСтах-я. Особый интерес в криптологии к ЛРСтах-я объясняется удобством их реализации и доказуемостью больших длин периодов (при подходящих п) в отличие от многих нелинейных преобразований. Ведь «лобовое» вычисление длины периода (см. пример 8.1) выполнимо лишь для преобразований множеств небольшой мощности.

Преобразование g ЛРС имеет максимальный период <=" циклическая группа (g) имеет порядок kⁿ — 1, иначе, orcL4_g= kⁿ — 1 в группе линейных подстановок множества Р'⁷. Выразим эти условия через характеристики обратной связи. Функции обратной связи f (x_i9 х") ЛРС однозначно соответствует многочлен F (X) степени п над полем Р:

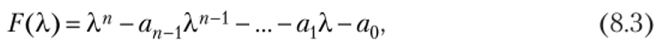
называемый характеристическим многочленом этого ЛРС. Матрица A_g является корнем многочлена F (X), и если F (X) неприводим над Р, ее порядок совпадает с порядком многочлена F (X). Значит, длина периода g максимальная F (X) — примитивный многочлен, т. е.:

• 1) F (X) неприводимый над нолем Р;
• 2) ordF (X) = kⁿ — 1, т. е. F (X) делит многочлен X^k" ~^x -1 и не делит ни один из многочленов вида X^d — 1, где d делит kⁿ — 1 и d Ф kⁿ — 1.

Построение примитивных многочленов большой степени связано со сложными вычислениями. На практике используются таблицы примитивных многочленов.

Для ряда двоичных ЛРС условие максимальности периода упрощается.

Утверждение 8.4. Если многочлен F (X) степени п > 1 неприводим над нолем GF (2), и число 2″ - 1 простое (число Мсрсенна), то подстановка g с характеристическим многочленом F (X) имеет максимальный период.

А Лишь один делитель d простого числа 2″ - 1 отличен от самого числа, а именно, d = 1, тогда при п > 1 многочлен F (X) не делит X © 1. По следствию из теоремы 4.16 и по теореме 4.17 порядки корней многочлена F (X) равны ordF (X) и равны 2^п — 1. Следовательно, F (X) примитивный. ?

Утверждение 8.5. Примитивный многочлен F (X) над GF (2) имеет нечетный вес.

Ч Иначе единица поля GF (2) есть корень F (X) и по теореме Безу А, © 1 делит F (X). ?

Утверждение 8.6. Если многочлен F (X) над GF (2) примитивный, то и многочлен XⁿF ( 1 / X) примитивный. [>

Эго свойство в два раза сокращает таблицы примитивных многочленов над GF (2).

Порождение псевдослучайных последовательностей, используемых в криптографических приложениях, основано на реализации многократных итераций преобразований конечного множества. Одним из базовых элементов криптографических систем является регистр сдвига. Рассмотрим свойства координатных последовательностей, порождаемых регистрами.

Последовательность X= {x_jy i = О, 1, …} над конечным множеством X называется рекуррентной последовательностью (PIT) порядка п > 0 над X, если найдется функция f:Xⁿ—>X такая, что для любого i > О.

Равенство (8.3) называют законом рекурсии, функцию / — генератором РПа вектор (х₀, x"__t) — начальным вектором РП. При х = k обозначим РП порядка п через РП (&, п). Из закона рекурсии следует, что длина периода РП (/г, п) не превышает kⁿ.

Между множеством всех РП (?, п) и множеством регистров сдвига длины п над X имеется биекция ср. Если генератором РП (&, п) является функция /обратной связи регистра, то данная РП с начальным вектором (x_0f…, х_п__х) есть 1-я координатная подпоследовательность Х_хпоследовательности jg^(x₀, …, х_п__х), где jg — преобразование X" , реализуемое регистром. При этом j-я координатная подпоследовательность Xj_+ последовательности х_п__х) отличается от Х_х_+ лишь сдвигом на j — 1 знак,.

j = 2,…, п. Поэтому в соответствии с теоремой 8.2 длины периода и предпериода РП (/е, п) с начальным вектором (х₀,…, х_п__х) совпадают соответственно с длинами периода и предпериода последовательности fg^(x₀, …, х_п__х) (см. утверждение 8.2). В частности, РП (&, п) с начальным вектором (х₀>…, х_п__х) чисто периодическая (х₀, …, х_п__х) циклическая вершина в графе преобразования fg.

Наилучшие криптографические свойства имеют последовательности с экстремальными периодическими свойствами. Важным является также удобство (простота) технической или программной реализации генератора РП. Рассмотрим РП с линейным законом рекурсии.

РГ1(/г, п) над нолем Р называют линейной рекуррентной последовательностью (обозначается ЛРП (&, п))_у если при ненулевом наборе (а₀, …, а_п__х) е Р^п и любом i > 0 верно:

Иначе говоря, генератором ЛРП является линейная функция /: Р^п —> Р. Связанный с линейным законом рекурсии многочлен Р (А) над полем Р, заданный равенством (8.3), называют характеристическим многочленом ЛРП. ЛРП порядка п при Р = k обозначим через ЛРП (&, п).

Не теряя общности, положим я₀ * 0- Иначе а₀ = … = а,.__х = 0 и а_г Ф 0, где О <�г<�п, тогда совпадают законы рекурсии и периоды характеристических многочленов Р (А) и Р (А) / А/, где многочлену Р (А) / А^; соответствует Л РП (&, п — г).

Ограничение биекции ф на множество Л PC длины п над Р есть биекция с множеством всех ЛРП (&, я), сохраняющая их характеристические многочлены. Тогда ЛРП (&, п) есть 1-я координатная подпоследовательность последовательности fg^(x₀,…, х_п__х), и при а₀ Ф О ЛРП (&, п) является чисто периодической. Длина ее периода совпадает с длиной цикла подстановки jg, содержащего вектор (д:₀,…, х_п__х). Следовательно, ЛРИ (/е, п) с максимальной длиной периода (обозначим ее ЛРПтах-w) порождается при ненулевом начальном векторе характеристический многочлен ЛРП(k, п) примитивен.

Для ЛРП (&, п) с характеристическим многочленом F (X) обозначим: If (х₀,x_n_f) Р^[1] —" Р — функция, отображающая множество начальных векторов во множество значений i-го члена генерируемой ЛРП, i = 0,1,… (назовем ее i-й выходной функцией ЛРП). Следовательно, If (х₀,…, х_п__х) = и ((0)‘(х_о, х^)), где v (y₀, у_п__{) = у₀ для любого (г/₀, …, у_п__х) е Р". Обозначим:

= {//*(Xq,…,^-!), i = 0, 1,…} — последовательность всех выходных функций ЛРП, t_F — длина периода последовательности U_+.

Утверждение 8.7. Для ЛРП (&, п) с характеристическим многочленом F (X) последовательность LF+ состоит из линейных функций от х₀, …, х_п__х, и t_F = ord (^) n — 1. Для ЛРПтах-т? L^F_^ состоит из всех линейных функций, отличных от константы 0, и t_F= kⁿ — 1.

^ Любая выходная функция ЛРП отлична от константы 0 и линейна, так как линейна функция обратной связи jg ЛРС.

Последовательность И_^ представима как последовательность таблиц выходных функций, которая есть сопряжение множества ЛРП (&, п) с характеристическим многочленом Р (А.), порождаемых при всех начальных векторах (х_0у …, х_п__х) е Р^п. Длина периода ЛРП (&, п) при начальном векторе х = (х₀, …, х_п__х) равна длине цикла подстановки fg, содержащего вектор .г, тогда в соответствии с теоремой 8.2а t_F= НОК (/,…, l_k) = ord (yg), где /j,…, 4 ^— длины циклов линейной подстановки fg. Известно^[1], что граф любой линейной подстановки содержит цикл длины /, кратной длине каждого цикла этой подстановки. Следовательно, t_F= /, где /< kⁿ — 1.

Граф линейной подстановки максимальной длины периода состоит из двух циклов, длина которых равна 1 и kⁿ — 1, т. е. в этом случае t_F=kⁿ — 1.

Покажем, что в случае ЛРПтах-и на периоде D^ нет одинаковых функций. Если это не так, т. е. If (х₀,…, х_п__х) = If (х₀,…, х_п__х), где 1 < i < kⁿ — 1, то в ЛРП при любом начальном векторе (х₀, …, х_п__х) имеются совпадения на расстоянии j — i, что в соответствии с утверждением 8.1а противоречит максимальности длины периода ЛРП. ?

Отметим важные статистические свойства ЛРПтах-/?.

Утверждение 8.8. На периоде ЛРПтах-/? над полем Р порядка k всякая ненулевая (нулевая) 5-грамма встречается kⁿ~^s раз (kⁿ~^s — 1 раз), 1.

Ч Период ЛРПтах-я есть последовательность {(x_i} … yX_n__Ui)_} i = 0, …, kⁿ — 2}, состоящая из всех ненулевых я-грамм (векторов пространства Р"). Поэтому частота встречаемости на периоде ЛРПтах-я любой 5-граммы есть число ненулевых векторов пространства Р'⁷, у которых 5 первых координат совпадают с заданной 5-граммой. ?

Итак, частоты 5-грамм распределены в ЛРПтах-и почти равномерно. Вместе с тем в силу закона рекурсии (8.5) в ЛРП (&, п) имеется межзнаковая зависимость, позволяющая по любой я-грамме ЛРП(k, п) определить все остальные знаки. При использовании в криптосистемах ЛРС предусматривается усложнение соответствующей ЛРП.

• [1] Гантмахер Ф. Р. Теория матриц. М.: Наука, 1988.
• [2] Гантмахер Ф. Р. Теория матриц. М.: Наука, 1988.