Метод Матано в паре образцов бесконечной толщины

Для определения ДО пользуются следующим методом. Берут два бруска твёрдого раствора с различным содержанием растворённого вещества (диффузанта) и приводят в тесный контакт. Такой сложенный образец нагревают до определённой температуры и выдерживают известный промежуток времени. В процессе отжига атомы способные к миграции переходят с части образца с большим содержанием диффузанта Сх в часть с меньшим его содержанием С2. В результате создаётся распределение концентрациидиффузанта, которое и измеряется методом продольного среза или методом снятия слоёв. Расчёты проводят методом Матано.

Если обе части образца достаточной длины и продолжительность отжига не очень велика, то изменение концентрации не успевает произойти во всём теле образца и можно считать, что он простирается бесконечно далеко вправо и влево от плоскости раздела х=о.

Если в начальный момент времени концентрация в одной пластине С" а во второй С₂, то справедливо условие: ^Cj_xdc=0 •.

CI.

Это условие определяет плоскость, которую называют поверхностью Матано^сд/. Так как величина D зависит от концентрации, то количество диффузанта, проходящего через плоскость х=х₀ в единицу времени справа налево, не равно потоку слева направо и плоскость х=хм смещается в течение изотермического отжига образца. Для определения D© необходимо знать всю кривую C (x, t) в области от С₂ до С или от С_х до С и затем провести численное дифференцирование и интегрирование, связанные с трудно контролируемыми ошибками и весьма трудоёмкие. Вычислительные трудности усугубляются необходимостью определения х.м. Матановская граничная плоскость — плоскость, по обе стороны которой равны интегралы концентрации, измеренные в каждый момент диффузии.

Вследствие неравномерного протекания диффузии в областях с различной концентрацией концентрационный профиль тоже становится асимметричным, из-за чего плоскость Матано смещается. Физически плоскость Матано представляет собой сечение образца, через которое в данный момент времени в обе стороны диффундирует одно и то же число атомов. В.

А= - Const,.

широком интервале значений С, при C=const, то XM=const. Если.

D=const, то a’j =Const, если D=J[C), то Хм изменяется во времени.

В методе Матано-Больцманапри диффузии из постоянного источника в полубесконечное тело, коэффициент диффузии в точке С, — кривой распределения концентрации находят по формуле.

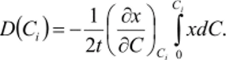
Здесь задача обработки результатов сводится к нахождению произ;

водной в точке °^х ' и интеграла ⁰

При этом экспериментальная кривая С (дг) разбивается по точкам Ах, весь заданный интервал по д: делится пополам и вычисляются площади Si и S₂ (рис.4). Затем из большей площади вычитается малая часть и прибавляется к меньшей. Эта процедура продолжается до тех пор, пока Si и S₂ не станут равны в пределахзаданной точности. В результате этой операции определяют положение плоскости Матано, т. е. хм. Для каждого значения д,.

в котором вычисляют коэффициент диффузии, находят dx _ А* и по.

dC С,-С_й_, формуле трапеции определяют ^xdC- Полученные значения перемножа;

CI.

ют, а результат умножают на ½1.

При xi=J[t) коэффициент диффузии:

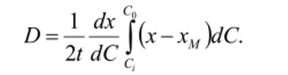aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">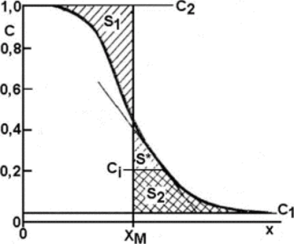

Рис. 4. Распределение концентрации в составном образце.

Для определённой концентрации С, при которой требуется найти D,.

dx_

dC находят из тангенса угла наклона касательной к концентрационному профилю в точке Си Значение интеграла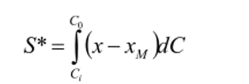

также можно найти графическим интегрированием.