Случайные функции, процессы и потоки случайных событий

Случайная величина в результате опыта принимает одно заранее неизвестное, но единственное значение. Такой подход к изучению случайных явлений в ряде практических задач недостаточен. Часто приходится иметь дело с СВ, непрерывно изменяющимися в процессе опыта.

Примерами их являются: параметры суточных графиков нагрузки потребителей за определенный период времени; изменения располагаемой мощности электростанций, зависящие от метеоусловий и других внешних факторов; изменения спроса мощности и энергии в узлах и в энергосистеме в целом; колебания напряжения в электрической сети; ошибки систем измерения электрических величин; параметры управления режимами ЭЭС; потоки событий, такие, как количество отказов и восстановлений элементов систем энергетики и др.

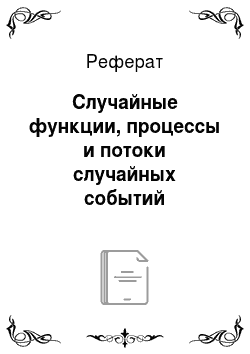
Изменяющиеся в процессе наблюдений (опытов) СВ представляются случайными функциями (СФ), значения которых при каждом значении аргумента являются СВ. Вид, принимаемый СФ в результате опыта, называется реализацией. Если проводится п независимых опытов, возникает семейство реализаций случайной функции X (t) — x_t(t), x₂(/) (рис. 7.19).

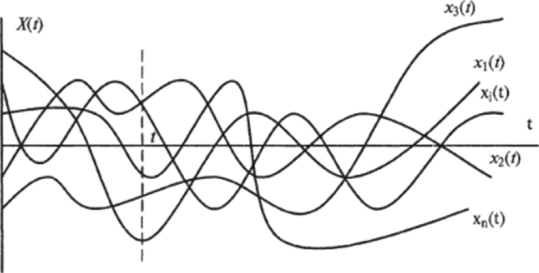
Рис. 7.19. Семейство реа. шзаций х"(1) случайной функции X (t).

Каждая реализация — неслучайная функция. При фиксированном значении аргумента / случайная функция X (t) превращается в СВ, представляемую п значениями, которая называется сечением случайной функции, соответствующим данному /. На практике пользуются числовыми характеристиками СФ, аналогичными числовым характеристикам СВ — математическим ожиданием, дисперсией, корреляционным моментом. В отличие от числовых характеристик СВ, числовые характеристики СФ представляют собой функции.

Математическое ожидание случайной функции X (t) — неслучайная функция m_x(t), которая при значении аргумента / равна математическому ожиданию соответствующего сечения случайной функции m_x(t) = M[X{t). Математическое ожидание СФ — «средняя» функция, около которой варьируются конкретные реализации случайной функции (рис. 7.20).

Рис. 7.20. Математическое ожидание m_x®™ MX (t) случайной функции X (t).

Дисперсией случайной функции X (t) называется неслучайная функция D_x(t), значение которой для каждого / равно дисперсии соответствующего сечения случайной функции D_x(t) = D[X{0. Дисперсия СФ при каждом значении t характеризует разброс возможных реализаций случайной функции относительно среднего — «степень случайности» случайной функции.

Среднее квадратическое отклонение СФ: ст_х (/) = yjD [А (/)].

Хотя математическое ожидание и дисперсия — важные числовые характеристики СФ, для описания особенностей А (/) их недостаточно, поскольку при одинаковых значениях т_х1 (/) = т_х2(/) и D_xl(t)= D_x2(t) (рис. 7.21) не определяется поведение возможных реализаций x,{t).

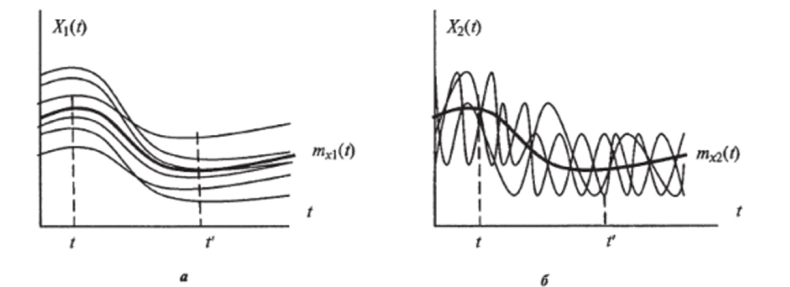
Рис. 7.21. Поведение возможных реализаций x"(t) случайных функций Х(/) и Xj (f).

Для случайной функции X{t) (рис. 7.20,о) характерно плавное, постепенное изменение. Если в точке t одна из ее реализаций хДО приняла значение, выше то с большой вероятностью можно утверждать, что в точке f она примет значение, больше среднего. Следовательно, для X (t) ярко выражена зависимость между се значениями при различных /. Случайная функция АДО (рис. 7.21, б) имеет резко выраженный колебательный характер с быстрым затуханием зависимости между ее значениями по мере увеличения отрезка t, f.

Для описания внутренней структуры СФ вводится корреляционная (автокоре;Ыяционная) функция, характеризующая степень зависимости между сечениями СФ, относящимися к различным t. Две случайные величины x (t) и х (г') в сечениях случайной функции / и /'(см. рис. 7.21) являются зависимыми. При небольших отрезках /, /' величина x{f) принимает значение, близкое к x (t) с относительно большой вероятностью. При увеличении интервала между сечениями t, /' зависимость x (t) и х (/') должна убывать.

Степень их зависимости характеризуется корреляционным моментом, являющимся функцией двух аргументов / и. Следовательно, коррекционной функцией случайной функции X (f) называется неслучайная функция двух аргументов К_х (/,/'), которая при каждой паре значений /, f равна корреляционному моменту соответствующих сечений случайной функции:

где

Если аргументы корреляционной функции совпадают / = /', то она обращается в дисперсию СФ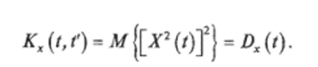

При построении корреляционной функции задаются рядом равноотстоящих значений аргумента и строят корреляционную матрицу системы СВ — таблицу значений для аргументов на плоскости (/,/'). Вместо корреляционной функции К_х (/, t) используют нормированную корреляционную функцию.

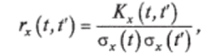
которая представляет собой коэффициент корреляции величин х (/) и x (f).

При определении характеристик случайной функции X (t) рассматривается ряд ее (обычно равноотстоящих) сечений для моментов времени Зарегистрированные значения X (t) заносятся в таблицу, каждая строка которой соответствует конкретной реализации с л у¹! а иной функции, а столбец — сечению (конкретному значению времени) (табл. 7.9).

Таблица 7.9.

Оценки математических ожиданий, дисперсий и средних квадратических отклонений, корреляционных моментов и коэффициентов корреляции сечений СФ находятся по формулам:

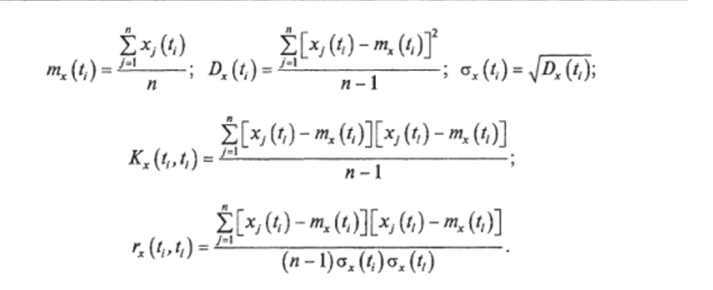
Пример. Потребление электрической энергии промышленным предприятием в течение пяти суток изменялось в соответствии со значениями, представленными в табл. 7.10. Рассматривая потребление электроэнергии как случайный процесс, найти математические ожидания, дисперсии и коэффициенты корреляции для указанных сечений процесса.

Таблица 7.10.

Решение:

а) проведём оценку математического ожидания электропотребления в сечении 1:

Результаты остальных вычислений приведены в табл. 7.11 и представлены нормированной корреляционной матрицей |г_л/|.

Таблица 7.11.

Так как r_tJ = г_и, то матрица ||r_/f/|| заполняется только над главной диагональю, все элементы которой равны 1.

В системах энергетики встречаются случайные функции, имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени. Такие случайные функции называются стационарными случайными процессами.

Случайный процесс — стационарный, если математическое ожидание m_x(t), дисперсия D_x(t) не зависят от t или не меняются при любом сдвиге аргументов, от которых они зависят, по оси Г.

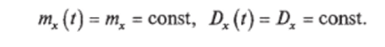
Корреляционная функция стационарного случайного процесса K_x(t, t + т).

зависит нс от положения t первого аргумента на оси абсцисс, а только от промежутка т между первым и втооым аогументами На практике вместо корреляционной функции /Г_х(т) используют нормированную корреляционную функцию.

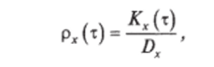
которая представляет собой коэффициент корреляции между сечениями случайного процесса, разделенными интервалом т. Очевидно, что 0) = 1.

Поскольку стационарный случайный процесс протекает однородно во времени, считается, что единственная реализация достаточной продолжительности может служить полной его характеристикой. В этом случае стационарный случайный процесс обладает свойством эргодичности, состоящем в том, что практически каждая его реализация является «полноправным представителем» всей совокупности возможных реализаций.

Одной из иллюстраций случайных процессов является последовательность случайных событий: исправная работа элемента или системы, отказ, восстановление работоспособности, исправная работа и та. Поэтому в теории надежности пользуются понятием потока событий.

Под потоком событий понимается последовательность событий, при которой они происходят одно за другим в случайные моменты времени /. Основными потоками событий, изучаемых в теории надежности, являются потоки отказов и восстановлений. Отказ и восстановление — два противоположных случайных события. Отрезки времени между ними являются СВ, которые также характеризуют вероятность отказа. Наиболее важными характеристиками потока отказов и восстановлений являются математическое ожидание числа отказов (восстановлений) на интервале (0,/), интенсивность отказов (восстановлений), параметр потока отказов.

Простейшим потоком событий называется поток, удовлетворяющий условиям стационарности, отсутствия последействия и ординарности.

Стационарность потока отказов означает, что вероятность появления определенного числа отказов п за некоторый интервал времени не зависит от того, где располагается на оси времени / этот интервал, а зависит только от длительности интервала. Поэтому вероятность возникновения фиксированного числа отказов на заданном интервале времени не зависит от выбора начала отсчета времени, а плотность потока появления отказов постоянна во времени. Следовательно.

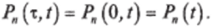
Потоки отказов в период нормальной эксплуатации близки к стационарному, а в период приработки и старения нестационарны.

Отсутствие последействия означает, что вероятность возникновения фиксированного числа отказов на интервале времени (/, t + Л/) не зависит от того, сколько отказов возникло до момента t + Д/. Условие отсутствия последействия выражает взаимную независимость отказов, что определяет независимость протекания потока в непересекаюишхся интервалах времени.

Ординарность потока показывает, что вероятность возникновения двух и более отказов /** за промежуток времени Дt пренебрежимо мала по сравнению с вероятностью возникновения одного отказа.

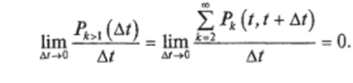
Таким образом, ординарность потока исключает случаи одновременного возникновения нескольких отказов.

Если оборудование или установка состоят из большого числа элементов, каждый из которых может отказать лишь с относительно малой вероятностью, и эти отказы взаимно независимы, что характерно для установок электроэнергетики, суммарный поток отказов считается близким к простейшему. Несмотря на то, что на практике не всегда наблюдается выполнение всех трех условий (стационарность, ординарность, отсутствие последействия), простейший поток служит приближенной физической моделью для широкого круга задач, выдвигаемых требованиями эксплуатации объектов электроэнергетики.

Рассмотрим потоки ординарных событий, различающихся только моментами их появления. Графически поток отказов и восстановлений можно представить в виде бесконечно коротких импульсов при «мгновенном» восстановлении (рис. 7.22, а), либо в виде прямоугольных импульсов при конечном времени восстановления (рис. 7.22, б).

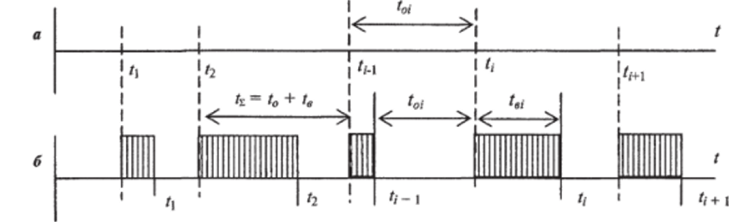
Рис. 7.22. Потоки отказов и восстановлений при нулевом (а) и конечном (6) времени восстановления:

*Ы ~ время непрерывной работы между отказами; 1, — время, затрачиваемое на восстановление; t_l-t₀^Jrt_t — время между отказами

В соответствии с рис. 7.22 величины t₀, t_e, t_i - являются случайными. Число отказов для каждого фиксированного значения / > 0 соответствует N₀(t); число восстановлений при этом N_t (/).

Эмпирическая вероятность отказа за любой отрезок времени /о подсчитывается как отношение суммы всех /о/, меньших То. ^к сумме всех То/, полученных за время наблюдений (испытаний):

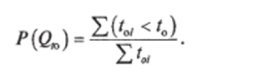
Аналогично определяется эмпирическая вероятность восстановлений за промежуток времени tg.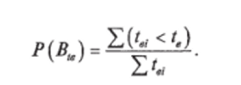

Ряд таких эмпирических оценок даст представление о функциях распределения случайных величин Т₀ и Tg, характеризующих вероятности случайных событий отказа и восстановления. Характеристики функций распределения случайных величин Т₀, Тд и T_Z = T₉ + T_t полностью описывают надежность восстанавливаемых и невосстанавливаемых изделий, объектов и систем с вероятностной точки зрения. Для получения этих характеристик требуется относительно большой объем наблюдений. Поэтому во многих случаях ограничиваются числовыми характеристиками, которые получают на основе эксперимента и которые достаточно полно характеризуют надежность.

Фундаментальное значение в теории надежности имеет функция восстановления H (t)_y которая равна математическому ожиданию числа восстановлений за интервал времени (0, /]: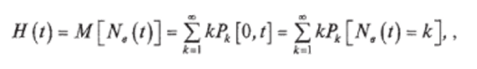

где.

Ру [0/ /]*/*[N_e (f) = k~j — вероятность появления в промежутке [0, t) ровно к восстановлений.

Для процессов с «мгновенным» временем восстановления (см. рис. 7.22, а) функция восстановления обозначается O (f) и называется функцией отказов. Это математическое ожидание числа отказов на интервале [О,/]:

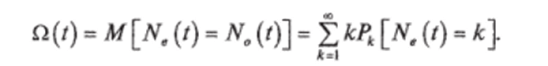
Важной характеристикой потока является мгновенный параметр потока отказов — со (г), определяемый пределом:

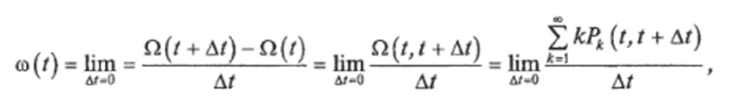
где.

P_k (t, 1 + At) — вероятность появления на промежутке (/, t + Л/) ровно к отказов; ?2(/, t + At) — среднее число отказов на промежутке (t, t + А/).

Параметром потока отказов со (/) называется среднее число отказов восстанавливаемого объекта в малом единичном интервале работы At -> 0 около момента /.

Наработкой называют длительность или объем работы оборудования, измеряемые в часах, километрах, циклах, кубометрах или других единицах.

Понятие «мгновенная интенсивность потока» вводится для нсвосстанавливаемых объектов, которые могут иметь только одно нарушение работоспособного состояния. Классическим примером такого объекта является электрическая лампа.

Интенсивность потока отказов — условная плогность Х (/) распределения наработки невосстанавливаемого объекта до отказа в малом единичном интервале около момента / при условии, что до этого момента отказ не возник:

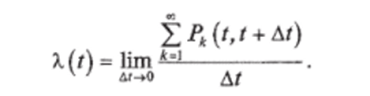
Восстанавливаемые объекты, какими являются ЭЭС и составляющие их элементы, за время эксплуатации могут иметь множество отказов, после которых происходит восстаноштснис работоспособности. Поэтому' для них понятие интенсивности (i) теряет смысл, так как само условие «отказа до момента t не было» не выполняется — отказы были и были после них восстановления работоспособности, после чего объекты продолжали работать.

Использование понятия интенсивности отказов для восстанавливаемых объектов возможно, и его часто используют, но при условии, что объект в определенные периоды эксплуатации рассматривается как невосстанавливасмый (например, в период до первого отказа) или после восстановления работоспособности до следующего отказа. Об этом иногда забывают, что приводит к терминологической путанице [8, 12, 24].

Для ординарных потоков 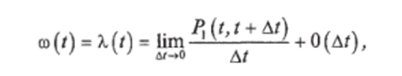где.

Pi (t, t + At) — вероятность появления на промежутке (/,/ + At) одного отказа;

0(ДТ) — условное обозначение бесконечно малой величины более высокого порядка малости, чем Д/.

Для стационарного потока и интенсивность потока X, и параметр потока со не зависят от времени Г. Я,(/) = const; о>(/) = const. Нели поток событий к тому же и ординарный, то о> = X = const.

Ординарные потоки без последействия называются пуассоновскими потоками. Поскольку плотность простейшего потока (среднее число событий в единицу времени) постоянна, вероятность того, что число отказов к на произвольном интервале времени At распределяется по закону Пуассона с постоянным параметром X определится как: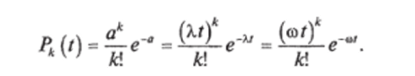

Для стационарного потока а = Xt = о>/. Вероятность отсутствия отказов за время t (к = 0):

Это экспоненциальное распределение, показывающее вероятность безотказной работы R (t).

Вероятность отказа определяется как Следовательно, закон распределения времени безотказной работы Т₀ также экспоненциальный, с параметром М[Т_Ф — 7^ = — = —.

X о Функции Q (t) и P (t) (или R (t)) имеют вид, представленный на рис. 7.23, при условии, что зависимость интенсивности отказов от времени на периоде нормальной эксплуатации соответствует рис. 7.14.

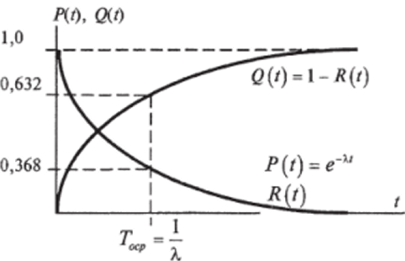
Рис. 7.23. Вероятность откола Q (t) и безотказной работы P (t) при зкспонени, иа.*ьном законе распределения наработки до отказа

Вероятность безотказной работы не зависит от времени предшествующей работы элемента, объекта или изделия, а зависит только от рассматриваемого интервала времени. Это значит, что будущее поведение элемента или объекта не зависит от прошлого, если он в настоящий момент работоспособен. Такое свойство называется характеристическим.

Для объекта с таким свойством закон распределения времени безотказной работы — экспоненциальный, а поток отказов — простейший.

На основе изложенного следует, что для определения характеристик простейшего потока достаточно знать X или со.

Поток восстановлений по аналогии с потоком отказов характеризуется:

• 1) вероятностью восстановления за время г. V (t) = P (T_t < г);
• 2) вероятностью нсвосстановлсния за время г G (t) — 1 — V (t) = Р (Т_в? /);

«о.

3) средним временем восстановления: 7^, = М[Т_в — V (t)dt_y

о.

«ч 1.

4) интенсивностью восстановления: ц = —.

Т

Электроэнергетические установки в большинстве своем относятся к восстанавливаемым техническим системам. После отказа установки или ее оборудования следует восстановление (ремонт).

Под восстановлением понимается обнаружение повреждения или неисправности и их устранение. Случайная величина Т_в — время восстановления — складывается из составляющих:

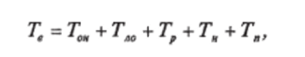
где.

Т_м — время на обнаружение неисправности;

Т_Л0 - время локализации отказа;

Т_р — время на устранение неисправности или ремонт;

Т_м — время наладки после устранения отказа;

Т" — длительность предпусковой проверки.

В общем случае все перечисленные слагаемые являются СВ со своими законами распределения, зависящими от ремонтопригодности, алгоритмов функционирования и правил технического обслуживания.

Закон распределения V (/) СВ Тр для различного оборудования описывется экспоненциальным гамма-распределением, или распределением Вейбулла.

Экспоненциальный закон распределения времени восстановления справедлив при следующих условиях:

• 1) когда восстановление связано с рядом попыток, каждая из которых приводит к необходимому результату с какой-то вероятностью;
• 2) когда плотность распределения времени восстановления убывает с возрастанием аргумента.

Обнаружение неисправности в электротехнической установке осуществляется, как правило, рядом последовательных проверок и удовлетворяет первому условию.

Второму условию соответствует требование быстрого восстановления основной массы отказов. Значительные задержки в восстановлении оборудования энергосистем наблюдаются относительно редко, что подтверждается аварийной статистикой.

Пуассоновские потоки могут быть и нестационарными. Нестационарность потока отказов у отдельных типов электроэнергетического оборудования вызывается наличием периода приработки, когда выявляются скрытые дефекты изготовления и монтажа, наличием старения изоляции, износа и разрегулировки механических частей.

Высоковольтное оборудование имеет сезонную нестационарность, связанную с воздействием гроз, талых вод или гололеда. Для нестационарного пуассоновского потока число событий в интервале времени Д/.

Распределение времени Т между двумя соседними отказами для нестационарного потока не подчиняется показательному закону, определяется видом зависимости Х (/) и расположением на оси t первого отказа.

Отметим, что решение инженерных задач оценки надежности и эффективности объектов и систем электроэнергетики с учетом нестационарное™ потоков отказов и восстановлений — чрезвычайно трудоемкая задача, поскольку возникает необходимость учета множества особенностей их функционирования, связанных с контролем состояния элементов, последействием отказов, возможностью изменения структуры системы, учетом различных видов резервирования.