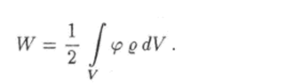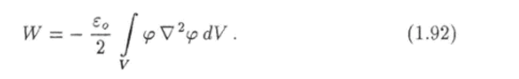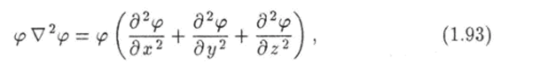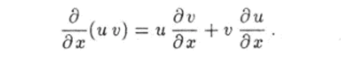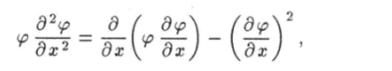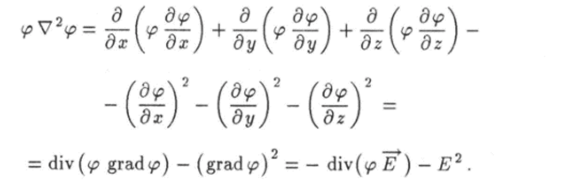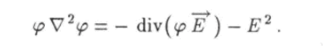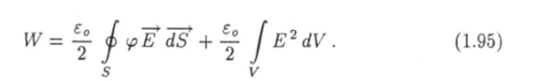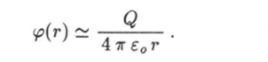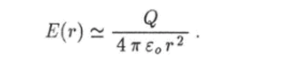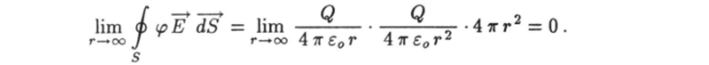Энергия электрического поля

Энергия взаимодействия зарядов, заключенных в объеме V, определяется формулой (1.49)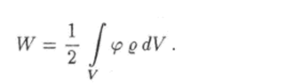

Из уравнения Пуассона (1.73) следует, что объемная плотность заряда выражается через потенциал так:

С учетом этого выражения можно записать Преобразуем подынтегральное выражение.

используя правило дифференцирования произведения функций.

которая позволяет привести выражение (1.93) к виду.

Таким образом, получили тождество.

Преобразуем при помощи этого тождества интеграл (1.92) следующим образом:

По теореме Остроградского — Гаусса интеграл от дивергенции преобразуем в интеграл по поверхности 5, которая ограничивает объем V. Получим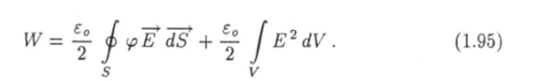

Пусть поверхность 5 является сферой достаточно большого радиуса г и все заряды рассматриваемой системы находятся внутри этой сферы. Согласно формуле (1.81) потенциал любой системы зарядов на больших расстояниях от нее убывает как 1 /г или еще быстрее, если полный заряд системы Q равен нулю. Пусть Q ф 0, тогда.

При этом величина вектора напряженности электрического поля.

Совершая такой предельный переходе равенстве (1.95), приходим к формуле.

где интегрирование производится по всему пространству. Согласно этой формуле энергия системы зарядов равна объемному интегралу от функции Очевидно, что величина есть энергия, содержащаяся в малом объеме dV. Возникает вопрос: какой вид материи является носителем этой энергии? Функция (1.97) определяется только напряженностью Е электрического поля. Поэтому логично предположить, что именно электрическое поле, заполняющее объем dV_} обладает энергией (1.98). В этом случае функция ш (г) есть объемная плотность энергии электрического поля, т. е. энергия поля, заключенная в единичном объеме.

Задача. По формуле (1.96) вычислить энергию электрического поля, создаваемого точечным зарядом Q. Объяснить полученный результат.