Конечномерные представления случайного процесса и разложение Карунена — Лоэва

В этом параграфе мы рассматриваем вопрос о представлении случайных процессов набором стандартных функций. Такое представленное имеет самостоятельное и важное практическое значение. При этом решается ряд проблем: 1) оптимизации, 2) проецирования на конечномерные подпространства из 1²(Т), 3) привлечения геометрических понятий (выражаемых через математические ожидания), связанных с пространством случайных величин, и 4) спектрального представления операторов.

Проблема формулируется просто. Мы хотим найти оптимальный п-мерный базис в L²(T) для представления отдельных реализаций случайного процесса, такой, чтобы норма ошибки в L²(T), усредненная по множеству реализаций, была минимальной. Мы покажем, что для решения этой задачи нужно лишь, чтобы автокорреляционная функция процесса была известна. Эвристически имеется близкая аналогия между этой задачей и задачей отыскания оптимального базиса для класса сигналов, полученных в результате отображения пространства L²(-оо_з оо) компактным оператором. Теперь сигналы задаются своей автокорреляционной функцией. Для полноты аналогии можно считать, что эта функция задает процесс, полученный путем линейной фильтрации (с неизменными во времени параметрами) белого шума.

Здесь не требуется, чтобы оператор фильтрации был компактным, требуется лишь, чтобы он был инвариантным во времени. В этом случае мы получим компактное множество сигналов, рассматривая представления только для ограниченных интервалов времени. Причина такого ограничения связана с тем, что многие важные процессы (например, стационарные) имеют достаточно характерные реализации, ограниченные по времени. Поэтому не имеет смысла проектировать эти реализации на конечномерные подпространства, состоящие из функций, определенных на всей оси времени.

Разложение Карунена — Лоэва

В разложении Карунена — Лоэва отдельные реализации x_w имеют п-мерное представление в виде разложения по функциям времени:

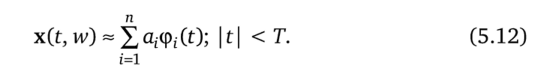
Мы полагаем для удобства, что {ср_г(0} — ортонормированный базис в LK-T, Т), т. е.

П.

Тогда норма ошибки в L²(-T, Т) будет 8_lv = x_lv —? a_t(p,(t).

i=l.

Ошибка принимает минимальное значение для выбранной реализации, если коэффициенты а_г удовлетворяют условию.

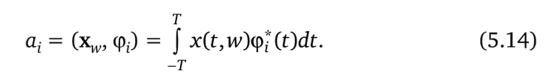
Квадрат нормы минимальной ошибки можно выразить скалярными произведениями:

Заметим, что (в^, e_w) и {аД случайны, это есть реализации соответствующих случайных величин, причем их статистические свойства зависят от выбора базиса {ф,}. Мы попытаемся выбрать п базисных функций {ф,} так, чтобы математическое ожидание случайной величины (b_w, s_lv) было минимальным. Обозначим через /_ф среднее значение квадрата нормы, т. е.

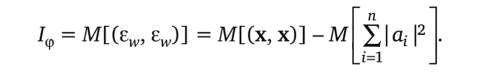
Изменив порядок усреднения и интегрирования, с учетом (5.14) получим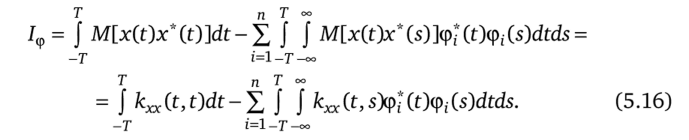

Здесь первое слагаемое не зависит от {ф,}. Поэтому задача состоит в том, чтобы найти п ортогональных функций, максимизирующих величину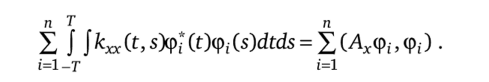

Максимизируемая величина есть сумма квадратичных функционалов. Условия максимума можно выявить, если учесть, что ядром интегрального оператора А_х

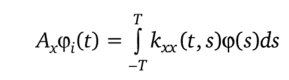
является автокорреляционная функция процесса с конечным средним квадратом.

Это позволяет сделать ряд заключений о свойствах оператора. Можно видеть, что А_х есть оператор: 1) типа Гильберта — Шмидта, 2) самосопряженный и 3) неотрицательно определенный. Свойство 1 следует из квадратичной интегрируемости ядра, что вытекает из ограниченности s) и конечности интервала интегрирования. Свойство 2 следует из симметрии k^it, s) = /c^.(s, t). Для доказательства свойства 3 заметим, что для всякой функции ф (А_хф, ф) = М[ | х, ф |²] >0.

Учитывая указанные свойства, можно заключить следующее.

1. Собственные значения образуют счетную квадратично-суммируемую последовательность. Они вещественны и неотрицательны. Мы можем расположить их в порядке убывания:

2. Ядро может быть представлено равномерно сходящимся рядом по собственным функциям {|/,} оператора А_х:

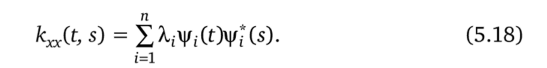
3. Собственные функции могут быть ортонормированы так, что.

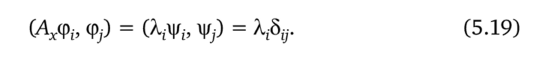
Применив оператор А_х к произвольной системе функций {ф,}, получаем

Мы убедимся в этом, если будем почленно максимизировать выражение в левой части (5.20). Сначала найдем функцию ф_: единичной нормы, которая обращает в максимум квадратичный функционал Gfyp, ф). Учитывая (5.19), возьмем ф_: = ф₁. Далее найдем функцию ф₂, также единичной нормы, такую что она ортогональна к ф_х и тоже дает максимум функционалу Gfyp, ф). Мы приходим к ф₂ = |/₂ ^и> продолжая этот процесс, к ф_?— = |/j для всех i = 1, 2, …, п. Для найденного оптимального базиса формула (5.16) дает.

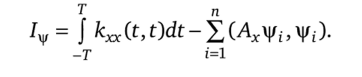
Подставив (5.17) и (5.19), получим далее.

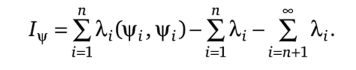
Резюмируя все предыдущее, можно заключить, что п-мерное подпространство в L²(-T, Т), оптимальное для представления реализаций случайного процесса на интервале 111 < Т, натянуто на п собственных функций уравнения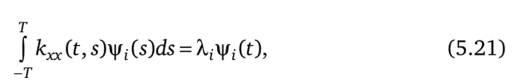

соответствующих п наибольшим собственным значениям Разложение случайного процесса, использующее оптимальный базис,.

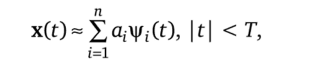
называется разложением Карунена — Лоэва.

Коэффициенты этого разложения есть ортогональные случайные величины, поскольку.

Средний квадрат нормы ошибки есть сумма остальных собственных значений. Этот результат очень важен, так как можно установить, сколько можно выиграть при аппроксимации, если добавить еще несколько членов разложения. Естественно, с увеличением Т собственные значения в общем возрастают и нужно больше членов разложения, чтобы получить приемлемую точность аппроксимации.

Контрольные вопросы

• 1. Зачем необходимо описание случайных процессов?
• 2. Как представляются случайные информационные процессы?
• 3. Что такое пространства случайных сигналов и как они выражаются?
• 4. Объясните роль стационарных случайных процессов в описании сигналов.
• 5. Что характеризуют автокорреляционные функции стационарных случайных процессов?
• 6. Что характеризуют взаимно-корреляционные функции стационарных случайных процессов?
• 7. Поясните роль комплексных и двумерных процессов при анализе сигналов.
• 8. Что характеризуют конечномерные представления случайного процесса в разных пространствах сигналов?