Граничные условия четвертого типа
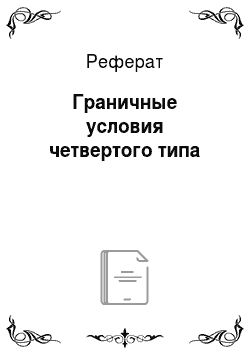
Где i = 1, N, с начальными условиями (4.95) и замыкающими соотношениями (4.91), (4.92). Уравнение (4.105) совпадает с уравнением (4.33), аппроксимированным в граничной ячейке по пространственной координате, при условии, что конвективные потоки через грани приграничной ячейки одинаковы. В этой связи оно обычным образом как и ранее расщепляется для учета конвекции и диффузии с помощью явной схемы… Читать ещё >
Граничные условия четвертого типа (реферат, курсовая, диплом, контрольная)
Для корректной формулировки сеточных граничных условий на входе в канал при докритическом квазистационарном затекании, а также на поверхности горения неподвижного или движущегося заряда, воспользуемся интегро-интерполяционным методом [220] и запишем уравнение баланса, соответствующее обобщенному уравнению (4.24) в приграничной ячейке сетки (см. рис. 4.1). Для этого проинтегрируем уравнение (4.24) по ^ в интервале [^ъ ^2]> полагая, что границы области и соответствуют граням граничных ячеек сетки (см. рис. 4.1).
Si =5 i, i = 0, N;?a=Z, 1, i-l, N-1.
I + — I + ;
2 2.
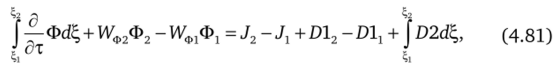
dD.
где J — Г—; индексы 1, 2 соответствуют параметрам на левой и правой.
д?,
грани ячейки сетки. Будем полагать, что преобразование координат.
(4.20) и сетка по ?, (см. рис. 4.1) выбраны так, что = const, 2 = const. Тогда.

Аппроксимируем интегралы по ячейкам сетки, вводя в рассмотрение переменные в приграничных узлах i = 1, N:
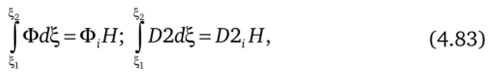
где Н = ft, в начале канала, Н = hN в конце канала. Подставляя (4.82), (4.83) в (4.81), после деления на Н получим.
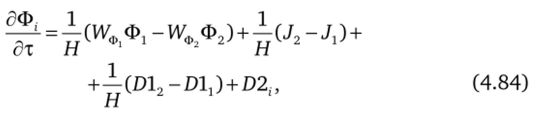
где Ф, 17ф, D, Dl, D2 те же, что и в (4.24).
При рассмотрении поверхности горения полагаем, что она представляет собой плоский фронт, на котором меняется агрегатное состояние вещества заряда, сопровождающееся выделением энергии, который распространяется по заряду со скоростью ил относительно заряда, причем площадь поверхности горения равна Sk, к = 1, 2 (см. рис. 5.1). При этом на поверхности горения выполняются условия.
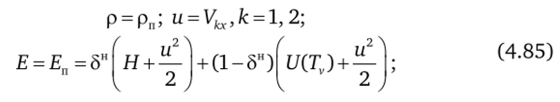
С1п = 1, если продукты сгорания топлива есть первая компонента смеси, С1п = 0 — в противном случае. Полагаем, что величины кинетической энергии турбулентности к'к и диссипации турбулентности ек, к = 1, 2 задаются с помощью соотношений подобных (4.67), (4.68).
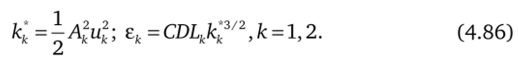
Учтем также, что Ve (скорость сетки относительно неподвижной системы отсчета) и и (скорость среды относительно сетки) в начале канала равны Ve = -ил + Vlx; и = Vljr, а в конце канала равны Ve = ил + V^; и = Vfr. Полагая на горящих поверхностях на концах канала коэффициенты неравномерности уф = 1, получим в силу (4.24).
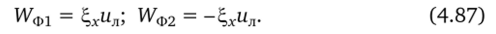
С учетом этого конвективные потоки УУфкФк на горящих поверхностях в начале (к = 1) и конце (/с = 2) канала запишутся 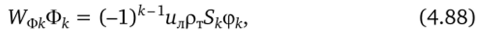
где.
fc = 1, Vfo., ?", С1п, Kk, ek для уравнений (4.24) с номерами 1—6 соответственно; Sk(Zk) — площадь поверхности горения заряда в начале (/с = 1) и в конце (/с = 2) канала.
Система уравнений (4.84), описывающая процесс горения торцевого заряда в приграничной ячейке сетки и истечения газа из этой ячейки дополняется уравнениями (4.89) изменения объема W*0, i = 1, N приграничной ячейки, уравнением изменения величины свода заряда (4.90) и уравнениями состояния (4.91), (4.92), определяющими температуру и давление в ячейке.
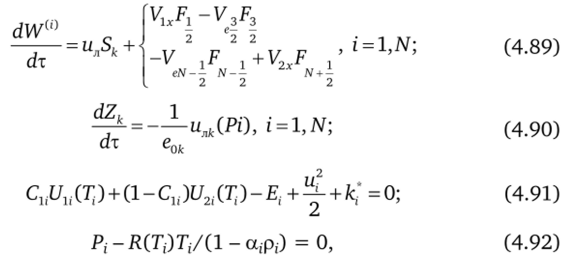
где к = 1, i = 1; к = 2, i = N; Sk(Zk) — площадь поверхности горения; еок — начальная величина свода заряда топлива (см. рис. 5.1). При расчете горения зарядов на подвижных элементах к уравнениям (4.89) — (4.92) добавляются уравнения (5.12)—(5.16), определяющие движение подвижного элемента.
Система уравнений (4.84), (4.88)—(4.92) в начальный период функционирования заряда в канале является жесткой, так как величины слагаемых в правой части (4.84), описывающих горение, намного превосходят таковые описывающие конвекцию. В этой связи уравнение (4.84) расщепляется по физическим процессам таким образом, чтобы отделить расчет горения от расчета конвекции и диффузии. При этом на каждом шаге расчета течения в канале расчет параметров в граничных узлах проводится в три этапа. На первом этапе рассчитывается движение подвижного элемента (ПЭ), несущего заряд. Если заряд закреплен на неподвижном торце, то этот этап обходится и скорость подвижного элемента полагается равной нулю. При расчете движения ПЭ решается система уравнений (4.39)—(4.42). При этом на шаге предиктор используется явная схема Эйлера, а на шаге корректор явная трехслойная схема второго порядка точности по времени [14], [184], [221]. После расчета движения и положения ПЭ на концах канала, рассчитываются параметры адаптирующейся сетки, включая Vem +VV'(')m + 1, где WWm +1 — объем ячейки в момент т + 1 с учетом изменения за счет движения ПЭ,.
+1 — скорость движения сетки, учитывающая движение ПЭ в интервале tm, tm+1. На втором этапе проводится учет горения заряда. При этом решается система уравнений (4.89)—(4.92) и уравнение.
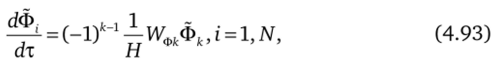
где к = l, i = 1; к = 2, i = N, с учетом (4.86) с начальными условиями.
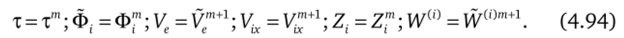
Отметим, что эта система уравнений эквивалентна системе, описывающей горение заряда в замкнутом сосуде. Эта система уравнений аппроксимируется неявной схемой Рунге — Кутта второго порядка точности [14], описанной далее. На третьем этапе проводится учет конвекции и диффузии при течении в канале. При этом решается система уравнений.
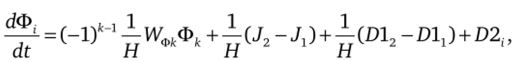
где i = 1, N; к = 2, i = 1; к = 1, i = N, с начальными условиями.
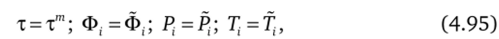
и замыкающими соотношениями (4.91), (4.92). Уравнение (4.94) совпадает с уравнением (4.33), аппроксимированным в граничной ячейке по пространственной координате, при условии, что канал имеет глухой срез. В этой связи оно обычным образом расщепляется для учета конвекции и диффузии с помощью явной схемы (4.39)—(4.42) или явнонеявной схемы (4.43)—(4.46) и включается в общий процесс расчета течения в канале. При этом граничные условия на срезе канала ставятся так же, как и условия на движущейся непроницаемой стенке, описанные в параграфе 4.9.3.
При затекании газа в канал из сосуда-источника система уравнений (4.84) описывает процесс изменения параметров в приграничной ячейке и учитывает приток газа в ячейку из сосуда и отток из нее за счет конвекции в канале. При этом параметры течения на срезе канала связаны с параметрами в сосуде-источнике с помощью формул изэнтропического расширения для газа Дюпре — Абеля (4.70)—(4.75). При этом затекание в канал предполагается докритическим и давление на срезе канала задается равным давлению в прилежащем к срезу узле сетки, а теплофизические свойства газа в источнике замораживаются. Итоговые соотношения для параметров течения на срезе имеют вид.
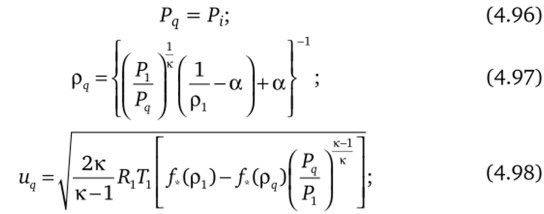
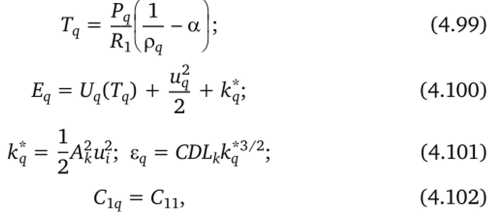
где в начале канала к = 1, i = 1, q = в конце канала к = 2, i = N, 1.
q = N -индексом «1» обозначены параметры в сосуде-источнике.
Эти соотношения позволяют рассчитать конвективные потоки на гранях приграничных ячеек, соответствующих срезам каналов. Однако при таком задании параметров на срезе канала система уравнений (4.84) становится жесткой в период начала затекания газа из сосуда в канал при прорыве мембраны на входе в канал. При этом параметры затекания мгновенно подстраиваются под перепад давлений в источнике и приграничной ячейке, а параметры течения через вторую грань приграничной ячейки развиваются с запаздыванием, обусловленным инерцией разгона газа в ячейке в результате конвекции. Расщепление по физическим процессам проводится аналогично вышеописанному. Вычисления проводятся, как и выше, в три этапа, но на втором этапе в отдельную подсистему выделяются слагаемые правой части (4.84), включающие как конвективный поток, втекающий в ячейку, так и поток, вытекающий из нее, причем первый аппроксимируется неявно, а второй явно. Такое расщепление позволяло ускорить сходимость итераций в этом случае более чем в 10 раз по сравнению с вариантом расщепления, полностью аналогичным вышеописанному для горения на поверхности торцевого заряда. При этом процесс расчета затекания газа в приграничную ячейку аналогичен расчету заполнения проточного сосуда. На втором этапе проводится учет изменения параметров в приграничной ячейке за счет затекания из сосуда и оттока в канал. При этом решается система уравнений (4.89)—(4.92), в которой уравнение (4. 90) сохранено для единообразия алгоритма, но правая часть его полагается равной нулю, и уравнение.
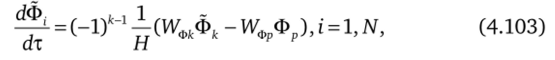
где к = 1, р = 2, i = 1; к = 2, р = 1, t = N. При этом поток на входной грани приграничной ячейки выражается через параметры течения на срезе канала с помощью переменных pq, uq, Tq, Eq, kq, ?q, Ciq и используются начальные условия (4.94). Эта система уравнений аппроксимируется неявной схемой Рунге — Кутта второго порядка точности [14], но поток на выходе в канал аппроксимируется по параметрам течения на предыдущем шаге по времени. На третьем этапе проводится учет влияния Источниковых членов и диффузии на изменение параметров в приграничной ячейке. При этом решается система уравнений.
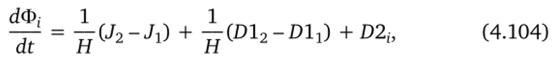
где i = 1, N, с начальными условиями (4.95) и замыкающими соотношениями (4.91), (4.92). Уравнение (4.105) совпадает с уравнением (4.33), аппроксимированным в граничной ячейке по пространственной координате, при условии, что конвективные потоки через грани приграничной ячейки одинаковы. В этой связи оно обычным образом как и ранее расщепляется для учета конвекции и диффузии с помощью явной схемы (4.39)—(4.42) или явно-неявной схемы (4.43)—(4.46) и включается в общий процесс расчета течения в канале. При этом граничные условия на срезе канала ставятся таким образом, чтобы обеспечить обращение в ноль конвективного члена уравнения (4.47) в приграничной ячейке. Этот обеспечивается заданием конвективного потока через грань ячейки, соответствующую срезу канала, равным таковому на второй (внутренней)грани.
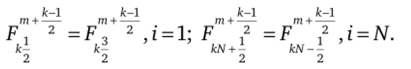
Решение систем уравнений (4.89)—(4.93) или (4.89>—(4.92), (4.104), описывающих процесс горения заряда в приграничной ячейке или затекание в приграничную ячейку из сосуда, на втором шаге расщепления проводится следующим образом. Введем вектор неизвестных — суммарных параметров газовой смеси в ячейке, дополненных величиной свода заряда и температурой и давлением в приграничном узле.
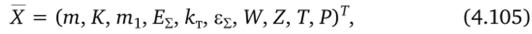
где т — масса газовой смеси в ячейке; К — импульс; тг — масса первой компоненты; Ех — полная энергия газовой смеси; кТ — кинетическая энергия турбулентности; е? — диссипация турбулентности; W — объем ячейки; Z — величина свода заряда; Т — температура; Р — давление. При этом система уравнений горения (4.89)—(4.93) переписывается в виде.
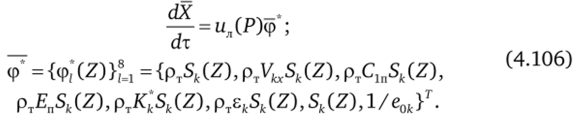
Эта система уравнений на шагах предиктор (j = 1) и корректор (j = 2) аппроксимируется неявной схемой Рунге — Кутта второго порядка точности [14] образует нелинейную алгебраическую систему уравнений для определения неизвестных хт+>/2. При этом используются замыкающие соотношения (4.86) и полагается, что.
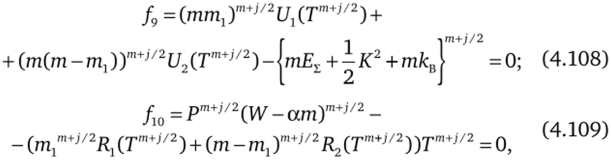
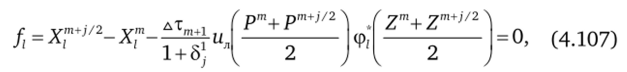
где l = 1, 8, которая в сочетании с уравнениями состояния (4.91),.
(4.92), записанными в виде.
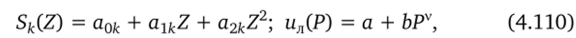
где аок, ахк, а2к, b, v — заданные постоянные.
Система уравнений затекания (4.89)—(4.92), (4.103) переписывается в виде.

где.
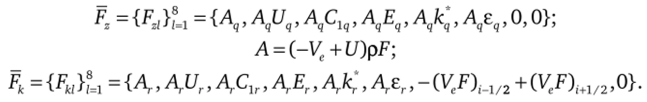
3 1.
Здесь 8, = 1, г = - при i = 1, 5, = -1, г = N — - при i = N; индекс q соответствует параметрам на срезе канала или в отверстии газодинамической связи.
Система уравнений (4.112) на шагах предиктор Q = 1) и корректор (j = 2) аппроксимируется неявной схемой, сочетающей неявную аппроксимацию Рунге — Кутта второго порядка точности [14] для слагаемого XFZ, учитывающего затекание в канал, и явную аппроксимацию слагаемого Fk, учитывающего конвекцию через смежную со срезом канала грань ячейки.
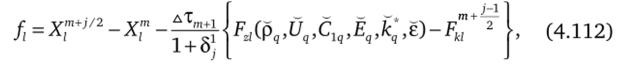
1 m + -.
где ф =—(tpm+(p 2), Z = 1,…, 8, которая замыкается соотношениями.
(4.96)—(4.102) и решается вместе с уравнениями состояния (4.109), (4.110).
Нелинейные системы алгебраических уравнений (4.107)—(4.110) или (4.112), (4.109), (4.110) записываются в виде.
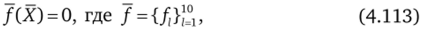
и решается итерационным методом Ньютона [112], [197], причем при расчете итерации Хп +1 решается линейная система уравнений.
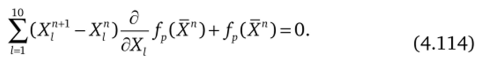
df 110.
Матрица Якоби | |- вычисляется аналитически и имеет следующую структуру.

Выражения коэффициентов через компоненты вектора X опущены ввиду громоздкости. Система уравнений затекания (4.89)—(4.92), (4.104) записывается и решается аналогично, причем матрица Якоби имеет такую же структуру, но дополнительно коэффициенты а18 =.
= а2 8 = <^38 = а48 = а58 = а68 = а78 = а710 = а810 = 0.
Структура матрицы (4.115) позволяет сформулировать простой алгоритм решения системы уравнений (4.114), включающий три шага:
• вычисление коэффициентов расчетных формул.
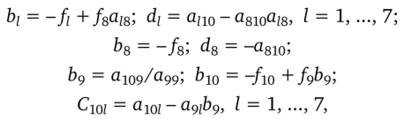
С учеТОМ а102 = <3l04 = а105 = а106 = а96 =
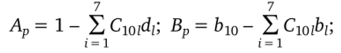
• расчет приращений решения на итерациях.
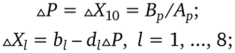
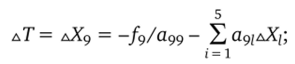
• расчет очередного приближения решения X;m + 1 = X" + дХ(, I = = 1, 10. Отметим, что коэффициент а99, текущее значение теплоемкости газовой смеси при постоянном объеме, всегда отличен от нуля. Расчет компонент вектора Хт +-,/2 позволяет задать значения основных переменных интегрирования для расчета течения в канале в приграничных узлах i =1, N с учетом зависимостей.
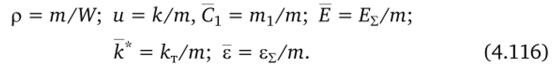
Описанным способом могут быть сформулированы граничные условия во входной ячейке канала, в которой есть как горящий заряд, так и отверстие, связывающее канал с сосудом. Если на конце канала есть только газодинамическая связь со смежным сосудом, расчет может быть упрощен. В этом случае, в силу соотношений (4.96)—(4.102), правые части уравнений (4.113) зависят только от одного параметра Pq — давления на срезе, отождествляемого с давлением в узле ячейки. Введем в рассмотрение целевую функцию.

где/; — невязки уравнений (4.113) на итерациях. Точное решение (4.113) является решением уравнения.

и может быть получено методом итераций Ньютона, в котором производная функции F'(Pq) рассчитывается численно. При этом на итерации п + 1 имеем.
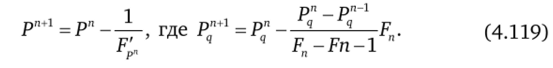
В качестве Pq берется Pq В качестве Pq берется Р/‘+ / рассчитанное при явной аппроксимации Р2; в (4.112).
Описанный способ, наряду с предыдущим, программно реализован в рамках описываемой методики и показал хорошие вычислительные свойства. Для расчета давления во входной ячейке канала при прорыве мембраны на входе требовалось не более 6—8 итераций. При этом начальные невязки уравнений (4.113) уменьшались в 105—106 раз.
Изложенные подходы к расчету поступления газа в канал в квазиодномерном случае позволяют сформулировать методы расчета течений в перфорированных каналах, а также в каналах с горящей газовзвесью.