Динамика вскрытия головной части с произвольным движением разделяющихся тел в пространстве

Рассматривается кассетная головная часть, вскрывающаяся в два этапа. На первом этапе из кассеты после съема оболочки за счет совместного действия инерционных и аэродинамических сил выбрасываются восемь пусковых труб (ПТ), уложенных в кассете между продольными ребрами соосно комплектами по две трубы ПТ1г и ПТ2?, i = 1, 2, 3, 4. На втором этапе из свободно движущихся труб пиродинамически выбрасываются БЭ. Поперечное сечение кассеты представлено на рис. 5.5. В продольном направлении ПТ фиксированы прокладками, вставленными между трубой и днищем кассеты. Радиальное движение переднего торца ПТ ограничено кольцевым выступом, являющимся фрагментом оболочки, фиксированным на переднем днище кассеты. Оболочка снимается с кассеты назад по ходу движения, после чего задние торцы ПТ начинают радиальное движение, а передние упираются в кольцевой выступ в точках D, что обеспечивает разворот ПТ вокруг кромки высту;

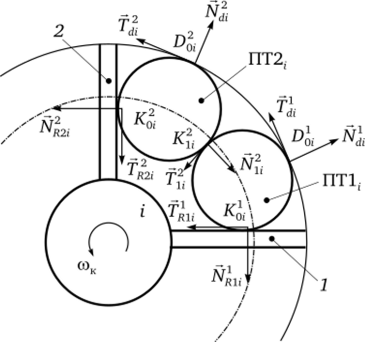
Рис. 5.5. Поперечное сечение кассеты с пусковыми трубами и силы в точках контакта.

па перед отделением их от кассеты. Выход пусковых труб схематично изображен на рис. 5.6.

Процесс съема оболочки с кассеты может быть рассчитан по моделям, описанным в предыдущих разделах. Для расчета отделения ПТ от кассеты ниже сформулирована математическая модель и численный метод ее реализации, учитывающий пространственный характер движения ПТ относительно кассеты в процессе отделения и возможность взаимодействия пусковых труб одного комплекта между собой и с кассетой. Отметим, что в указанной конструкции процессы взаимодействия труб между собой и с элементами конструкции кассеты осуществляются в режиме скольжения. Это обусловлено конструкцией КГЧ и тем фактом, что кориолисовы силы инерции, прижимающие трубу ПТ1_; к ребру 1, недостаточно велики, чтобы обеспечить режим качения без скольжения, что может быть подтверждено элементарными оценками. На рис. 5.7 изображены силы, действующие на пусковую трубу в продольном направлении в точке D контакта с выступом на переднем днище и в точке П контакта с поршнем кассеты. В целом ПТ комплекта.

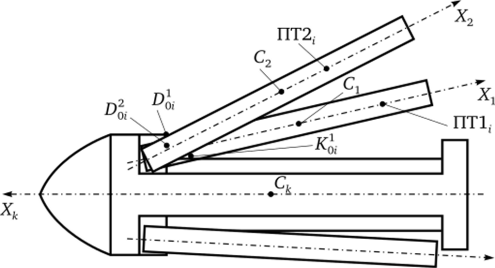
Рис. 5.6. Схема выхода пусковых труб из кассеты.

i = 1-Ммогут взаимодействовать с ребрами кассеты в точках Ко,-, /Cq" с выступом переднего днища в точках dJ, Do,-, с поршнем кассеты в точках П5_;, По, и между собой в точке К^. В этих точках к кассете будут приложены нормальные реакции.

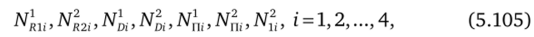
играющие роль неизвестных множителей Лагранжа, которые должны определяться в процессе совместного решения уравнений движения (5.55)—(5.69) и аналитических условий ограничений, связывающих движение ПТ", п — 1, 2, …, 8, и кассеты, как системы взаимодействующих твердых тел. При этом силы трения в точках контакта считаются Кулоновыми и определяются нормальными реакциями и коэффициентами трения скольжения с учетом направления относительной скорости, тел в точках контакта. В процессе отделения ПТ от кассеты контакт с кольцевым выступом переднего днища кассеты в точке D может нарушиться и смениться контактом передней кромки ПТ с поверхностью центральной трубы кассеты. Будем рассматривать эту точку как специфическое положение точки D. Аналогично, после схода задней кромки ПТ с поверхности поршня кассеты, боковая поверхность ПТ может опереться на переднюю кромку поршня. Полученную точку контакта будем рассматривать как специфическую точку П. Факт наличия или отсутствия той или иной точки контакта тел системы устанавливается исходя из геометрии тел и их текущих положений в пространстве. Геометрическое совпадение точек контактирующих тел еще не делает соответствующую одностороннюю связь напряженной. Поэтому расчет каждого шага по времени проводится в два этапа. На первом этапе все связи в точках контакта считаются двусторонними и рассчитываются нормальные реакции в этих точках. На втором этапе в тех точках, которым соответствуют нулевые или отрицательные значения нормальных реакций, эти реакции обнуляются, тела считаются не контактирующими и проводится повторный расчет шага по времени. В целом алгоритм расчета динамики разделения системы включает следующие шаги.

1. Определяются текущие положения точек контакта тел системы и линии действия нормальных реакций в точках контакта.

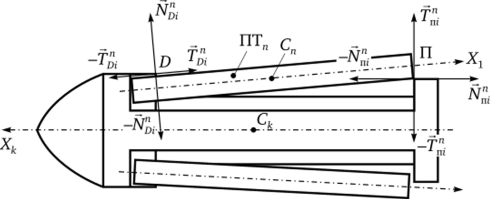
Рис. 5.7. Силы, действующие на отделяющуюся пусковую трубу в осевой плоскости

• 2. Делается очередной шаг интегрирования системы уравнений движения каждого из движущихся тел с одновременным определением нормальных реакций и сил трения в точках контакта с использованием аналитических условий ограничений.
• 3. В случае получения отрицательных нормальных реакций в некоторых точках контакта связи в них считаются ненапряженными и делается повторный расчет с отбрасыванием соответствующих аналитических условий связей и обнулением соответствующих нормальных реакций.

Формализация указанного алгоритма применительно к вышеописанной кассетной головной части приведена ниже. Описание решения геометрической задачи построения точек контакта опущено ввиду громоздкости.

Будем полагать, что в систему тел входит восемь пусковых труб п = = 1, 2, …, 8 и кассета п = 9. С учетом описанных выше возможностей для контакта между телами, нормальные реакции в точках контакта могут быть заданы матрицей контактов N = {N"}¹_n°_{p = 1}, где JV" — сила, приложенная к телу п со стороны тела р. Номер строки матрицы соответствует номеру тела, к которому приложена сила, со стороны тела с номером, равным номеру столбца матрицы. Кассете (тело п = 9), контактирующей с каждой из пусковых труб в двух точках D и П, соответствуют строки и столбцы с номерами 9,10. В силу антисимметричности матрицы N, максимально возможное число неизвестных нормальных реакций — двадцать. Будем нумеровать их в порядке следования в частях строк матрицы N, лежащих выше главной диагонали, для S = 1,…, 20 соответственно.

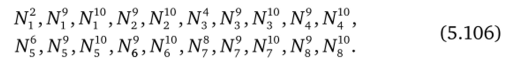
Матрица контактов имеет вид.

Индексы п, соответствующие строке матрицы, и индексы р, соответствующие столбцу, в матрице опущены.

Пусть Rj' — реакция, приложенная со стороны тела п к телу р; п''° — орт внешней нормали к телу п в точке s контакта с телом р; /_п^р — соответствующий коэффициент трения скольжения; V^° — орт, сонаправленный с относительной скоростью тела р относительно тела п в точке контакта.

где Vf_s, — скорости точки контакта тел рипв абсолютной стартовой системе координат QX_rYpZ_r. Выражая силу трения через нормальную реакцию по закону Кулона, можно записать.

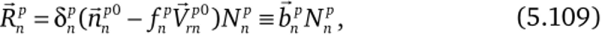
где.

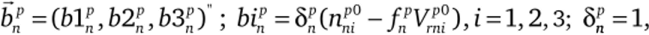
если контакт в точке s существует; 5″ = 0, если контакт в точке s отсутствует.

Уравнения движения каждого из тел системы с номером п = 1, 9.

могут быть записаны в форме (5.55)—(5.69), если вместо главного вектора F₃ и главного момента М_э сил взаимодействия с подвижными элементами подставить главный вектор и главный момент сил взаимодействия тела п со смежными телами. Для проекций векторов на оси i = = 1, 2, 3 системы координат C^(_nY_nZ_n> связанной с телом п, получим с учетом вышесказанного.

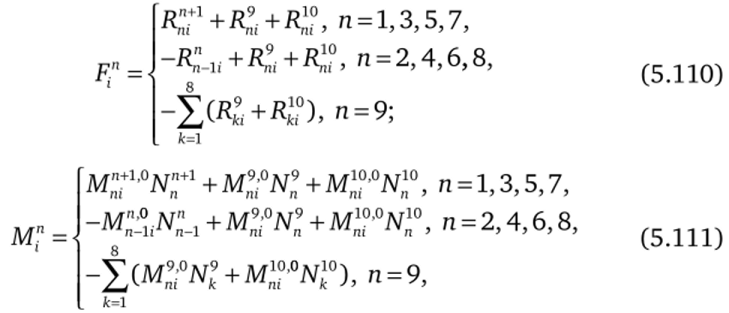
где Я^{Р, 0}=8_п^р[(р_п^Рх(п_п^р0-/_л^рУГ)], Pn — радиус-вектор точки контакта тел пир относительно центра масс С_п тела п.

Выражения (5.110), (5.111) добавляют к неизвестным уравнений (5.55)—(5.69) для тел п = 1, 2, …, 9 двадцать неизвестных (5.107). При этом задача замыкается аналитическими условиями ограничений, выражающими равенство нормальных составляющих абсолютных скоростей точек контакта тел. Для точки s имеем.

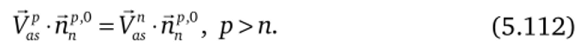
Выражая скорости точек контакта через скорости центров масс контактирующих тел, их угловые скорости и радиусы-векторы точек контакта относительно центров масс тел, запишем (5.112) в виде линейного уравнения.

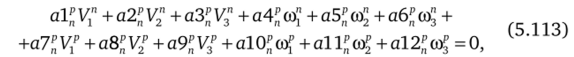
коэффициенты которого определяются текущей геометрией разделяющейся системы. Соотношения (5.113) замыкают систему уравнений для определения кинематических параметров и нормальных реакций в точках взаимодействия. При этом часть из решаемых уравнений являются дифференциальными (5.55)—(5.69), ачасть — алгебраическими (5.113). Для решения этих уравнений построен численный метод, основанный на использовании для аппроксимации дифференциальных уравнений (5.55)—(5.69) неявной схемы второго порядка точности в сочетании с аппроксимацией (5.113) на рассчитываемом временном слое. Это позволяет получить для сеточных значений переменных систему 74 линейных алгебраических уравнений с 74 неизвестными в случае, если все точки контакта реализуются и соответствуют напряженным связям. При отделении тел друг от друга число неизвестных уменьшается до 54 после полного разделения. Алгебраические уравнения решаются методом Гаусса с выбором главного элемента. В процессе дальнейшего свободного движения проверяется возможность реализации соударения тел.

Описанные математические модели и реализующие их алгоритмы позволяют рассчитывать динамику вскрытия на траектории РГЧ СЗО большинства существующих схем. В сочетании с возможностями ППП «МАТМЕХ» [158] для расчета внутрибаллистического процесса в многополостных пиромеханизмах, указанные модели и реализующие их алгоритмы могут составить основу методик проектирования новых РГЧ повышенной эффективности.