Распространение света в одноосных кристаллах

В оптических анизотропных кристаллах, из-за особенности строения их кристаллической решетки, в, п и, соответственно, скорость распространения света зависят от направления распространения и поляризации волны. Проведем мысленный эксперимент: поместим в точку О точечный источник естественного света и построим волновую поверхность через время t (рис. 3.8).

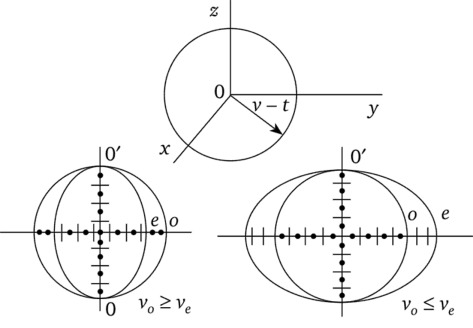
Рис. 3.8.

Если v₀ > v_e (т. е. п₀ < п_е), кристалл называется положительным, пример — кварц.

Если v₀ < v_e (т. е. п₀ > п_е), кристалл называется отрицательным, пример — исландский шпат.

Пользуясь принципом Гюйгенса, рассмотрим распространение света в одноосных отрицательных кристаллах.

Случай 1. Пластинка вырезана перпендикулярно оптической оси (рис. 3.9). В этом случае оба луча (о и е) распространяются в одном направлении с одинаковой скоростью, т. е. не разделяются (как и следовало ожидать, так как луч параллелен оптической оси).

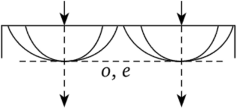
Рис. 3.9.

Случай 2. Пластинка вырезана параллельно оптической оси (рис. 3.10). В этом случае оба луча распространяются в одном направлении, но с разной скоростью. Между этими лучами появляется оптическая разность хода, А = 1(п_е- п₀), где I — толщина пластинки.

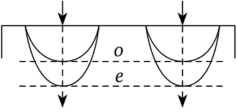
Рис. 3.10.

Случай 3. Пластинка вырезана под углом к оси (рис. 3.11). В этом случае имеет место пространственное разделение лучей. Необыкновенный луч отклоняется от направления падающего света. Оба луча поляризованы во взаимно перпендикулярных плоскостях.

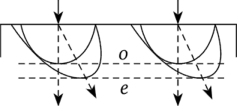
Рис. 3.11.

Поляризационные приборы

Явление двойного лучепреломления используется для изготовления поляризационных призм, фазовых пластинок и других оптических элементов.

1. Поляризационные призмы. Поляризационные призмы состоят из двух или более трехгранных призм из одноосного кристалла с одинаковой или различной ориентацией оптических осей, склеенных между собой прозрачным веществом или разделенных воздушной прослойкой.

Если из призмы выходит только один пучок линейно поляризованного света, то призма называется однолучевой, если оба — то двухлучевой.

Примером однолучевой призмы является призма, изобретенная в 1828 г. шотландским физиком Николем (это первая поляризационная призма) (рис. 3.12). Ее сокращенно называют николем. Обыкновенный луч падает на зазор с канадским бальзамом (оптически менее плотную среду, п₀> п_б> п_е) под углом больше предельного и испытывает полное внутреннее отражение. Необыкновенный же луч проходит насквозь.

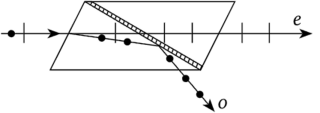
Рис. 3.12.

2. Фазовые пластинки. Рассмотрим случай, когда на кристаллическую пластинку, вырезанную параллельно оптической оси, нормально падает плоская линейно поляризованная волна, в которой вектор Ё ориентирован под углом к оптической оси.

Если совместим ось х с оптической осью, то Ё = Ё_х + Ё_у, и исходную линейно поляризованную волну можно представить как совокупность двух волн, линейно поляризованных в направлениях осей х и у:

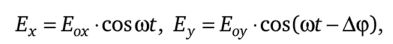
где Аф = ±тп, т — целое число (данное представление аналогично объяснению фигур Лиссажу: при сложении двух взаимно перпендикулярных колебаний, происходящих с одинаковой частотой и сдвигом по фазе, равным тп, получается колебательное движение, т. е. фигура Лиссажу в виде прямой линии, расположенной в соответствующих октантах). Для простоты положим т = 0, тогда.

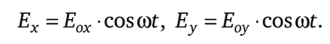
В кристаллической пластинке волна испытывает двойное лучепреломление вследствие чего у компонент Е_х и Е_у появляется дополнительный сдвиг по фазе:

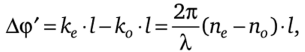
2к, 2п ^.

где к₀ =—п₀, к_е =—п_е — значения волнового вектора для обыкновен;

X X

ной и необыкновенной волн соответственно; X — длина волны в вакууме; I — толщина пластинки.

Таким образом, при выходе из пластинки имеем колебания в виде Совместное решение этих уравнений приводит к уравнению эллипса:

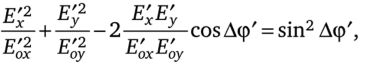
т. е. проекция конца вектора Е' на плоскость, перпендикулярную направлению волны, описывает эллипс колебаний. Такая волна называется эллиптически поляризованной с правым (вращение по часовой стрелке, если смотреть навстречу лучу) или левым (вращение против часовой стрелки) направлением вращения вектора напряженности Ё' во времени.

К

Если Аф' = ±(2т + 1) — и Е'_ох >Е'_оу, то оси эллипса колебаний совпадут с направлением колебаний, и эллипс будет вытянут вдоль оси х

и

(рис. 3.13). ЕслиЕ'* =Е'_оу при Аф' = ±(2т + 1)—, эллипс колебаний вырождается в окружность. Такая волна называется циркулярно поляризованной (или поляризованной по кругу) с левым или правым направлением вращения вектора напряженности. При Дф' = (2т + 1) л уравнение Е'.

эллипса колебаний вырождается в уравнение прямой: Е' = ±——?', т. е.

/7'.

_{w ы} -'-'ОХ волна становится линейно поляризованной.

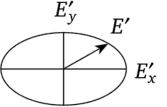
Рис 3.13.

Таким образом, поляризованный свет можно представить как совокупность двух компонент, линейно поляризованных во взаимно перпендикулярных плоскостях, накладывающихся друг на друга с определенным сдвигом по фазе Дф'. При изменении Дф' эллиптически поляризованная волна может быть преобразована в линейно поляризованную, линейно поляризованная в циркулярно поляризованную и наоборот.

Пластинка, вносящая между перпендикулярными компонентами.

К

добавочный сдвиг по фазе 8ф = (2т +1)—, что соответствует добавочной.

X

оптической разности хода Д = (2т + 1)—, называется фазовой пластинкой в четверть длины волны. Аналогично, пластинка, вносящая допол;

X

нительную оптическую разность хода, А = (2т +1) — (или 8ф = (2т +1)л),.

называется фазовой пластинкой в полволны.

С помощью пластинки в Х/4 линейно поляризованный свет можно превратить в эллиптически или циркулярно поляризованный. Пластинка же в Х/2 не изменяет вид поляризации линейно поляризованного света, только поворачивает плоскость поляризации на угол 2а (рис. 3.14). В частности, если ос = 45°, то плоскость поляризации повернется на 90°.

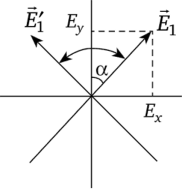
Рис. 3.14.

Действие пластинки в четверть волны используется для анализа эллиптически и циркулярно поляризованного света, так как с помощью одного анализатора (поляроида, призм Николя) нельзя отличить эллиптически поляризованный свет от частично поляризованного света, а циркулярно поляризованный от естественного света. Однако если перед анализатором поместить кристаллическую пластинку в А/4, на частично поляризованный и естественный свет эта пластинка не окажет никакого влияния, а эллиптически поляризованный свет (если одна из осей эллипса колебаний параллельна оптической оси пластинки Х/4) и циркулярно поляризованный свет превратятся в плоско поляризованный, в чем легко убедиться по выполнению закона Малюса.