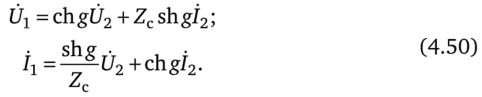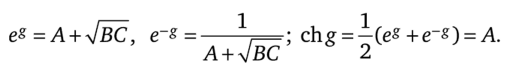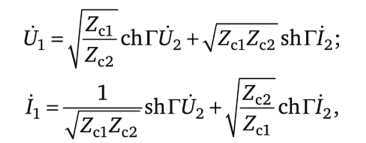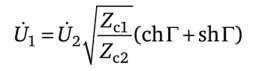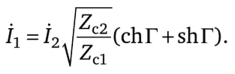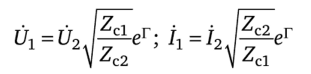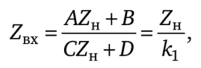Уравнения четырехполюсника, записанные через гиперболические функции

Для симметричного четырехполюсника Л-форму уравнений (4.1) и (4.2) записывают иногда через гиперболические функции от аргумента g, полагая А = D = chg, В = Z_cshg, С = shg/Z_c. При этом AD — ВС = = ch²g — sh²g = 1 и.

Убедимся в справедливости замены А на chg:

Форму записи через гиперболические функции используют, например, в теории фильтров (см. гл. 5).

Для несимметричного четырехполюсника уравнения через гиперболические функции запишем следующим образом:

где Г — мера передачи; chr = J~AD; shT = [ВС.

Если несимметричный взаимный четырехполюсник нагружен на Z_c2,.

ТО й₂ = ^2^с2^:

и.

Имея в виду, что е^г = chr + shr, получим.

Мера передачи Г = а' + jb' = In (-JaD + у/вС). Если четырехполюсник симметричный, то Z_cl = Z_c2, D = А, Г = g. Так как _лJz_cl /Z_c2 = фА/D, то передача по напряжению для несимметричного взаимного четырехполюсника, нагруженного на ^с2> составляет.

^1п{г^=1п + In (л/ AD + yjВС).

и передача по току ln^- = In— + ln (VAD + VbC).

I₂ A

Конвертор и инвертор сопротивления

Если у невзаимного четырехполюсника В = С = 0 и он нагружен на зажимах pq на сопротивление Z_H, то входное сопротивление со стороны зажимов тп

где к_г = D/А, т. е. четырехполюсник преобразует (конвертирует) сопротивление Z_H в сопротивление Z_H//c₁. Коэффициент называют коэффициентом конвертирования. Если А и D имеют одинаковые знаки, то Z_BX

имеет тот же знак, что и Z_H (конвертор положительного сопротивления), если разные, то знак Z_BX противоположен знаку Z_H (конвертор отрицательного сопротивления).

Если у конвертора А = 1, то к_х = D; й_г = й₂; Д = kj₂. В этом случае конвертор называют идеальным конвертором с преобразованием тока (при неизменном напряжении).

Если у конвертора D = 1, то = 1 /А; U₁=U₂/k_l;i_l=i₂. Такой конвертор называют идеальным конвертором с преобразованием напряжения.

У конвертора есть Н- и G-матрицы, но отсутствуют Zи У-матрицы.

Если у невзаимного четырехполюсника А = D = 0, то Z_BX = B/(CZ_H) и четырехполюсник называют инвертором сопротивления, а В/С = к₂ — коэффициентом инвертирования.

Если В и С имеют одинаковые знаки, то Z_BX = 1/Z_H (инвертор положительного сопротивления), если знаки у В и С разные, то Z_BX = -1/Z_H (инвертор отрицательного сопротивления).

У идеального инвертора входное сопротивление не зависит от того, к каким зажимам (pq или тп) подключена нагрузка.

У инвертора есть Уи Z-матрицы, но отсутствуют Н- и G-матрицы.