Круговая диаграмма напряжения четырехполюсника

Пусть напряжение й₁ на входе четырехполюсника на рис. 4.2, а неизменно по модулю, фазе и частоте, а нагрузка Z₂ = z₂e^² на выходе его изменяется только по модулю, так что характеризующий ее угол Ф₂ остается постоянным. В этом случае для тока /₂, напряжения й₂, тока могут быть построены круговые диаграммы. Сначала рассмотрим круговую диаграмму тока /₂. С этой целью схему четырехполюсника (см. рис. 4.2, а), исключая нагрузку Z₂, заменим активным двухполюсником и по методу эквивалентного генератора найдем ток /₂ в ветви pq:

где U_pqx — напряжение между точками р и q при размыкании ветви pq; Z_BX pq =?_2ке^;(р2к — входное сопротивление по отношению к зажимам pq при короткозамкнутых зажимах тп (в схеме на рис. 4.2, а к зажимам тп присоединен источник ЭДС). Разделив числитель и знаменатель правой части (4.74) на Z_Bxpq и учтя, что U_pqx /Z_2k =/_2к, где /_2к — ток короткозамкнутой ветви pq, получим.

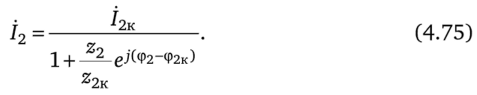
Из уравнения (4.75) следует, что вектор тока /₂ скользит по дуге окружности, хордой которой является ток /_2к.

Построим круговую диаграмму тока i₁ на входе четырехполюсника. Из предыдущего (см. формулу (2.25)) известно, что при изменении сопротивления в одной из ветвей линейной электрической цепи два тока в любых двух ветвях этой цепи связаны соотношением 1_т = а + Ы_п. Следовательно, ток i₁ может быть линейно выражен через ток /₂:

Определим коэффициенты а и Ь. Если ветвь pq разомкнута, то /₂ = О и 1_г = i_lx. При этом из (4.76) найдем.

Если ветвь pq короткозамкнутая, то /₂ = 4к и = 7_1к. Поэтому.

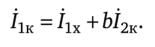
Отсюда.

Подставив (4.75), (4.77) и (4.78) в (4.76), получим.

Уравнение (4.79) свидетельствует о том, что геометрическим местом концов вектора тока также является дуга окружности. Хордой ее является разность /_1к — /_1х; вектор /_1х смещает начало отсчета.

Аналогичным образом строят круговую диаграмму напряжения. Так. если в какой-то схеме изменяется по модулю сопротивление Z₂ = z₂ew* в одной, например второй, ветви, то для напряжения на участке ab этой схемы можно записать выражение, аналогичное (4.79):

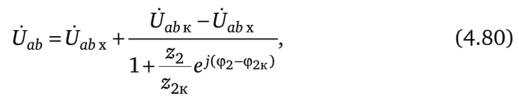
где й_аь_х — напряжение на зажимах ab при z₂ = °о; Й_аЬк — напряжение на зажимах ab при z₂= 0; Z_2k = z_2Ke№^2к — выходное сопротивление схемы относительно зажимов, к которым присоединено сопротивление Z₂.

Формула (4.80) выведена на основании выражения U_ab =а₁+ и (4.74).

Пример 55.

Построить круговую диаграмму тока Д схемы (рис. 4.24, а), в которой Х_с= 5 Ом; R = 5 Ом; Ё = 100 В. Нагрузкой четырехполюсника является индуктивное сопротивление^, которое может изменяться от 0 до.

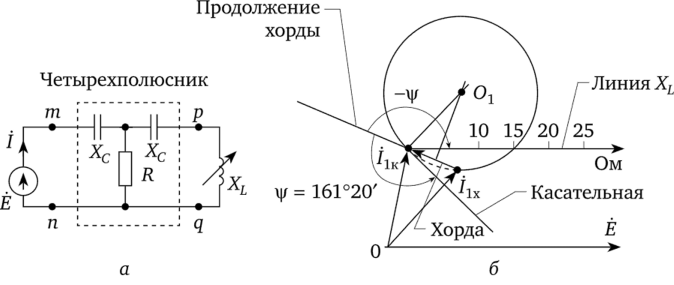
Рис. 4.24.

Решение. Найдем ток холостого хода при разомкнутой выходной ветви:

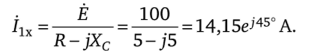
Определим ток короткого замыкания при коротком замыкании нагрузки:

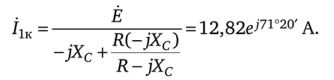
Рассчитаем входное сопротивление Z_2k со стороны зажимов pq при коротком замыкании зажимов тп:

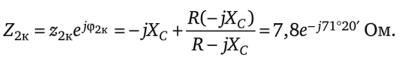
Следовательно, ср_2к = -71°20'. Угол |/ = ср₂ — ф_2к = 90° - (-71°20') = 161°20'.

Круговая диаграмма тока Д построена на рис. 4.24, б. Хордой окружности является разность ДкД_х. Угол i > 0, поэтому для определения положения касательной он отложен от продолжения хорды против часовой стрелки. Диаграмма носит несколько необычный характер: рабочая часть дуги занимает почти целую окружность.

Для определения положения конца вектора Д из конца вектора/_1х через точку на линии X_L, соответствующую заданному значению X_L, проводят прямую до пересечения с рабочей частью дуги окружности. ПриХ_ь= 5 Ом ток опережает ЭДС Ё на 90°.