Расчет методом интегрируемой нелинейной аппроксимации

Данный метод основан на аппроксимации характеристики нелинейного элемента такой нелинейной функцией, которая, во-первых, достаточно точно отображает его характеристику в предполагаемом интервале перемещения изображающей точки по ней и, во-вторых (и это главное), дает возможность точно проинтегрировать уравнение в известных функциях.

Ценность метода заключается в том, что в результате интегрирования получают зависимость исследуемой величины от времени и всех параметров схемы.

Метод применим к дифференциальным уравнениям первого порядка, а также к уравнениям, сводящимся к уравнениям первого порядка путем замены переменных.

Пример 161.

Определить закон нарастания во времени тока при замыкании ключа в схеме на рис. 16.2, а. Зависимость тока от потокосцепления |/ выражена формулой i = к1^л. В схеме нулевые начальные условия.

Решение. Из уравнения цепи ^- + Ri = U следует, что dt = Вынесем из знаменателя множитель R и заменим i на i = к1^л:

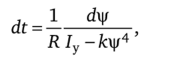
где I_y = U/R.

Обозначим /_у = а² и заменим к/⁴ на)/f; di на / у/к. В результате получим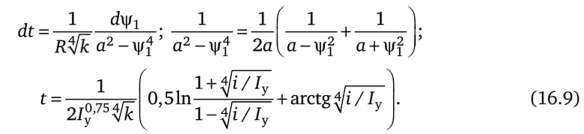

С помощью (16.9) можно определить время, которое необходимо, чтобы отношение i/I_y достигло заданного значения.

Расчет методом кусочно-линейной аппроксимации

При расчете этим методом осуществляется замена характеристики нелинейного элемента отрезками прямых линий, что позволяет перейти от нелинейного дифференциального уравнения к нескольким линейным уравнениям, отличающимся друг от друга лишь значениями коэффициентов.

Каждое из линейных уравнений справедливо для того интервала времени, в течение которого рабочая точка перемещается по соответствующему линеаризованному участку. Метод применим к цепям, содержащим источники постоянной и (или) синусоидальной ЭДС, а также к цепям первого и более высоких порядков.

Для сложных нелинейных цепей с источником (источниками) синусоидальной ЭДС основная трудность расчета данным методом заключается в определении постоянных интегрирования, исходя из законов коммутации и времени работы на каждом линейном участке. В сложных цепях неизвестные находят обычно из трансцендентных уравнений, часто применяют ЭВМ. Впервые идея этого метода была высказана российским физиком Н. Д. Папалекси в 1912 г.

Рассмотрим основные этапы расчета на простейшем примере.

Пример 162.

Конденсатор емкостью С заряжается через HP от источника постоянного напряжения U (рис. 16.3, а). Определить закон изменения тока в цепи при зарядке.

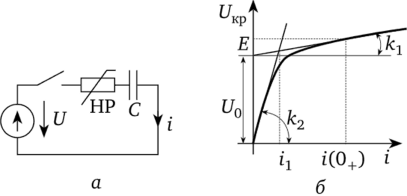
Рис. 16.3.

Решение. ВАХ HP заменим двумя отрезками прямых линий (рис. 16.3, б). Пусть на участке от i = 0 до i = ij u_HP = k₂i, где u_HP — напряжение на нелинейном резисторе; к₂ — коэффициент. На участке i > u_HP = U₀+ fcp.

Размерность коэффициентов fcj и k₂ соответствует размерности сопротив;

ления. В уравнение цепи и_с + u_HP = U вместо и_с подставим — J idt, заменим и_нр для первого участка на U₀ + /ср, а для второго — на k₂i.

При зарядке конденсатора ток постепенно уменьшается от максимального значения до нуля. Поэтому изображающая точка перемещается сначала по первому участку, а затем по второму.

Для первого участка — J idt + U₀ + k_xi = Е; для второго — J idt + k₂i = Е.

Для первого участка i = i_np + i_CB = 0 + А_хе~^^к iO.

Постоянную интегрирования А] найдем из начального условия: t-0,u_c- 0. Поэтому U₀ + /c₁i (0₊) = Е и г (0₊) =А_г = (ЕU₀)/k_x. Следовательно, при работе на первом участке.

Пусть при t = t_x ток i = ij. Подставим в (16.10) i_x вместо i и t_x вместо t и решим полученное уравнение относительно t_x:

При работе на втором участке i = A₂e~^^t~^t^^/^^k2^c причем А_г = i_x.