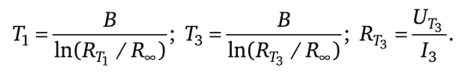Метод интегральных уравнений

От нелинейного дифференциального уравнения можно перейти к интегральному, используя одну из форм записи интеграла Дюамеля. Поясним идею этого перехода. Решение линейного дифференциального уравнения, например уравнения.

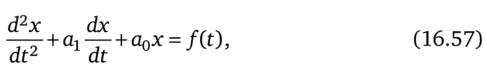
может быть записано в виде.

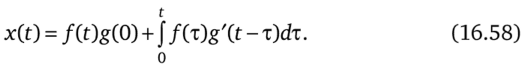
Под g (t) понимают переходную проводимость либо переходную функцию, в зависимости от того, чем является х по отношению к вынуждающей силе ДО; g (t) определим как решение (16.57) при ДО = 1.

Если исходное уравнение нелинейно, например:

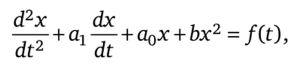
то нелинейный член Ъх² можно перенести в правую часть и рассматривать как внутреннюю вынуждающую силу:

Используя (16.58), запишем решение уравнения (16.59):

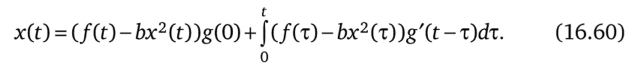
Переходная функция g (t) определяется по линейной части исходного нелинейного дифференциального уравнения при воздействии на нее 1(0. Уравнение (16.60) является интегральным уравнением по типу Вольтерра второго рода. Его можно решать методом последовательных приближений, полагая х₀(0 = х (0) и пользуясь таким соотношением для к-го приближения:

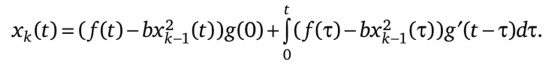
Метод имеет смысл применять только в том случае, когда процесс последовательных приближений является сходящимся.

Пример 165.

Решить уравнение — + х² = 1 при х (0) = 0.

Решение. Для определения g (t) на линейную часть системы воздействуем dx

единичным напряжением: — = 1; g (t) = t; g'(t) = 1; g (0) = 0; g'(t — т) = 1. Запи;

dt

сываем рекуррентное соотношение: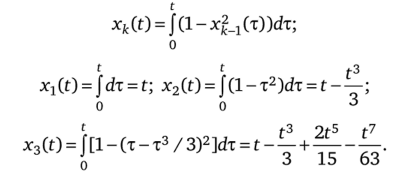

Переходные процессы в цепях с терморезисторами

Методику рассмотрим на примере схемы (рис. 16.6, а). Переходный процесс вызван замыканием ключа К. Полагаем, что температура окружающей среды 0 неизменна. ВАХ термистора при температуре 0 представлена на рис. 16.6, б кривой а. Установившийся режим до коммутации определяется точкой 1, после коммутации — точкой 3. Сразу после коммутации сопротивление термистора (он обладает большой постоянной времени) остается равным его сопротивлению до комму;

и_т

тации R_Tl = —^L. При коммутации изображающая точка скачком пере;

h

мещается из положения 1 в положение 2. После этого она по некоторой траектории перемещается из 2 в 3. Режим в точке 3 будем полагать устойчивым (в [24, § 3.10] разобрано, как исследовать устойчивость этого режима). Переходный процесс описывается уравнением теплового баланса.

^ ^dT

где С_т—теплота, идущая на увеличение теплосодержания тела.

cLt

термистора; С_т — удельная теплоемкость; Т — среднеобъемная абсолютная температура тела термистора; к (Т — 0) — теплота, отдаваемая в окружающее пространство; I²R_T— теплота, выделяемая в термисторе.

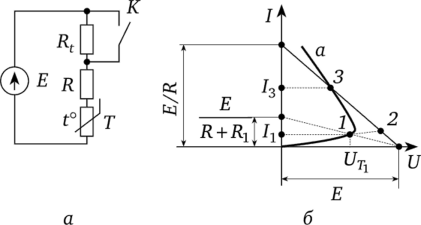
Рис. 16.6.

Полагаем, что за время переходного процесса к и С_т практически неизменны. Сопротивление термистора R_T = R^e^⁷ (см., напри;

АЕ

мер, [24]); R^— сопротивление термистора при Т —" со; в =-, где.

2 к-у

АЕ — усредненная энергия активации; к_г — постоянная Больцмана. Например, для термистора ММТ-1 В = 4600к и R_oa = 5,5 Ом. Из уравнения (16.61) следует, что

Здесь.

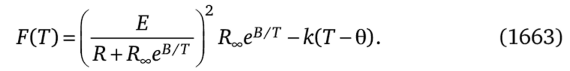
Верхний предел интеграла в (16.63) изменяется от до Т₃: