Свойства статистических оценок

Выше мы обращали внимание на то, что статистический взгляд на вещи подразумевает наличие «двух миров»: мира «истинных» характеристик исследуемых объектов (генеральных совокупностей) и мира оценок этих характеристик, сделанных на основе выборочных совокупностей, причем последние являются лишь приближениями к первым. Сло;

во «приближение», однако, не слишком точное; требуется система понятий и мер, с помощью которых мы могли бы более детально анализировать соответствие между реальностью и полученными статистическими оценками. Ключевыми свойствами последних, характеризующими их соответствие истинным параметрам, являются несмещенность, эффективность и состоятельность.

Для прояснения их смысла начнем с упражнения, являющегося логическим продолжением упражнения 3.4. Нам будет удобнее работать не с исходной случайной величиной («=СЛЧИС»), а с переменной, обладающей значительно большим средним и дисперсией.

Упражнение 3.6

• 1. В таблице упражнения 3.4 определим к = 100, Ь = 0. Теперь переменная У задана функцией У = ЮОЛ', где X — равномерно распределенная случайная величина, колеблющаяся в интервале [0, 1] (функция «=СЧИСЛ»).
• 2. Сохраните оценки среднего, дисперсии и стандартного отклонения для 10 реализаций У Для этого после каждого пересчета копируйте числа в ячейках Е2, Р2 и в2 в новые ячейки, используя опцию «Специальная вставка — значения» (рис. 3.31).

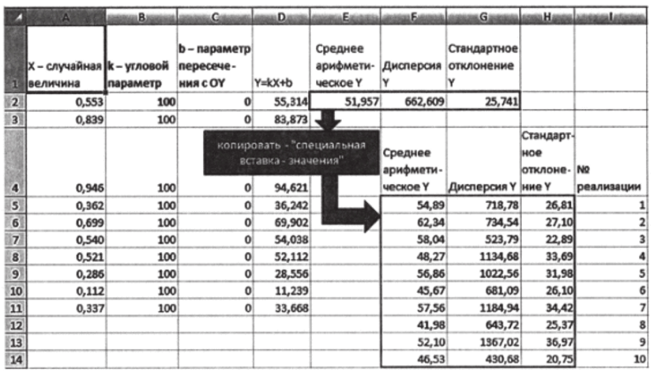
Рис. 3.3/

Таким образом, мы рассчитываем оценки параметров для десяти выборок из генеральной совокупности. Конкретные наблюдения в каждой выборке (реализации) принимают разные значения, это обусловлено случайной составляющей нашей модели. Соответственно, оценки среднего, стандартного отклонения и дисперсии для каждой выборки, которые мы имеем в таблице, также различаются. Оценки параметров сами являются случайными величинами в том смысле, что содержат чисто случайную составляющую. Тем не менее, поскольку выборки извлечены из одной и той же совокупности, оценки параметров должны отражать ее закономерные характеристики, приближаться к ним.

3. Найдем «истинные» (справедливые для генеральной совокупности в целом) значения математического ожидания, теоретической дисперсии и теоретического стандартного отклонения. Так как линейное преобразование сохраняет закон распределения, величина У распределена равномерно, как и Л', функцией которой она является. Для равномерного закона справедливы формулы математического ожидания (3.28) и дисперсии (3.29). Исходная величина X колеблется в интервале от 0 до 1. Следовательно:

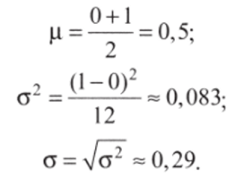
В п. 1 мы осуществили линейное преобразование У = ЮОЛ'. Значит, в соответствии со свойствами линейных преобразований:

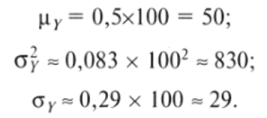
Таковы теоретические параметры распределения нашей величины. Сравните их с оценками, полученными в п. 2. В целом, оценки колеблются «вокруг» истинных значений: для каждой реализации они или несколько ниже, или несколько выше. Это важнейший признак несмещенности статистической оценки. Несмещенная оценка находится около истинного значения параметра, с равной вероятностью отклоняясь в большую и меньшую сторону, завышая и занижая истинное значение. Другими словами, истинные значения являются центрами распределений оценок (рис 3.32а). Несмещенная оценка включает в себя только случайную ошибку; смещение в оценке предполагает систематическое завышение или занижение истинного значения (рис. 3.32б). В этом случае мы имеем дело с систематической ошибкой.

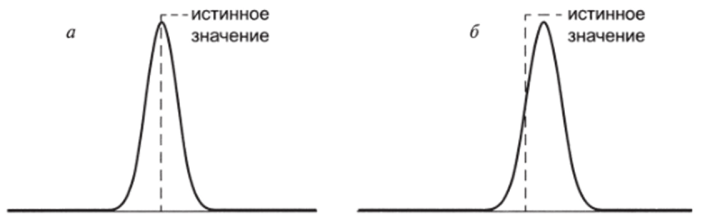
Рис. 3.32. а) Несмещенная оценка; б) смещенная оценка Простой пример смещенной оценки из области политики связан с фальсификациями выборов. Пусть X — некоторый «истинный» уровень электоральной поддержки какойто определенной политической партии, X — официальный результат голосования (представляющий собой — в замысле — оценку истинного уровня поддержки). Если выборы проводятся честно, оценка X будет представлять собой комбинацию истинного значения X и случайной ошибки:

При этом е может принимать как положительные, так и отрицательные значения; официальный результат с равной вероятностью может оказаться как несколько выше, так и несколько ниже «истинного». Модель (3.40) — модель несмещенной оценки результата выборов. Если же имеют место фальсификации, модель изменится таким образом:

где у — систематическое смещение оценки. Если фальсификации производятся в пользу исследуемой партии, этот параметр будет положительным и мы будем получать систематически завышенные оценки результата голосования.

Если фальсификации производятся в пользу другой партии, параметр смешения будет отрицательным и оценки — систематически заниженными. Отметим, что систематические ошибки представляют собой основную угрозу валидности измерений.

Так как оценки являются случайными величинами, обладающими распределениями, для них можно, в свою очередь, рассчитать параметры распределений.

Упражнение 3.7.

1. Рассчитайте среднее, дисперсию и стандартное отклонение для оценок, полученных в п. 2 упражнения 3.6 (рис. 3.33).

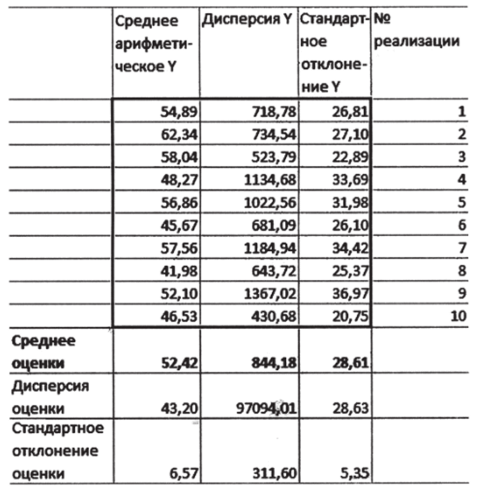
Рис. з.зз

Теперь посмотрим, что будет происходить с увеличением объема выборки:

2. Увеличьте объем выборки до 50 наблюдений. Технически это делается достаточно просто: выделите строку с функциями и параметрами, поставьте курсор в правый нижний угол до появления «крестика» и растяните до 51 строки. Затем измените функции для расчета параметров (рис. 3.34).

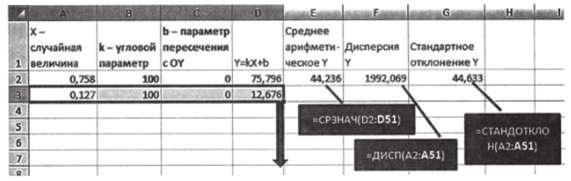
Рис. 3.34.

• 3. Сохраните значения среднего, дисперсии и стандартного отклонения для 10 выборок (реализаций). Действуйте так же, как в предыдущем упражнении.
• 4. Рассчитайте средние, дисперсию и стандартное отклонение для оценок по 10 выборкам, полученным на предыдущем этапе (рис. 3.35).

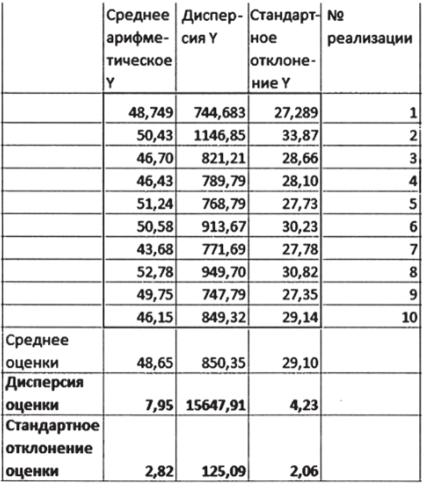
Рис. 3.35

5. Сравните дисперсии и стандартные отклонения оценок, полученных для выборки из 10 наблюдений, с соответствующими показателями для выборок из 50 наблюдений. Для данного примера — см. табл. 3.14.

Таблица 3.14

Очевидно, с увеличением объема выборки (числа наблюдений) разброс оценок уменьшается. Это — ключевой признак состоятельности оценки.

Еще один очень важный момент, связанный с увеличением объема выборки, касается закона распределения оценок параметров. Возьмем выборку из равномерно распределенной генеральной совокупности объемом 50 наблюдений (п = 50). Будем рассчитывать среднее по выборке для 50 ее реализаций, другими словами — для 50 разных выборок одной и той же генеральной совокупности, каждый раз сохраняя результат. Таким образом, у нас получится 50 средних арифметических значений (читатель может проделать все это как дополнительное самостоятельное упражнение, правда, весьма утомительное).

Теперь построим гистограмму распределения полученных средних (рис. 3.36).

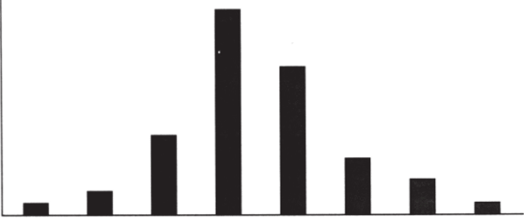
Рис. 3.36.

Получившееся распределение подчиняется нормальному закону, хотя выборки извлекались из равномерно распределенной генеральной совокупности! Более того, при достаточно большом объеме выборки (п > 30) распределение выборочных средних будет описываться нормальным законом независимо от того, как распределена исходная генеральная совокупность. При этом чем больше объем выборки, тем лучше колокол Гаусса будет описывать распределение средних. Это положение доказывается одной из фундаментальных статистических теорем — центральной предельной теоремой. Доказательство мы здесь приводить не будем, для нас важнее некоторые практические следствия из этой теоремы. В частности, центральная предельная теорема позволяет рассчитать стандартное отклонение выборочных средних, которое получило название стандартной ошибки среднего:

где о у — стандартная ошибка среднего, о — стандартное отклонение генеральной совокупности, п — объем выборки.

Стандартная ошибка среднего показывает, насколько оценка центра распределения колеблется вокруг истинного значения. Другими словами, это мера того, насколько в среднем мы ошибаемся при оценке центральной тенденции. Ошибка будет тем больше, чем а) сильнее колебания переменной и б) меньше объем выборки.

Например, мы рассчитываем среднее количество членов местной партийной организации на основе 49 наблюдений; стандартное отклонение составляет 133 человека. Полученное нами среднее арифметическое — 540 человек. Насколько эта оценка точна? Чтобы ответить на этот вопрос, воспользуемся формулой (3.42):

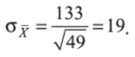
Таким образом, полученная нами по выборке оценка средней численности партийной организации отклоняется от истинного параметра генеральной совокупности в среднем на 19 человек. При увеличении объема выборки до 1000.

стандартная ошибка среднего сократится до 4 человек. При увеличении стандартного отклонения генеральной совокупности до 500 человек средняя ошибка среднего увеличится до 71 человека.

Вернемся к несмещенности и состоятельности оценок. Первая характеристика, напомним, отражает степень совпадения центра выборочных средних с центром генеральной совокупности, вторая — сходимость оценок к некоторому предельному значению. Если оценка является одновременно несмещенной и состоятельной, с увеличением числа наблюдений она будет сходиться (стремиться) к истинному значению параметра. К сожалению, такое бывает далеко не всегда; несмещенность и состоятельность «не привязаны» друг к другу. Точнее, если оценка несмещенная, она всегда состоятельна; но если оценка состоятельна, она не обязательно является несмещенной. Схематично это можно проиллюстрировать следующим образом (рис. 3.37а, б).

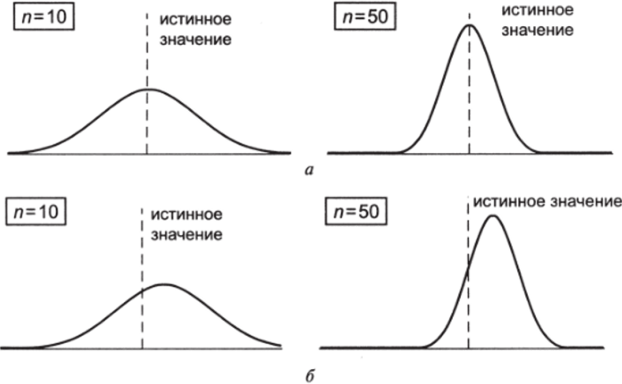
Рис. 3.37. а) Состоятельная и несмещенная оценка; 6) состоятельная и смещенная оценка Этот рисунок иллюстрирует состоятельность оценки — как ее способность сходиться к некоторому числу с увеличением объема выборки; но совсем не факт, что это некоторое число является именно тем истинным значением, которое вы ищете.

Эффективность представляет собой относительную характеристику — она предназначена для сравнения разных способов оценивания. Эффективной среди других оценок является та оценка, которая обладает наименьшей дисперсией. Стремясь к эффективности, мы хотим получить оценку, чье распределение максимально «сжато» вокруг истинного параметра.

Поясним это на следующем примере. Выше рассматривался один способ оценивания центра случайной величины — среднее арифметическое. Однако это далеко не единственный способ оценить среднее значение; более того, это далеко не единственный несмещенный способ.

Сконструируем альтернативную меру положения центра распределения. Для простоты возьмем минимальный объем выборки — два наблюдения (Л^-, и Х₇). Процедура расчета среднего арифметического придает равные веса обоим наблюдениям, они «вносят одинаковый вклад» в итоговую оценку. Это становится понятным в следующей записи;

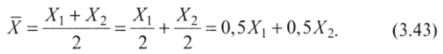
Теперь изменим веса отдельных наблюдений, сохранив неизменной их сумму. Пусть «вклад» первого наблюдения составляет 0,9, второго — 0,1. Мы получили следующую оценку среднего значения (обозначим ее Л"):

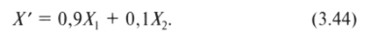
Проверим ее свойства.

Упражнение 3.8

• 1. Присвойте столбцу А1 название «XI», столбцу В1 — название «Х2»; они будут содержать наблюдения. Чтобы их сгенерировать, вновь воспользуемся функцией «=СЛЧИС». Как и в предыдущем упражнении, более наглядной будет «крупномасштабная шкала», поэтому вновь осуществим линейное преобразование. В ячейки А2 и В2 введите функцию «=СЛЧИС ()*100».
• 2. Столбец С зарезервируем за обычным средним арифметическим: в ячейку С1 введите соответствующее название столбца, в ячейку С2 — функцию «=СРЗНАЧ (А2:В2)».

• 3. В столбцах О и Е определим веса XI и Х2 соответственно. В первой строке укажите название «вес XI», «вес Х2», в ячейке Г)2 поставьте 0,9, в ячейке Е2 — 0.1.
• 4. В столбце И рассчитаем оценку X' по формуле (3.44). Введем в ячейку Я2 функцию «=02*А2+Е2*В2».
• 5. Растяните ячейки А2-Е2 до строки 11. Теперь мы имеем 10 выборок случайной величины X и соответствующие средние.
• 6. Рассчитайте среднее арифметическое и стандартное отклонение для столбца С; таким образом будут получены параметры оценок среднего арифметического. То же самое сделайте для оценок в столбце X' (рис. 3.38).

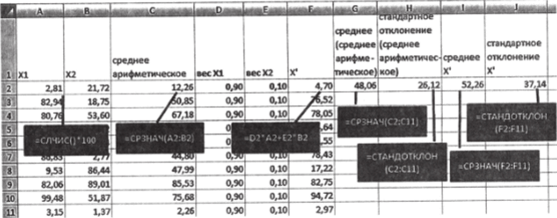
Рис. 3.38

Попробуйте разные реализации этой модели и посмотрите, как ведут себя среднее и разброс оценок X и X'. Обратите внимание, что средние значения для обоих способов оценивания колеблются вокруг истинного среднего — 50. Следовательно, обе оценки являются несмещенными. Отметим, что оценки типа X' с любыми весами будут несмещенными до тех пор, пока сумма весов равна единице. Поэтому кроме среднего арифметического существует, вообще говоря, бесконечное число несмещенных оценок центра распределения. Почему же мы пользуемся, как правило, именно средним арифметическим?

Чтобы ответить на этот вопрос, обратите внимание на разброс оценок X и А". Стандартное отклонение среднего арифметического будет, как правило, существенно меньше, чем стандартное отклонение оценки с неравными ве;

сами^[1]. Другими словами, среднее арифметическое является более эффективной оценкой центра распределения, чем любая оценка типа X' (см. рис. 3.39а и б).

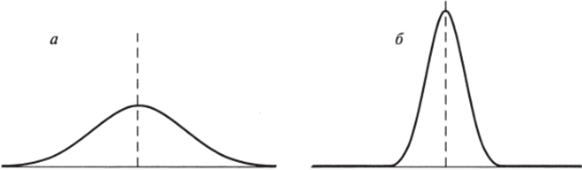
Рис. 3.39. а) Менее эффективная оценка; 6) более эффективная оценка В примере выше мы рассматривали две несмещенные оценки центра распределения, различающиеся по эффективности. Здесь очевидно, что более эффективная оценка предпочтительней. Однако в реальной исследовательской работе возникают ситуации, когда приходится делать более сложный выбор: между эффективной, но смещенной оценкой и несмещенной, но неэффективной (см. рис. 3.40а и б).

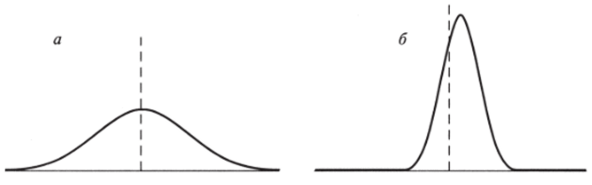
Рис. 3.40. а) Несмещенная и неэффективная оценка; б) смешенная и эффективная оценка В некотором абстрактном статистическом смысле несмещенность представляется более важным свойством оценки, так как она отражает отсутствие систематических ошибок. Эффективность же представляет собой меру подверженности инструмента оценки случайным ошибкам. В то же время смещенная оценка на рис. 3.405 будет почти всегда давать результаты, близкие к истинному значению, тогда как в несмещенном и неэффективном случае отклонение от него может быть очень значительным. Поэтому, если для исследователя приемлемы малые ошибки, но неприемлемы большие, следует выбрать более эффективную оценку, пожертвовав несмещенностью.

Литература

Бродский Я.С. Статистика. Вероятность. Комбинаторика. М., 2008. С. 118−178.

Доннелли Р. Статистика. М., 2006. С. 77—116.

Доугерти К. Введение в эконометрику. М., 2010. С. 3—42. Ибрагимов Н., Суслов В., Талышева А. Эконометрия. Ч. 1: Введение в социально-экономическую статистику. Новосибирск, 2005. Раздел 1.5.

Кремер Н.Ш. Теория вероятностей и математическая статистика. М., 2007. С. 16−61, 87−133.

Gill J. Essential Mathematics for Political and Social Research. Cambridge; N.Y., 2006. P. 330—361.

Keohane R, King G., Verba S. Designing Social Inquiry. Princeton (NJ), 1994. P. 55−63.

Интернет-ресурсы.

Statistical Data Mining Tutorials: Probability for Data Miners, http:// www.autonlab.org/tutorials/prob.htmI; Probability Density Functions. http://www.autonlab.org/tutorials/pdf.html.

Clayton State University, School of business. Electronic Textbook on Business Statistics: Measurement, http://business.clayton.edu/arjomand/ book/sbk06.htm; Frequency Distributions, http://business.clayton.edu/ aijomand/book/sbk07.htm; http://business.clayton.edu/aijomand/book/ sbk08. htm; http://business.clayton.edu/aijomand/book/sbklO.htm; http:// business.clayton.edu/aijomand/book/sbkl l.htm.

• [1] Математическое доказательство этого факта приведено в: Доугерти К.

  Введение

  в эконометрику. Изд. 3-е. М., 2010. С. 25−26.