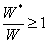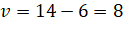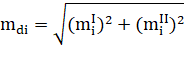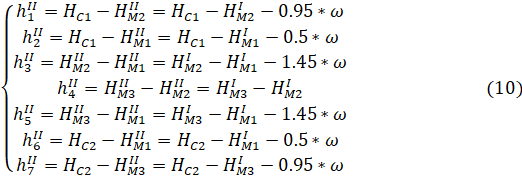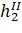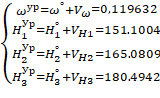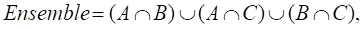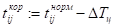Бесконечно малые и бесконечно большие функции

Определение 1. Функция называется бесконечно малой функцией (бесконечно малой) при, если .

Определение 2. Функция называется бесконечно большой функцией (бесконечно большой) при, если .

Замечание. Бесконечно малая функция не всегда принимает малые значения так же, как и бесконечно большая функция может принимать и небольшие значения. Более того, одна и та же функция может быть и бесконечно малой и бесконечно большой. Так функция является бесконечно малой при, так как. Эта же функция является бесконечно большой при, поскольку. Однако, являясь бесконечно большой при, эта функция принимает малые значения при больших значениях, например при, она равна .

Ясно также и то, что если называется бесконечно малой функцией при, то — бесконечно большая при. Аналогично, бесконечно малая при .

Свойства бесконечно малых (функций)

1. Сумма двух бесконечно малых — есть бесконечно малая.

Доказательство. Даны две бесконечно малые, при. Из второго определения предела функции следует, что.

.

.

причем чем меньше, тем меньше и .

Очевидно, найдутся такие, при которых.

.

и если, то при выполняются оба неравенства и. Из неравенства следует, что.

.

то есть, что требовалось доказать.

Следствие. Сумма конечного числа бесконечно малых — есть бесконечно малая.

2. Бесконечно малая, умноженная на конечное число остается бесконечно малой.

Доказательство. Пусть, а конечное число. Из определения бесконечно малой следует.

.

тогда найдется такое при (при), что.

.

Поскольку, имеем.

Другими словами. Свойство доказано.

3. Произведение бесконечно малых также бесконечно малая. По сути это свойство следует из предыдущего.

Необходимость. Пусть и докажем, что бесконечно малая при. Из второго определения предела имеем.

.

но, следовательно,.

.

следовательно, бесконечно малая.

Достаточность. Имеем, причем, нужно доказать, что. Из следует и поскольку, имеем.

.

Доказано.