Двухшаговый метод оценивания

Прежде чем проводить описанный выше первый шаг данного метода, необходимо вычислить параметр, который мы будем считать независимым от времени. Таким образом, де-факто данный подход будет трехшаговым.

В отличие от работы Diebold F.X., Li C. (2006) мы не можем приравнять данный параметр какому-либо наперед заданному числу, поскольку мы не имеем априорной информации о том, как должна в теории вести себя кривая рассматриваемых спредов, кроме того, что в случае нормальной ситуацией с валютной ликвидностью все ее составляющие будут близки к нулю. Однако мы можем считать, что параметр лежит в диапазоне от 1 до 180 (диапазон срочности спредов), поскольку его значение должно соответствовать такой срочности спреда, при которой изгиб кривой будет максимален.

Вначале для каждого момента времени мы можем с помощью нелинейного метода наименьших квадратов оценить все параметры уравнения (1):

.

, ,.

.

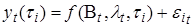
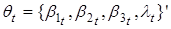
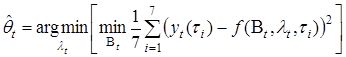
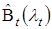
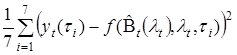
далее для параметра на интервале от 1 до 180 строится сетка, на которой для каждого значения данного параметра оценивается с помощью МНК и вычисляется целевое значение. Из всех значений выбирается то, для которого целевое значение наименьшее.

Ниже приведены статистики для оцененного параметра :

Таблица 5.

Таким образом, выберем медиану параметра равную 23 в качестве значения данного параметра независимого от времени. Теперь с помощью обычного МНК мы оценим. Смысл оценивания данных параметров заново заключается в том, что мы хотим получить ряды этих ненаблюдаемых величин для их последующего анализа и построения моделей на их основе. Для этой цели данные параметры должны порождаться одной и той же моделью в каждый момент времени, следовательно, параметр должен быть фиксированным.

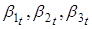
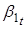
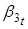
Для параметров существуют приближения, которые можно рассчитать из данных по спредам. Так приближением параметра в нашем случае будет являться спред срочность полгода, поскольку он ближе всего к долгосрочному уровню спреда. Приближением параметра, отвечающего за наклон кривой, будет являться разница между overnigth basis, взятого с обратным знаком и спреда срочностью пологода. В качестве приближения параметра, который отвечает за изгиб кривой, мы выберем удвоенное значение спреда сроком 1 месяц минус сумма значений спредов на полгода и 1 день (overnigth basis с обратным знаком). Статистики по оцененным параметрам, их приближения и самим спредам, а также графики приведены ниже:

Таблица 6.

Графики 6,7,8.

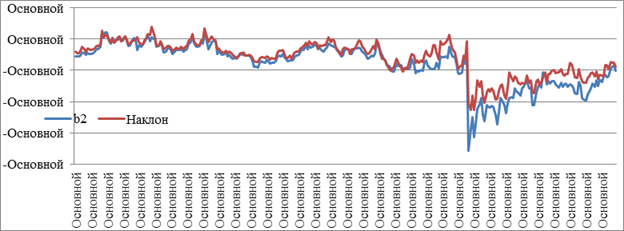
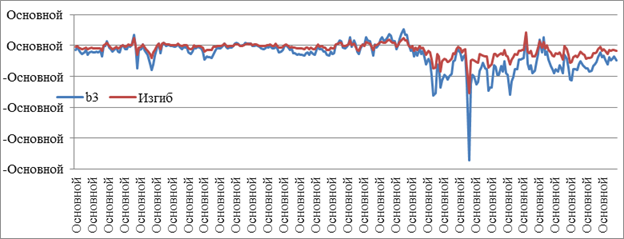
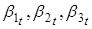
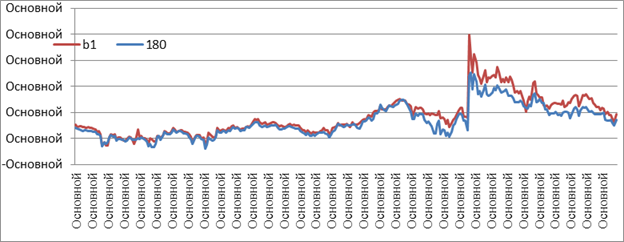
Как видно из данных таблицы 6 и графиков, приведенных выше, оцененные параметры в целом достаточно хорошо соответствует их приближениям. Однако в меньшей степени это справедливо для, что может свидетельствовать о целесообразности рассмотрения двухпараметрической модели Нельсона-Сигеля (за исключением параметра), включающей только первый и второй члены уравнения (1). Выбросы на трех графиках происходящие в начале января 2015 г. обусловлены тем фактом, что рассматриваемая выборка не включает декабрь 2014 г. В связи с этим также может иметь смысл строить модели отдельно по данным 2014 и 2015 годов.

Качество аппроксимации кривой спредов моделью Нельсона-Сигеля является достаточно неплохим. В таблице 7 представлены средние значения и стандартные отклонения остатков модели в зависимости от срочности, выраженные в базисных пунктах.

Таблица 7.

Как видно из данной таблицы кривая аппроксимируется достаточно хорошо, при этом наилучшим образом приближаются ее «ближний» и «дальний» концы, а хуже всего — спред на 1 месяц.

Теперь рассмотрим VAR (1) процесс для параметров :

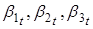
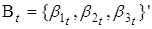
где ,.

— единичная матрица 3×3. Результаты представлены ниже:

Таблица 8.

Корни характеричтического характеричтического уравнения матрицы лежат внутри единичного круга, поэтому данный VAR (1) процесс является стационарным.

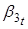
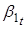
В таблице 7 в скобках указана t-статистика, жирным курсивом выделены коэффициенты значимые на 10% уровне значимости, просто жирным — на 5%, жирным и желтым — на 1%. Таким образом, только для параметра все коэффициенты в той или иной степени являются значимыми, для параметра коэффициент при первом лаге параметра также является значимым, но лишь на 5% уровне.

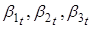
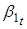
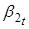
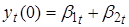
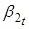
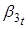
Для того чтобы моделировать зависимость ненаблюдаемых состояний — от чистого кредита, нужно добавить независимую переменную в VAR (1) процесс. Однако прежде чем это сделать, мы можем выдвинуть гипотезы о влиянии данного регрессора на ненаблюдаемые параметры на основе рассмотренной динамики спредов ставок по МБК и ставок по валютным свопам. Увеличение чистого кредита должно приводить к снижению долгосрочного уровня спредов — параметр. Напротив, оно должно оказывать повышательное воздействие на параметр — наклон кривой спредов. По мере роста чистого кредита в 2015 г. происходило сближение «ближнего» конца кривой спредов и «дальнего». Напомним формулу для мгновенной ставки из уравнения (1):. Следовательно, при сближении и параметр должен стремиться к нулю. Однако, как следует их графика 7, данный параметр, как правило, имеет отрицательное значение, поскольку «дальние» спреды обычно выше «ближних». Следовательно, по мере роста чистого кредита параметр также увеличивался (уменьшался в абсолютном значении). Что касается параметра, то исходя из динамики спредов, трудно сделать предположение о том, как чистый кредит будет влиять на изгиб кривой. Де-факто параметр мы используем для лучшей аппроксимации кривой спредов и не придаем ему в данной работе содержательного экономического смысла.

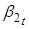
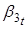
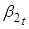
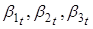
В уравнениях для параметров и на 1% уровне значимости значимыми являются только первые лаги данных параметров. В уравнении для значимым на 1% уровне является также первый лаг параметра. Однако, поскольку ключевыми для нашего исследования являются параметры и, в уравнениях для которых значимы только их первые лаги, то мы будем рассматривать в VAR (1) процесс в спецификации с диаганольной матрицей. То есть, мы будем предполагать, что динамика ненаблюдаемых состояний зависит лишь от их собственных первых лагов. По сути мы будем иметь дело с тремя AR (1) процессами для параметров. Тогда для того чтобы оценить влияние чистого кредита на данные параметра рассмотрим следующую модель:

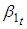
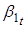
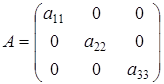
,(5).

Оценим ее параметры с помощью МНК как по всей совокупности наблюдений, так и отдельно по 2014 и 2015 гг.

Таблица 9.

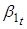
Оцененные значения коэффициентов, приведенные в таблице 9 в целом соответствуют высказанным ранее предположениям. Чистый кредит отрицательно влияет на параметр и положительно на, при этом значение оценки коэффициента по модулю выше, чем значение оценки коэффициента. Это означает, что по мере роста/снижения чистого кредита «дальний» конец кривой спредов будет уменьшаться/увеличиваться быстрее, чем «ближний», что подтверждается на практике: в мае 2014 г. первыми начали возрастать спреды срочностью полгода, тогда как overnight basis оставался стабилен. Кроме того, санкции воздействовали, прежде всего, на привлечение валютной ликвидности на длительные сроки, поэтому «дальний» конец кривой спредов должен был сильнее реагировать на возникновения дефицита валютной ликвидности.

Влияние чистого кредита на параметр прослеживается, только если оценивать модель (5) на всей выборке, и с большими оговорками — на данных 2014 г. При оценивания данной модели на выборке 2015 г. влияние чистого кредита на оказывается незначимым. Тем не менее, как уже было сказано ранее, проблемы в этом нет, поскольку параметр служит лишь для лучшей аппроксимации кривой спредов моделью Нельсона-Сигеля.