Совместимость системы линейных уравнений. 
Действия с векторами

Задача 1.

матрица векторный алгебра уравнение Дана система линейных уравнений. Доказать ее совместность и решить двумя способами:

• а) методом Крамера;
• б) средствами матричного исчисления.

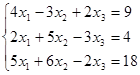
Решение.

Исследуем систему на совместность:

Воспользуемся теоремой Кронекера-Капелли, для этого найдем ранг расширенной матрицы системы и ранг матрицы системы.

Приведем расширенную матрицу системы к ступенчатому виду методом элементарных преобразований, и определим количество ненулевых строк в матрице.

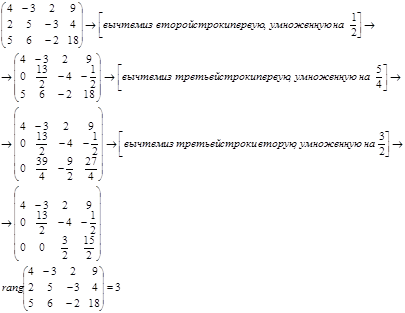
Приведем матрицу системы к ступенчатому виду методом элементарных преобразований, и определим количество ненулевых строк в матрице.

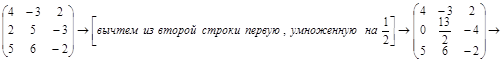
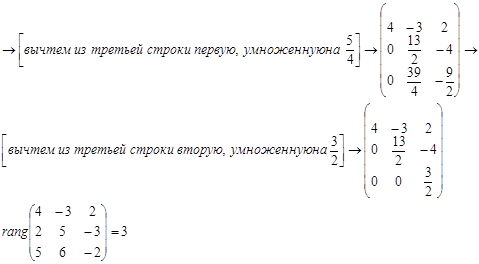
Так как ранг матрицы системы равен рангу расширенной матрицы, то система совместна.

Найдем решение системы по формулам Крамера:

Выпишем основную матрицу системы и найдем ее определитель:

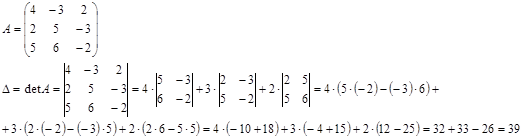
Поскольку определительный главной матрицы системы (главный определитель) не равен нулю, то система является совместной.

Подставим столбец решений в первый столбец главной матрицы и найдем ее определитель:

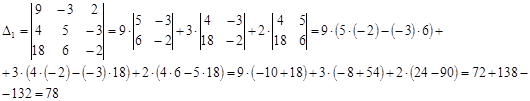
Подставим столбец решений во второй столбец главной матрицы и найдем ее определитель:

Подставим столбец решений в третий столбец главной матрицы и найдем ее определитель:

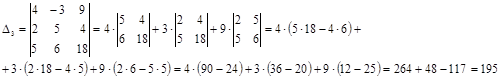
Найдем решение:

Найдем решение системы матричным способом:

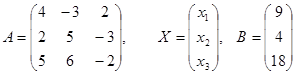
Найдем обратную матрицу. Найдем алгебраические дополнения:

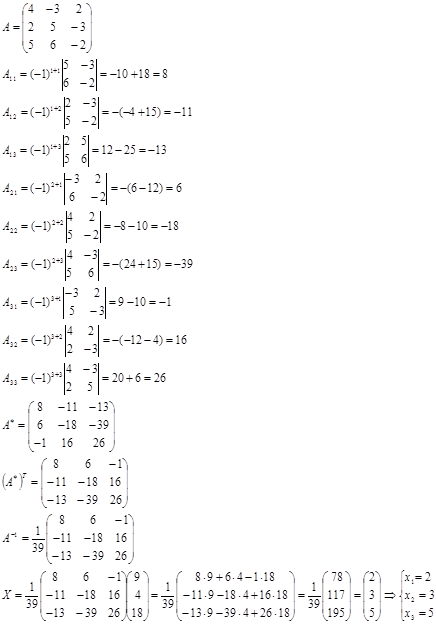
Задача 2.

Даны координаты вершин пирамиды. Средствами векторной алгебры найти:

• 1) длину ребра ;
• 2) угол между ребрами и ;
• 3) площадь грани ;
• 4) объем пирамиды ;

Решение.

Найдем длину ребра A₁A₂ по формуле.

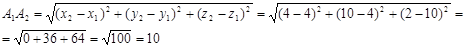
Угол б между ребрами A₁A₂ и A₁A₄ равен углу между векторами и. Найдем координаты этих векторов:

Тогда угол б определим из соотношения.

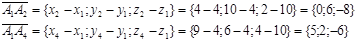
3) Найдем векторное произведение.

Векторы ,.

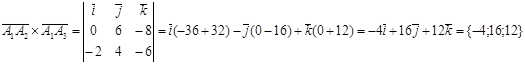
Тогда площадь грани A₁A₂A₃ равна.

4) Найдем смешанное произведение Векторы ,.

Тогда объем пирамиды:

Задача 3.

Доказать, что векторы линейно независимы и найти разложение вектора в этом базисе по векторам .

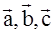
Решение.

Составим матрицу из координат векторов и найдем ее ранг. Для этого приведем ее к треугольному виду.

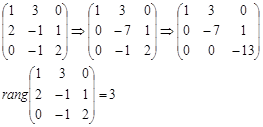
Ранг системы векторов равен 3. Векторы линейно независимы и поскольку их три и они трехмерные, то они образуют базис в трехмерном пространстве. Любой вектор пространства можно разложить по векторам этой системы.

Найдем координаты разложения. Подставим координаты векторов в последнее равенство.

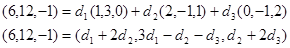
Так как векторы равны, то равны их координаты.

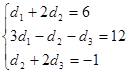
Получена система трех линейных уравнений с тремя неизвестными. Решим ее.

Разложение вектора (6, 12, -1) в данном базисе имеет вид Задача 4.

Даны три вершины треугольника: .

Найти:

• а) уравнение стороны АВ;
• б) длину стороны ВС;
• в) уравнение высоты, опущенной из вершины А;
• г) систему неравенств, определяющих треугольник АВС.

Решение.

а) уравнение стороны АВ найдем как уравнение прямой, проходящей через две точки:

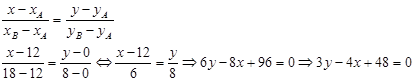
б) Длину стороны ВС найдем как расстояние между токами В и С:

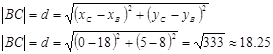
в) Высота — прямая, проходящая через точку A, перпендикулярно прямой ВС. Найдем уравнение прямой ВС и ее направляющий вектор:

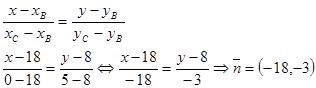
Тогда уравнение высоты:

г) Составим систему линейных неравенств, определяющих треугольник. Для определения знаков неравенств в левую часть каждого из уравнений сторон подставим координаты противоположной вершины, которая гарантированно принадлежит соответствующей полуплоскости.

Уравнения сторон:

Подставим точку С (0; 5) в уравнение стороны АВ:

Подставим точку B (18; 8) в уравнение стороны АC:

Подставим точку A (12; 0) в уравнение стороны BC:

Итак, запишем искомую систему неравенств:

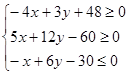
Задача 5.

Не применяя правило Лопиталя, найти пределы функций.

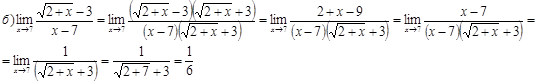
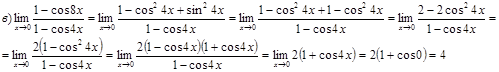
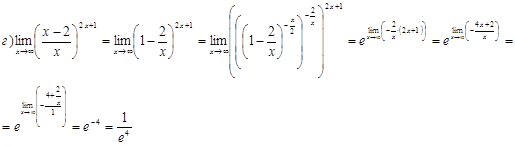
Задача 6.

Найти точки разрыва функции, если они существуют, скачок функции в каждой точке разрыва и построить график.

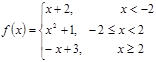
Решение.

Область определения.

Область определения кусочно-заданной функции — это объединение всех ее составляющих. Таким образом, Точки разрыва.

Очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому будем проверять граничные точки.

Исследуем на непрерывность точку х = -2.

— функция определена в данной точке Найдем односторонние пределы:

Односторонние пределы конечны и различны, значит, функция f (х) терпит разрыв первого рода со скачком в точке х = -2.

Вычислим скачок разрыва как разность правого и левого пределов:

.

т.е. график поднялся на 5 единиц вверх.

Исследуем на непрерывность точку х = 2.

— функция определена в данной точке Найдем односторонние пределы:

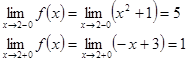
Односторонние пределы конечны и различны, значит, функция f (х) терпит разрыв первого рода со скачком в точке х = 2.

Вычислим скачок разрыва как разность правого и левого пределов:

.

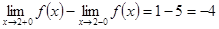
т.е. график опустился на 4 единицы вниз.

Асимптоты Асимптот нет. Есть два разрыва первого рода в точке х = -2 со скачком равным 5 и в точке х = 2 со скачком равным -4.

График.

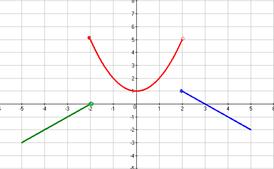
Задача 7.

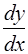
Найти производные данных функций.

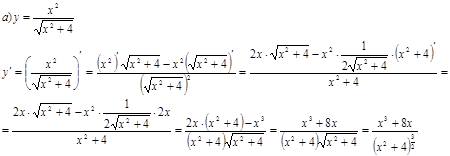
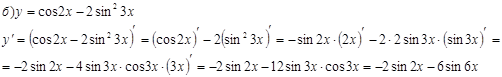
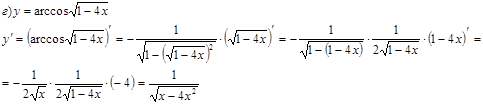
Задача 8.

Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиуса R.

Решение.

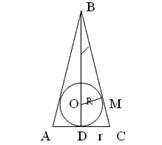
На рисунке осевое сечение конуса.

АВС — равнобедренный треугольник AB=BC;

О — центр вписанной окружности;

М — точка касания стороны ВС с окружностью;

D — точка касания основания треугольника с окужностью.

Пусть высота конуса равна х, тогда из треугольника ОВМ (прямоугольный).

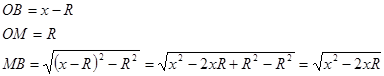
Треугольники ВСD и ВОМ подобны по двум углам, тогда справедливо равенство:

Найдем объем конуса:

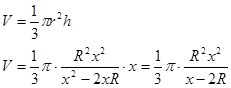
Исследуем функцию V (x) на экстремум:

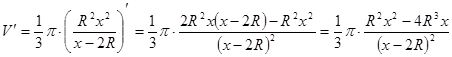
Получаем, что точка x=4R является точкой минимума. Следовательно, высота конуса наименьшего объема равна h=4R.

Радиус конуса наименьшего объема:

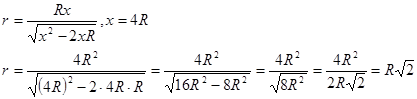
Задача 9.

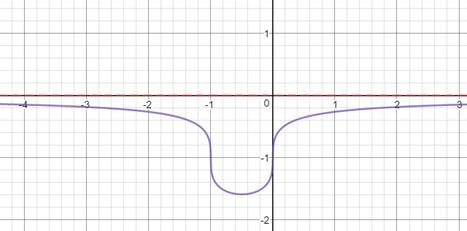
Исследовать методами дифференциального исчисления функции и построить графики:

;

Решение.

• 1) Область определения
• 2) Четность, нечетность.

Проверим, выполняется ли какое-либо из равенств:

в данном случае функция будет четной.

в данном случае функция будет нечетной.

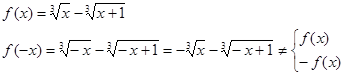
Следовательно, данная функция не является ни четной, ни нечетной. Функция общего вида.

Делаем вывод, что график функции не будет симметричен ни относительно оси Oy, ни относительно начала координат.

3) Периодичность Данная функция не является периодической.

4) Непрерывность функции.

На всей области определения данная функция является непрерывной как многочлен.

5) Точки пересечения с осями Точки пересечения с осью Ох.

Таким образом, график функции не пересекает ось Ох.

Точки пересечения с осью Оу.

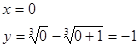
Таким образом, пересечение будет в точке (0;-1).

6) Поведение функции на концах области определения.

Концами области определения являются «-?» и «+». Найдем пределы функции при.

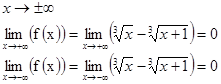
Это свидетельствует о наличии горизонтальной асимптоты у=0.

5) Критические точки функции, интервалы монотонности Для того, чтобы найти экстремумы функции, найдем производную и приравняем ее к нулю, корни этого уравнения будут критическими точками.

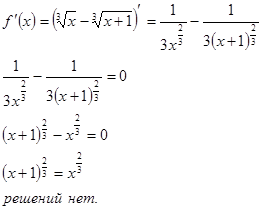
Нет точек экстремума.

6) Точки перегиба, интервалы выпуклости, вогнутости Найдем точки перегибов. Для этого необходимо найти вторую производную функции и приравнять ее к нулю. Корни полученного уравнения будут точками перегибов для указанного графика функции.

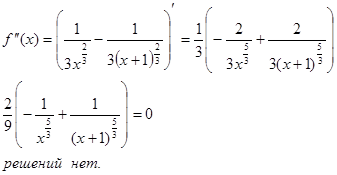
Точек перегиба нет.

7) Эскиз графика.