Расчет цифрового фильтра

Для расчета цифрового фильтра, переводящего объект из начального в конечное состояние за минимальное число периодов квантования и обеспечивающего ограничение на заданное управляющие воздействие, необходимо вычислить минимально возможный период квантования, но чтобы было удовлетворено условие:

|Um — q0|0,05, (5.1).

где Um = 1,0.

Вычисление значения q0 следует начать с определения значений коэффициентов числителя Z-передаточной функции приведенной непрерывной части для принятого периода дискретности. Пусть Z-передаточная функция приведенной непрерывной части представима в виде:

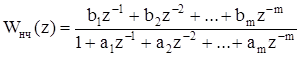
. (5.2).

Тогда Z-передаточная функция оптимального по быстродействию цифрового фильтра Wф (z) имеет вид:

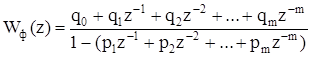
(5.3).

где pi = biq0, i = 1,2,…, m; qi = aiq0, i = 1,2,…, m;

.

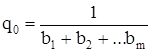
Находим функции bi, аi и Т0, используя выражение (4.7) для Wнч (z).

Для коэффициентов bi имеем:

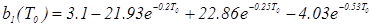
; (5.4).

;(5.5).

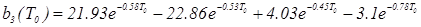
. (5.6).

Для коэффициентов аi имеем:

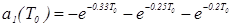
; (5.7).

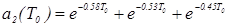
; (5.8).

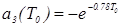
. (5.9).

Найдем выражение для q0 :

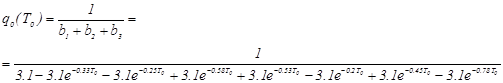
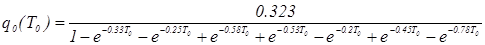
. (5.10).

Определим Т0 при котором выполняется условие (5.1), для этого построим график зависимости и изобразим его на следующем рисунке 5.1.

Рисунок 5.1 График зависимости |Um — q0(Т0)|.

При построении графика видим, что Т0 = 4,61, q0(Т0) = 1,002.

Определим коэффициенты, подставив найденное значение Т0 в выражение (5.4) и (5.5):

b1(Т0) = 0,718;

b2(Т0) = 0,332;

b3(Т0) = -0,052;

a1(Т0) = -0,932;

a2(Т0) = 0,281;

a3(Т0) = -0,027;

Подставляя найденные значения в выражения (5.2) и (5.3), определим передаточные функции приведенной непрерывной части и цифрового фильтра.

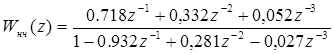
. (5.7).

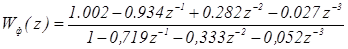
. (5.8).

Находим Z — передаточную функцию для разомкнутой цифровой системы по формуле:

Wp (z) = Wн.ч.(z) * Wф (z). (5.9).

Определим Z — преобразованную функцию замкнутой системы по каналу задание — управляюшее воздействие по формуле:

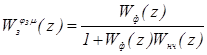
(5.10).

Определим Z — преобразованную функцию замкнутой системы по каналу задание — выходной сигнал по формуле:

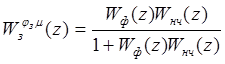
(5.10).

Пусть f — функция определяющая зависимость между q0 от Т0, т. е. q0=f (Т0), тогда f -1 — обратная ей функция, т. е. Т0=f -1(q0). Для того, чтобы найти период квантования необходимо минимизировать функцию Т0=f -1(q0) с учетом условия (5.1).

Так как в явном виде функцию Т0=f -1(q0) вывести сложно, но из графика видно, что она монотонно убывает, следовательно минимум на отрезке q0 [3,45; 3,55] будет при q0=3,55.

Расчет Т0 сводится к решению уравнения.

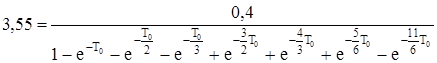
. (5.11).

Для решения данного уравнения воспользуемся алгоритмом поиска корня уравнения методом дихотомии. После решения уравнения мы получили, что Т0 =1,25.

Подставляя значение Т0 =1,25 в выражения (5.4)-(5.9) найдем коэффициенты Z-передаточной функций приведенной непрерывной части.

Тогда.

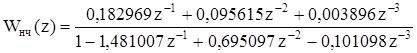
. (5.12).

При этом q0 =3,540 075. Согласно формуле (5.3).

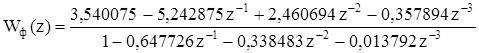
. (5.13).

Найдем Z-передаточную функцию разомкнутой цифровой системы. Она равна.

Wр (z)=Wнч (z)Wф (z) и равна.

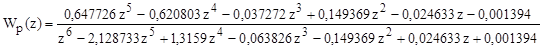
. (5.14).

Z-передаточная функция замкнутой цифровой системы по каналу задание — управляющие воздействие равна.

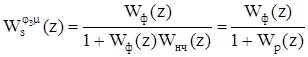
(5.15).

и равна.

.

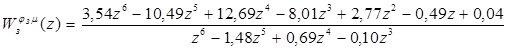
Z-передаточная функция замкнутой цифровой системы по каналу задание — выходная величина равна.

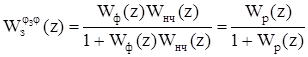
(5.16).

и равна.

.

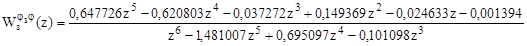
Вычислим коэффициенты усиления по указанным каналам. По определению коэффициент усиления есть отношение изменения на выходе к изменению на входе в установившемся режиме, т. е.

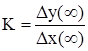
. (5.17).

Так как.

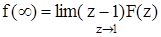
(5.18).

то подставляя выражения (5.15) и (5.16) в выражение (5.17) найдем, что ()=1, а ()=0,4. Так как x ()=1, а (0-)=0 и (0-)=0, то коэффициент усиления по каналу задание — выходная величина равен 1, а по каналу задание — управляющие воздействие равен 0,4.

Построим переходную функцию цифрового фильтра. Она равна.

.

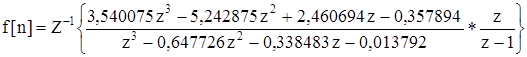
Для вычисления f[n] найдем полюса функции.

.

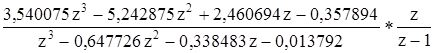
Находим 2 полюса 1-го порядка и 1 полюс 2-го порядка. Полюса 1-го порядка: z=-0,307 и z=-0,045. Полюс 2-го z=1. Для вычисления переходной функции необходимо вычислить производную следующей функции.

.

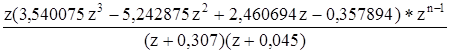
Производная данного выражения равна.

.

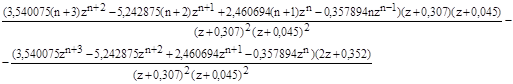
Тогда передаточная функция примет вид.

.

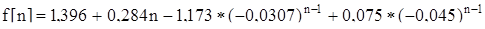
Изобразим переходный процесс на графике.

Рисунок 5.2 Переходная функция цифрового фильтра.

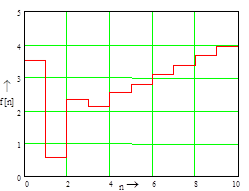
Для построения переходных процессов в замкнутой цифровой системе по каналам задание — выходная величина и задание — управляющие воздействие воспользуемся уравнениями в конечных разностях.

Суть метода заключается в следующем. Пусть передаточная функция цифровой системы.

.

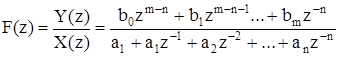
Этой передаточной функции соответствует уравнение в конечных разностях:

.

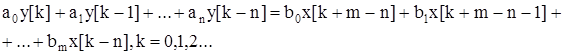
Значение искомой выходной величины равно.

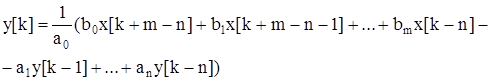
. (5.19).

Согласно формуле (5.19) получим, что переходная функция замкнутой цифровой системе по:

каналу задание — выходная величина.

y[k]=0,64 7726x[k-1] -0,62 0803x[k-2] -0,3 7272x[k-3] +0,14 9369x[k-4] -0,2 4633x[k-2] -0,1394x[k-2] +1,48 1007y[k-1] -0,69 5097y[k-2]+ +0,10 1098y[k-3];

каналу задание — управляющие воздействие.

y[k]=3,54 0075x[k] -10,48 5749x[k-1] +12,68 6121x[k-2] ;

— 8,4397x[k-3] +2,77 0507x[k-4] -0,49 7542x[k-5]+0,3 6182x[k-6]+ +1,48 1007y[k-1] -0,69 5097y[k-2]+ +0,10 1098y[k-3].

Данные расчетов были сведены в таблицы с учетом того, что x[k]=1.

Таблица 5.1 Переходная функция замкнутой цифровой системе по каналу задание — выходная величина.