Теорема Виета. 10 способов решения квадратных уравнений

ах2 + bх + с = 0, а? 0.

на 4а и последовательно имеем:

• 4а²х² + 4аbх + 4ас = 0,
• ((2ах)² + 2ах * b + b²) — b² + 4ac = 0,
• (2ax + b)² = b² — 4ac,
• 2ax + b = ± v b² — 4ac,
• 2ax = - b ± v b² — 4ac,

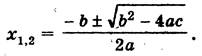
Примеры.

• а) Решим уравнение:
  • 4х² + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b² — 4ac = 7² — 4 * 4 * 3 = 49 — 48 = 1,.

D > 0, два разных корня;

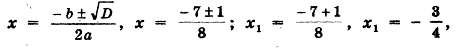
Таким образом, в случае положительного дискриминанта, т. е. при.

b² — 4ac >0, уравнение ах² + bх + с = 0 имеет два различных корня.

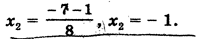
• б) Решим уравнение:
  • 4х² — 4х + 1 = 0,

а = 4, b = - 4, с = 1, D = b² — 4ac = (-4)² — 4 * 4 * 1= 16 — 16 = 0,.

D = 0, один корень;

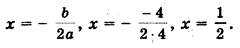
Итак, если дискриминант равен нулю, т. е.

b² — 4ac = 0, то уравнение ах² + bх + с = 0 имеет единственный корень,.

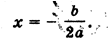
• в) Решим уравнение:
  • 2х² + 3х + 4 = 0,

а = 2, b = 3, с = 4, D = b² — 4ac = 3² — 4 * 2 * 4 = 9 — 32 = - 13, D < 0.

Данное уравнение корней не имеет.

Итак, если дискриминант отрицателен, т. е.

b² — 4ac < 0, уравнение ах² + bх + с = 0 не имеет корней.

Формула (1) корней квадратного уравнения ах² + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

4. СПОСОБ: Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид х² + px + c = 0. (1).

Его корни удовлетворяют теореме Виета, которая при, а =1 имеет вид.

x₁ x₂ = q,.

x₁ + x₂ = - p.

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.

Например,.

x² — 3x + 2 = 0; x₁ = 2 и x₂ = 1, так как q = 2 > 0 и p = - 3 < 0;

x² + 8x + 7 = 0; x₁ = - 7 и x₂ = - 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p <0, или отрицателен, если p> 0 .

Например,.

x² + 4x — 5 = 0; x₁ = - 5 и x₂ = 1, так как q= - 5 <0 и p = 4> 0;

x² — 8x — 9 = 0; x₁ = 9 и x₂ = - 1, так как q = - 9 < 0 и p = - 8 < 0.

5. СПОСОБ: Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение ах² + bх + с = 0, где, а? 0.

Умножая обе его части на а, получаем уравнение а²х² + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у² + by + ас = 0,.

равносильно данному. Его корни у₁ и у₂ найдем с помощью теоремы Виета.

Окончательно получаем х₁ = у₁/а и х₁ = у₂/а. При этом способе коэффициент, а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример.

Решим уравнение.

2х² — 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у² — 11у + 30 = 0.

Согласно теореме Виета.

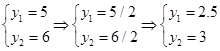
Ответ: 2,5; 3.

6. СПОСОБ: Свойства коэффициентов квадратного уравнения.

А. Пусть дано квадратное уравнение ах² + bх + с = 0, где, а? 0.

1) Если, а+ b + с = 0.

(т.е. сумма коэффициентов равна нулю), то х₁ = 1, х₂ = с/а.

Доказательство. Разделим обе части уравнения на, а? 0, получим приведенное квадратное уравнение.

x² + b/a * x + c/a = 0.

Согласно теореме Виета.

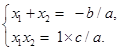
По условию, а — b + с = 0, откуда.

b = а + с. Таким образом,.

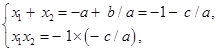
т.е. х₁ = -1 и х₂ = c/a, что м требовалось доказать.

Примеры.

• 1)Решим уравнение
• 345×2 — 137х — 208 = 0.

Решение. Так как, а + b + с = 0, то х₁ = 1, х₂ = c/a = -208/345.

Ответ: 1; -208/345.

• 2)Решим уравнение
• 132х² — 247х + 115 = 0.

Решение. Так как, а + b + с = 0 (132 — 247 + 115 = 0), то х₁ = 1, х₂ = c/a = 115/132.

Ответ: 1; 115/132.

Б. Если второй коэффициент b = 2k — четное число, то формулу корней.

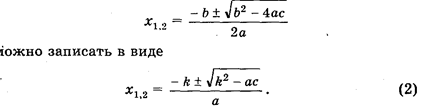
Пример.

Решим уравнение.

3х2 — 14х + 16 = 0.

Решение. Имеем:

а = 3, b = — 14, с = 16, k = — 7;

D = k² — ac = (- 7)² — 3 * 16 = 49 — 48 = 1, D > 0, два различных корня;

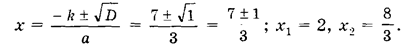
Ответ: 2; 8/3.

В. Приведенное уравнение х² + рх + q= 0.

совпадает с уравнением общего вида, в котором, а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней.

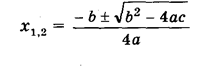
принимает вид:

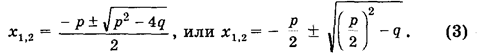
Формулу (3) особенно удобно использовать, когда р — четное число.

Пример. Решим уравнение х² — 14х — 15 = 0.

Решение.

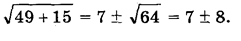
Имеем: х_1,2 =7±.

Ответ: х₁ = 15; х₂ = -1.

7. СПОСОБ: Графическое решение квадратного уравнения.

Если в уравнении х² + px + q = 0.

перенести второй и третий члены в правую часть, то получим х² = - px — q.

Построим графики зависимости у = х² и у = - px — q.

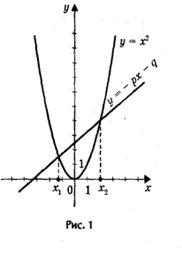
График первой зависимости — парабола, проходящая через начало координат. График второй зависимостипрямая (рис.1). Возможны следующие случаи:

— прямая и парабола могут пересекаться в двух точках,.

абсциссы точек пересечения являются корнями квадратного уравнения;

• — прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение;
• — прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.

Примеры.

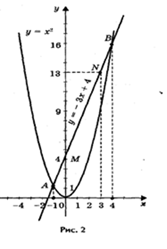
1) Решим графически уравнение х² — 3х — 4 = 0 (рис. 2).

Решение. Запишем уравнение в виде х² = 3х + 4.

Построим параболу у = х²

и прямую у = 3х + 4.

Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках, А и В с абсциссами х₁ = - 1 и х₂ = 4. Ответ: х₁ = - 1; х₂ = 4.

2) Решим графически уравнение (рис. 3).

х² — 2х + 1 = 0.

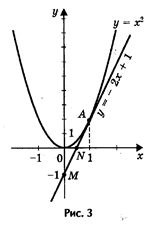
Решение. Запишем уравнение в виде х² = 2х — 1.

Построим параболу у = х² и прямую у = 2х — 1.

Прямую у = 2х — 1 построим по двум точкам М (0; - 1) и N (½; 0). Прямая и парабола пересекаются в точке, А с абсциссой х = 1. Ответ: х = 1.

3) Решим графически уравнение х² — 2х + 5 = 0 (рис. 4).

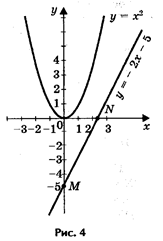
Решение. Запишем уравнение в виде х² = 5х — 5.

Построим параболу у = х² и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М (0; - 5) и N (2,5; 0). Прямая и парабола не имеют точек пересечения, т. е. данное уравнение корней не имеет.

Ответ. Уравнение х² — 2х + 5 = 0 корней не имеет.

8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Предлагаю следующий способ нахождения корней квадратного уравнения с помощью циркуля и линейки (рис. 5).

ах² + bх + с = 0.

Допустим, что искомая окружность пересекает ось абсцисс в точках В (х₁; 0) и D (х₂; 0), где х₁ и х₂ — корни уравнения ах² + bх + с = 0, и проходит через точки А (0; 1) и С (0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB * OD = OA * OC, откуда OC = OB * OD/ OA= х₁х₂/ 1 = c/a.

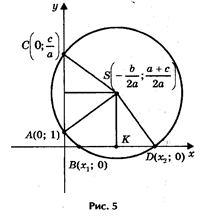
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому.

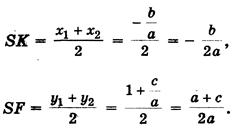
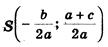
Итак:

• 1) построим точки (центр окружности) и A (0; 1);
• 2) проведем окружность с радиусом SA;
• 3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

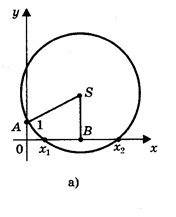
• 1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6, а) В (х₁; 0) и D (х₂; 0), где х₁ и х₂ — корни квадратного уравнения ах² + bх + с = 0.
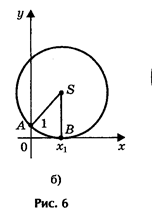
• 2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6, б) в точке В (х₁; 0), где х₁ — корень квадратного уравнения.

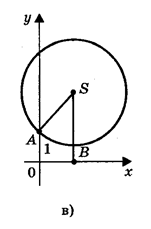
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис. 6,в), в этом случае уравнение не имеет решения.

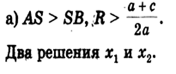
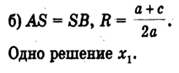
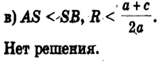
Пример.

Решим уравнение х² — 2х — 3 = 0 (рис. 7).

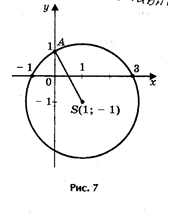
Решение. Определим координаты точки центра окружности по формулам:

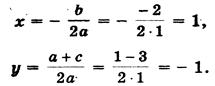
Проведем окружность радиуса SA, где, А (0; 1).

Ответ: х₁ = - 1; х₂ = 3.

9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.

Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с. 83 (см. Брадис В. М. Четырехзначные математические таблицы. — М., Просвещение, 1990).

Таблица XXII. Номограмма для решения уравнения z² + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

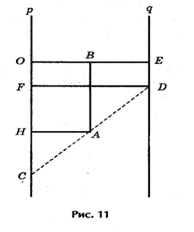
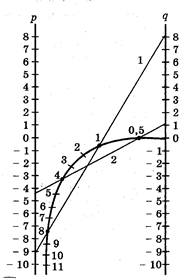
Криволинейная шкала номограммы построена по формулам (рис.11):

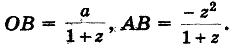
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию.

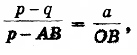
откуда после подстановок и упрощений вытекает уравнение.

z² + pz + q = 0,.

причем буква z означает метку любой точки криволинейной шкалы.

Примеры.

1)Для уравнения.

z2 — 9z + 8 = 0.

номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис.12).

• 2) Решим с помощью номограммы уравнение
• 2z² — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение.

z² — 4,5z + 1 = 0.

Номограмма дает корни z₁ = 4 и z₂ = 0,5.

3) Для уравнения.

z² — 25z + 66 = 0.

коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение.

t² — 5t + 2,64 = 0,.

которое решаем посредством номограммы и получим t₁ = 0,6 и t₂ = 4,4, откуда z₁ = 5t₁ = 3,0 и z₂ = 5t₂ = 22,0.

10. СПОСОБ: Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

Примеры.

1) Решим уравнение х2 + 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис.15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.

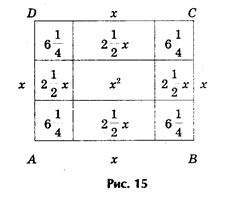
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х², четырех прямоугольников (4* 2,5х = 10х) и четырех пристроенных квадратов (6,25* 4 = 25), т. е.

S = х² + 10х + 25. Заменяя х² + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим.

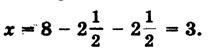
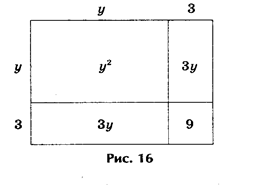
2) А вот, например, как древние греки решали уравнение у² + 6у — 16 = 0.

Решение представлено на рис. 16, где у² + 6у = 16, или у² + 6у + 9 = 16 + 9.

Решение. Выражения у² + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у² + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = - 8 (рис.16).

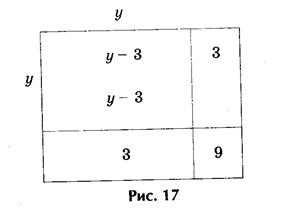
3) Решить геометрически уравнение у² — 6у — 16 = 0.

Преобразуя уравнение, получаем у2 — 6у = 16.

На рис. 17 находим «изображения» выражения у² — 6у, т. е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у² — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у² — 6у равным ему числом 16, получаем: (у — 3)² = 16 + 9, т. е. у — 3 = ± v25, или у — 3 = ± 5, где у₁ = 8 и у₂ = - 2.