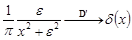Финитные функции. 
Основные понятия векторного анализа

Функция называется финитной, если она обращается в 0 вне некоторого отрезка.

Пусть есть множество финитных и бесконечно дифференцируемых на? функций. Очевидно, что есть линейное пространство.

Будем говорить, что последовательность функций, , при любом ?, сходится к функции, если выполнены следующие условия:

1) носители всех функций, , лежат на некотором отрезке :

?,.

2) при любом? последовательность производных равномерно на сходится к: .

Обозначается: при .

Пространство обобщенных функций

Линейное пространство с введенной выше сходимостью называется пространством основных функций.

Покажем, что функция.

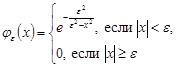
принадлежит пространству.

Действительно, односторонние производные всех порядков справа и слева в точках и равны нулю. Поэтому функция бесконечно дифференцируема на всей числовой оси. При этом — финитная, так как. Значит,. На рисунке 3.23 изображена данная функция при различных .

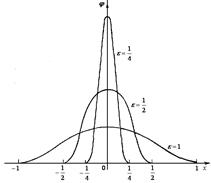
Рисунок 3.23 — График функции.

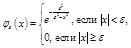
Обобщенной функцией? называется функция, для которой выполнены следующие условия:

• 1) каждой функции сопоставляется число ;
• 2) для любых двух чисел, и любых двух функций, выполнено равенство

;

3) из при следует, что.

при .

Множество всех обобщенных функций обозначается через. Множество является линейным пространством, так как.

.

В пространстве выделяется класс регулярных обобщенных функций: функция абсолютно интегрируема на любом конечном отрезке и справедливо равенство:

.

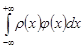
Обобщенные функции также называются распределениями, так как плотность распределения вещества неизмерима никаким прибором и представляет собой интеграл .

Обобщенные функции, не являющиеся регулярными, называются сингулярными.

Например, -функция, определяемая по правилу является сингулярной обобщенной функцией.

В самом деле, линейность и непрерывность очевидны. Докажем его сингулярность. Предположим, что она является регулярной обобщенной функцией. Тогда существует такая интегрируемая функция, что.

.

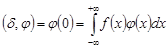
В частности, это равенство должно быть выполнено для функции, определенной равенством.

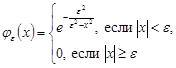
при любом .

Поэтому.

.

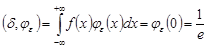
С другой стороны, подберем такое, что.

.

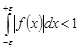
Поскольку, то получаем.

.

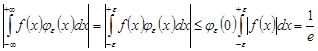
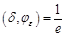
что противоречит равенству .

Противоречие доказывает, чтофункция является сингулярной функцией.

Будем говорить, что последовательность, где, сходится к, если для любой функции выполнено равенство.

при .

Обозначается:

Такая сходимость называется слабой сходимостью.

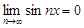
Пример. Докажем, что в пространстве. Каждая функция из пространства основных функций абсолютно дифференцируема на всей числовой оси. Тогда.

.

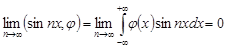
Иногда вместо последовательности обобщенных функций рассматриваются функции, зависящие от параметра. В этом случае запись при означает, что.

.

В частности, запись при означает, что.

.

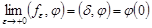
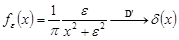
Пример. Докажем, что при. Очевидно, что функции порождают регулярные функции в. Возьмем любую функцию. Пусть ее носитель лежит на отрезке. Тогда.

.

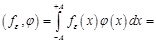
Так как функция дифференцируема и финитна на ?, то, применяя формулу конечных приращений Лагранжа, получаем неравенство:

.

Поскольку.

.

.

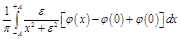
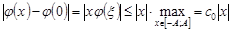
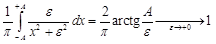
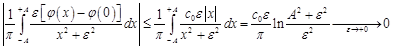
то получим.

.

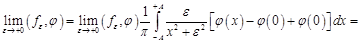
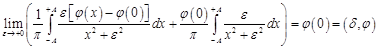
Согласно определению это означает, что .